
Immunoglobulin domain 8fab |

Zinc finger 1zaa |

Eukaryotic protein kinase domain 1apm |

EGF-like domain 1apo |

WD domain 1gp2 |
EF hand 1osa |
Keywords: models in biochemistry, protein domain evolution, neural networks, ethics of modeling.
New domain functions evolve within the constraints of maintaining thermodynamic
stability and autonomous folding capability. This gives rise to a complex
interplay of molecular organization and evolutionary dynamics, which is
still a largely unexplored area of research. My aim in the present paper
is to approach this problem from a perspective informed by recent developments
in complexity theory. This work employs distributed representation by neural
networks in building relational models of protein domain evolution. I will
also address the explicit ethical dimension inherent in choosing and developing
models in biomedical science. Ethical implications of developing complex
systems models of biomolecules are discussed on this premise.

Immunoglobulin domain 8fab |

Zinc finger 1zaa |

Eukaryotic protein kinase domain 1apm |

EGF-like domain 1apo |

WD domain 1gp2 |

EF hand 1osa |
(1) Complex systems consist of a large number of elements. At the atom level, protein domains typically consist of thousands of elements. At a higher level of description, the amino acid level, they are comprised of up to several hundred elements. Whilst description and modeling at the atom level is computationally intractable at present, domain systems can be modeled at the amino acid level.
Please note that, for reasons that will become clear when neural network modeling of domain evolution is discussed below, the positions along the protein sequence, rather than the amino acids themselves, are defined as the elements of the systems. These elements can be in one of 20 different states (be filled by one of the 20 amino acids). The state of an element can change, i.e., a positions can mutate to a different amino acid.
(2) The elements of a complex system interact in a dynamic fashion and these interactions change over time. Dynamic interactions between amino acids (positions in certain states) mediate the folding process and a stable pattern of interactions subsequently determines the three-dimensional fold of the domain. Dynamic interactions are also fundamental to domain functions that are mediated by conformational changes. During evolution, the pattern of interactions between fold positions changes as a consequence of amino acid substitutions (gain or loss of hydrogen bonds, salt bridges, or van der Waals interactions).
(3) The interactions between elements are richly connected – any one element influences, and is influenced by, a large number of others. In a domain fold, amino acid positions along the linear protein sequence are engaged in multiple local (involving positions that are close in the linear sequence) and non-local (involving positions that are distant in the linear sequence) physical interactions. With the exception of neutral positions, each fold position makes an individual fitness contribution and simultaneously affects the fitness of many other positions within the domain. Fitness is here defined as the capacity of the domain to maintain its structural integrity and to carry out specific function(s).
(4) The interactions between elements are non-linear. Small causes can have large results, and vice versa. Complexity results from the patterns of richly connected interactions between the elements.Complex systems exhibit so-called emergent properties, properties that are only seen in systems of an equivalent degree of complexity. In other words, the behavior of complex systems cannot be derived on the basis of knowledge of their parts. One of the key processes responsible for emergence is self-organization (Cilliers 1998, p. 89; Holland 1998, pp. 115, 225). This co-ordinated behavior results from the non-linear interactions of its components which leads to collective effects. Self-organization also leads to spontaneous transitions into new collective states, at times as adaptive responses to changes in their environment.
The non-linearity of interactions between amino acid positions is a major reason why certain amino acid substitutions at only one or a few positions may unravel a domain fold. And, conversely, is a reason why amino acid sequences can at times diverge from homologous sequences beyond any statistically significant similarity, while the shared domain fold is still conserved intact. We are unable to explain or predict these phenomena (at least for now), and so they also illustrate how non-linearity severely limits predictability. Another related issue is the persistent elusiveness of a solution to the ‘folding problem’, despite three decades of intense efforts.
(5) The interactions between elements are relatively short-range. Physical constraints and information are mostly transmitted between immediate neighbors. However, this does not mean that there can not be long-range influences. In a richly connected network, the path between two elements can usually be covered in a small number of steps. Influences can be enhanced, suppressed, or modulated in some way along the path. Amino acids in domain cores are packed in an engergetically favorable arrangement, and strong local constraints on amino acid variation are present. The network of amino acids that are in contact with each other collectively constrains mutational change. Although this mechanism is mediated by local interactions, it can propagate throughout the domain to distant sites via "chains of local interactions" (Lapedes et al. 1997). Non-linear constraint modulation along such interaction chains occurs due to the rich connectivity between elements (multiple physical interactions and mutual constraints).
(6) There are recurrent interaction pathways. The effects of a state change at one element can feed back on itself, either directly or via a number of intervening states. The feedback can be either enhancing or inhibiting. Depending on its nature, a mutation (state change) at one domain position may enhance or inhibit the probability of a particular amino acid substitution (after selection) at coevolving positions. These subsequent mutations may in turn enhance or inhibit further change at the first position.
(7) Complex systems have a history. They evolve through time, and their present state is constrained by their past. Present-day protein domains have evolved from ancestral domains. Domain evolution can only occur within the constraints of maintaining thermodynamic stability and autonomous folding capability.
(8) It can be difficult to precisely delineate the boundaries of a complex system. Boundary definitions are often derived for descriptive purposes and are influenced by the position of the observer. Molecular biology in general follows a top-down approach. Bodies are broken down into tissues, tissues into cells, and cells into molecules, biochemical compounds, and atoms. Reductionism then seeks to explain the functioning of the organism on the basis of the chemistry and physics of its constituent parts. Complexity theory asserts the importance of balancing an analytical top-down approach, indispensable for the identification of the building-blocks of a system, with a bottom-up approach, in order to study how living systems emerge from the laws of physics and chemistry. Whilst all biological processes are consistent with the physical and chemical laws of our universe, and in this sense can ultimately be ‘reduced’ to chemistry and physics, there is a growing awareness among scientists that biological phenomena require an approach that equally addresses the problem of emergence. Emergent phenomena result from the complex, rule-governed, interactions of a large number of biomolecules, in a highly context-dependent manner. Consciousness, to mention a familiar example, arises out of the unimaginably densely connected interactions of billions of neurons, and is not a property of any one brain region, let alone of the neurons themselves. Consciousness is an emergent property of the brain as a whole.
From a different perspective, one which pays close attention to process
and interaction across multiple levels of biological complexity, the living
world appears as a multidimensional whole of complex systems within complex
systems. The demarcation lines between different levels of organizational
complexity, and the delineation of any one of these systems, rest on boundaries
defined according to criteria that will always, to some extent, be contingent
on the perspective of the observer. This notwithstanding, the discussion
so far has shown that protein domains can legitimately be seen as complex
systems in their own right, far down in a nested hierarchy of proteins,
protein complexes, structural and functional networks in cells, whole cells
and organisms.
Steroid, thyroid and retinoid hormones comprise the broadest class of gene-regulatory ligands known. Their receptors belong to the diverse superfamily of nuclear receptors (NRs) that are present in all metazoans from cniderians onward and have had a central part in the evolution of biological complexity since the Cambrian explosion (Escriva et al. 1997, Laudet et al. 1992). As ligand-inducible transcription factors, NRs play essential roles in the regulatory pathways that transmit signals, originating from the extra- and intra-cellular environment, to large genetic networks through a complex sequence of molecular interactions. These genetic networks regulate many aspects of development and function; specifically, higher morphology, the immune system, the nervous system, as well as reproductive and metabolic systems.
The ligand-binding domain of nuclear receptors possesses a unique fold that is partly disordered in the absence of ligand, termed the "antiparallel a helical sandwich" (for refs., see Nagl et al. 1999). The helices are grouped into three layers around an internal ligand-binding core. Crystallographic studies of ligand-bound NRs suggest a structural role for ligand that is fundamental to the allosteric control mechanisms found in the ligand-binding domain. The ligand is completely buried within the domain interior and contributes to the hydrophobic core of the active conformation of the NR. Therefore, ligand binding directs the alignment of the secondary structural elements critical for receptor function, and strongly constrains the conformational freedom of the ligand-binding domain.
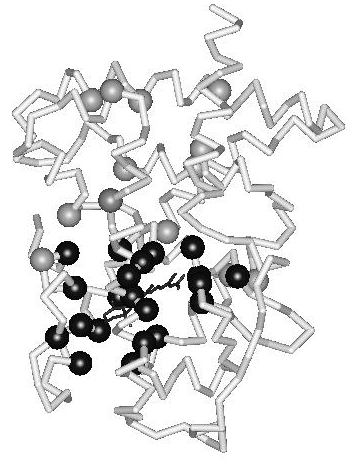
During the evolution of the NR superfamily, the ligand-binding pocket has evolved to allow binding of ligands possessing strikingly diverse chemical structures. Escriva et al. (1997) proposed that the ancestor of the superfamily was an orphan receptor without ligand-binding capability. Their study of NR evolution suggests that liganded receptors have arisen relatively recently and have gained the ability to bind ligands independently. Since the ligand-contacting residues line the binding pocket in the domain core, they perform a dual role; a functional role in ligand recognition and a structural role as core residues. With respect to ligand recognition, they can be seen to constitute an ‘interior interaction surface’. In principle, this would allow great scope for the evolution of the ligand-binding pocket. However, since the hydrophobic ligand is an integral part of the domain core in the active conformation, the ligand and the ligand-binding residues combined need to be able to maintain structural stability and domain dynamics (conformational changes). How is this potential conflict between structural constraints and functional diversity resolved within the domain fold? In an earlier study, it was shown that the ligand-contacting residues in the hormone-binding pocket are evolutionarily linked to an extensive, hierarchically organized, network of coevolving positions (Fig. 2) (Nagl et al. 1999). The nature of the mutations in correlated positions suggests that they compensate for the destabilization resulting from the binding of diverse ligands and preserve the structural integrity and the conformational dynamics of the ligand-binding domain. In conclusion, a distributed evolutionary mechanism, involving the domain fold as a whole, is present in the ligand-binding domains of nuclear hormone receptors. It is suggested that this mechanism maintains a thermodynamically favorable interplay between molecular organization and evolutionary dynamics.
In this work, where protein domains are studied as complex adaptive systems, the positions along the linear amino acid sequence of the domain are conceptualized as the elements, or ‘agents’, of the system that can each assume one of 20 different states (i.e., the 20 amino acids) (Fig. 3). Four classes of fold positions can be distinguished in domains that are descended from a common ancestral domain: (i) positions with conserved amino acid identities; (ii) positions with conserved physicochemical properties; (iii) positions with variable physicochemical properties (often belonging to the distributed network of coevolving positions (see Sect. 2); and (iv), unconstrained positions accumulating neutral mutations. Positions in the coevolutionary distributed network to be modeled by neural networks belong to class (ii) or (iii).
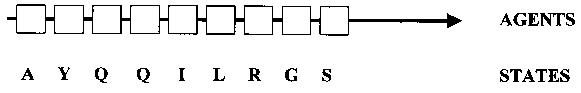
| H(i) = - ås P(si) log P(si) | (1) |
Mutual information is defined in terms of entropies involving the joint
probability distribution, P(si,
s’j),
of occurrence of symbol s at position i, and s’ at
position j. The associated entropies for each position i
and j are
| H(i) = - åsi P(si) log P(si) | (2) | |
| H(j) = - ås’j P(s’j) log P(s’j) | (3) |
And the joint entropy is defined as
| H(i, j) = - åsi, s’j P(si, s’j) log P(si, s’j) | (4) |
The mutual information, M(i, j), is defined as
| M(i, j) = H(i) + H(j) -H(i, j) | (5) |
If the positions are independent, their mutual information is 0. If, on the other hand, the positions are correlated, their mutual information is positive and achieves its maximum value if there is complete covariation.
Given a set of sequences that are assumed to be independent and identically
distributed samples from a probability distribution, one can independently
estimate each pairwise probability distribution for every pair of positions
by frequency counting. However, sequences belonging to a domain family
are not independent samples, but are related through shared ancestry described
by a phylogenetic tree. If two mutations occur independently in an ancestral
sequence and these are subsequently inherited by many of the descendants
further down the tree, the two positions involved will receive a high mutual
information score. To estimate the mutual information content between position
pairs that is created by tree inheritance alone, and not by covariation,
a simulation experiment can be performed (Nagl
et
al. 1999, Lapedes et al.
1997). This procedure simulates the evolution of sequences by random mutations
along a phylogenetic tree obtained from the domain sequence alignment.
Using the outgroup as a seed, random sequences are evolved following the
phylogenetic tree obtained from the real data set. During simulated random
mutation of sequences, the states of the sequences are duplicated at a
bifurcation point in the tree, and the two copies are then independently
evolved. Every amino acid can mutate with equal probability to any other
amino acid. The procedure is repeated numerous times, and significance
threshold values are determined from the frequency distributions of the
mutual information scores in the control and real data sets. Any mutual
information score greater than the lower boundary value, has a low probability
of being caused by inheritance through the tree.
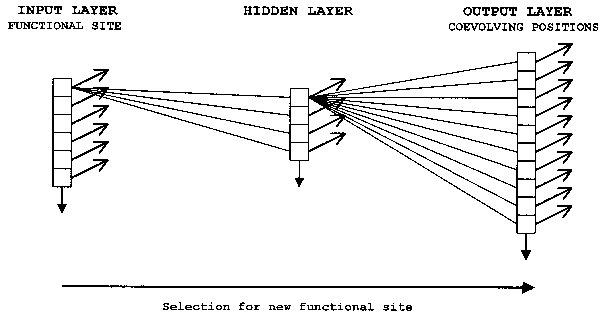
ANNs are computer algorithms that attempt to model the way the brain works and draw on the analogies of adaptive biological learning. One particularly valuable and intriguing characteristic of information processing in biological brains seems to be also present in ANNs – the ability to make decisions based on very complex, noisy, irrelevant and/or partial information. While the comparison with the human brain has led to some exaggerated claims concerning ANNs, this analogy is a very useful way to describe the construction and function of neural nets. An ANN is composed of a large number of highly interconnected processing elements that are analogous to neurons and are tied together with weighted connections that are analogous to synapses. Interconnected neurons, whether biological or artificial, have certain neuro-‘logical’ properties and can be seen as logic gates: They receive input signals from a large number of other neurons, process these signals according to specified transformation functions, and produce an output signal as a result of this processing. Brains and artificial neural networks represent information in a distributed fashion; information is encoded by the patterns of synaptic connection strengths (weights) between neurons. The distributed networks of neurons perform many transformation steps in parallel, a style of computation known as parallel distributed processing (PDP). When fully connected neural networks are used, a combination of a large set of connection weights and nonlinear transfer functions allows models of any complexity to be fitted between the response and the input parameters. Neural networks are therefore highly efficient nonlinear data modeling devices, and can be seen as universal models for information processing in complex system. Arguably, the evolution of functional sites within the coevolutionary network of a domain family can be conceptualized as a type of PDP (Fig. 4). It should be well noted that this statement is not meant to imply a direct correspondence in architecture between the coevolutionary network and an ANN, but refers to an analogous information-processing mode. Furthermore, as all parallel-distributed computational steps are executed simultaneously, ANN models of domain evolution do not represent the historical sequence of step-wise mutation at coevolving sites over evolutionary time. This temporal aspect of coevolutionary networks can be analyzed and modeled by reconstruction of ancestral states by parsimony.
For the purpose of building an ANN model of a coevolutionary network, we return to our previous representation of a protein as a chain of agents in a linear sequence, each of which can take on one of 20 states (amino acids) (Fig. 3). The agents are understood as mechanisms for mediating interactions (Holland 1998, p. 6), and state transitions in agents (mutations) lead to a modification in the patterns of interactions, sometimes resulting in a change in structure/function. The state transitions are constrained by rules (Holland 1998, p. 116), and all possible state sequences are the outcomes of a succession of transitions specified by these rules. In this way, the rules generate evolutionary novelty. Structure/function can now be re-conceptualized as an emergent property, the result of context-dependent interactions, that changes over time.
It is possible to encode the state transition rules in the values of the connection weights of an ANN model of the coevolutionary network. Specifically, the evolution of new functional sites within the coevolutionary network can be modeled by a classical fully-connected feedforward neural network (Fig. 4) (for a detailed mathematical treatment of feedforward network properties and behavior, see, for example, Skapura 1995, Mehrotra et al. 1996, Livingstone et al. 1997).
An important decision to be made concerns how to encode the states of the agents. To name just two alternatives, they can be encoded as binary vectors (bitstrings), or as vectors of real numbers (any value between -1 and 1), depending on which aspect of the states we wish to model. If we want to encode amino acid identities (A, W, S, D, etc.), bitstring encoding and a discrete ANN model suggest themselves as the most appropriate choice. If we want to encode information about certain physicochemical properties of the amino acids (hydrophobicity, hydrophilicity, charge, polarity, volume, etc.), this can be achieved by using real number vectors, where each property is expressed by a normalized value between -1 and 1, and a continuous ANN model.
The Hippocratic oath expresses a duty of nonmaleficence, or not inflicting harm, together with a duty of beneficence, or doing good (Beauchamp & Childress 1989, p. 120). These duties are absolutely fundamental to biomedical ethics and the practice of medicine. In contemporary medicine, biomedical research scientists are doctors’ close partners, and thus it can be argued that the ethical prescriptions of the Hippocratic oath ought to extend to their branch of the life sciences. Scientists’ duties may be loosely phrased as follows: "I will pursue my scientific work to help the sick according to my ability and (best) judgement, but I will never use it to injure or harm them."
In the light of the immeasurable potential benefits of artificially designed proteins in molecular medicine, it is greatly desirable that we develop a repertoire of design methods that would enable us to create proteins for therapeutic uses. Thus, one can assert that a duty to develop such techniques exists, and that this duty derives from the principle of beneficence. However, many problems still hamper the attainment of these goals. On the one hand, it has been recognized for some time that protein design can draw vital insights from evolutionary principles. On the other hand, the complex interplay of molecular organization and evolutionary dynamics is still poorly understood, and this lack of understanding presently limits potentially extremely fruitful evolutionary approaches to protein design. An awareness of these problems, together with the insight that proteins are complex adaptive systems – in other words, that they evolve as complex systems – leads to a duty to study their complex systems properties. Such a duty is grounded in the reasonable expectation that such a research program will enable the gain of new knowledge, and the development of new design techniques, that are inaccessible from within other conceptual frameworks. This duty therefore also follows from the principle of beneficence. The work on complex systems models of protein domain evolution presented in this paper was carried out in the hope that it will help elucidate how new functions evolve in stable folding architectures, and be a contribution towards overcoming the current limitations in protein design.
Whenever there are consequences to human welfare, the duty to treat complex systems as complex systems is also grounded in the principle of nonmaleficence, or not inflicting harm. This is quite immediately obvious in the case of large complex systems, such as ecosystems or whole biological organisms. An environmental risk assessment, or a drug trial, that employs models that are inadequate for detecting effects due to complex systems properties, may pose great risks to people. A duty to avoid the use of such models, and to develop alternatives that can model complex systems behavior, can be easily appreciated. It may, however, at first be less obvious how such a duty due to nonmaleficence could be postulated for models of much smaller complex systems, models of proteins for example.
Here, we need to briefly digress to consider that models are in a certain sense metaphorical constructions (Nagl 1998;Holland 1998, p. 207). As such, they carry with them not only explicit messages but also implicit content. A model is a device for seeing the world in a particular way. A well-developed scientific model accumulates a complicated assortment of techniques, interpretations, standards of proof, and so on; and may well have a cognitive impact far transcending the original context in which it was conceived. Much of this remains unwritten, but is understood by everyone who has been socialized within the research tradition associated with the model.
Importantly, models shape our habits of thought. It seems therefore unwise to think that, while we may feel an ethical obligation to develop models that embody the complexities of the human body, we may ‘get away’ with ignoring the complex systems properties of biomolecules. Our fundamental orientation toward life is always at issue, no matter what part of it we happen to focus on at the time. Habits of thought that prompt us to take heed of the complexity inherent in all biological entities, will direct our thinking away from seeing and representing such entities in simplistic terms – away from mechanistic conceptions of molecules or visions of machine-like bodies. They will hopefully also stop us from intervening in the human body from this fragmented, and potentially extremely harmful, perspective. It is within this wider context that nonmaleficence can be seen as a guiding principle, supporting the duty to study the complex systems properties of biological entities. On the positive side, these novel habits of thought may direct us toward an understanding of the world as a multidimensional whole of complex systems within complex systems. Such a change in thinking may subsequently lead to new biomolecular therapies that seek to cooperate with, rather than control, living systems. The central role of biomolecules in molecular medicine, a tremendously powerful and influential new research field, may make complex systems models of these molecules instrumental in bringing about such a global change in scientific attitude.
This leads on to some final points I wish to make. My reflections on
ethical issues of model choice find an echo in Longino’s work on theoretical
virtues (Longino 1996, p. 44). These virtues complement the cognitive values
of accuracy, consistency, simplicity, breadth of scope and fruitfulness,
that are commonly applied to assess the merits of scientific models. Longino’s
virtues of ‘novelty’ and ‘mutuality of interaction’ are especially pertinent
to my concerns. Longino defines ‘novelty’ as models or theories that differ
in significant ways from presently accepted ones by (i) attempting to elucidate
phenomena that have not been previously studied, (ii) postulating different
processes, (iii) adopting different principles of explanation, and (iv),
incorporating alternative metaphors (p. 45). As Longino (1996) states,
"treating novelty as a virtue reflects a deep skepticism that mainstream
theoretical frameworks could be adequate to the problems confronting us"
(p. 46). It is certainly from a great disquiet regarding the present state
of our biomedical models that I argue for an urgent need for complex systems
models, which can be seen to fulfil all four of Longino’s criteria of novelty.
Finally, the virtue of ‘mutuality of interaction’ values theories and models
that treat relationships between entities and processes as mutual, avoid
causal explanations based on single factors, and take complex interaction
as a fundamental principle of explanation (Longono 1996, p. 47). Clearly,
complex systems models are embodiments of this virtue par excellence.
In conclusion, complex systems approaches, informed by the theoretical
virtues of ‘novelty’ and ‘mutuality of interaction’, are highly relevant
to current biomedical research, if one is to fulfil the duties of the Hippocratic
oath.
Cilliers, P: 1998, Complexity & Postmodernism, Routledge, London.
Escriva, H.; Safi, R.; Hanni, C.; Langlois, M.-C.; Saumitou-Laprade, P.; Stehelin, D.; Capron, A.; Pierce, R.; Laudet, V.: 1997, ‘Ligand binding was aquired during evolution of nuclear receptors’, Proceedings of the National Academy of Sciences USA, 94, 6803-8.
Gerstein, M.; Sonnhammer, E.L.; Chothia, C.: 1994, ‘Volume changes in protein evolution’, Journal of Molecular Biology, 236, 1067-78.
Hacking, I.: 1983, Representing and Intervening, Cambridge Univ. Pr., Cambridge.
Holland, J.H.: 1998, Emergence, Addison-Wesley, Reading/MA.
Keller, E.F.: 1992, Secrets of Life, Secrets of Death, Routledge, London.
Korber, B.T.M.; Farber, R.M.; Wolpert, D.H.; Lapedes, A.S.: 1993. ‘Covariation of mutations in the V3 loop of human immunodeficiency virus type 1 envelope protein: An information theoretic analysis’, Proceedings of the National Academy of Sciences USA, 90, 7176-80.
Laudet, V.; Hanni, C.; Coll, J.; Catzeflis, F.; Stehelin, D.: 1992, ‘Evolution of the nuclear receptor gene superfamily’, EMBO Journal, 11, 1003-13.
Lapedes, A.S.; Giraud, B.G.; Liu, L.C.; Stormo, G.D.: 1997, ‘Correlated Mutations in Protein Sequences: Phylogenetic and Structural Effects’, AMS/SIAM Conference on Statistics in Molecular Biology, Seattle/WA.
Livingstone, D.J.; Manallack, D.T.;Tetko, I.V.: 1997, ‘Data modelling with neural networks: Advantages and limitations’, Journal of Computer-Aided Molecular Design, 11, 135-42.
Longino, H.E.: 1996, ‘Cognitive and non-cognitive values in science: Rethinking the dichotomy’, in: L. Hankinson and J. Nelson (eds.), Feminism, Science, and the Philosophy of Science, Kluwer Academic Publishers, London, pp. 39-58.
Mehrotra, K.; Mohan, C.K.; Ranka, S.: 1996, Elements of Artificial Neural Networks, MIT Press, Cambridge/MA.
Nagl, S.B.: 1998, ‘Genetic essentialism and the discursive subject’, Proceedings of the 20th World Congress of Philosophy, August 1998, Boston/MA [a full-text version is available at http://www.bu.edu/wcp/Papers/Bioe/BioeNagl.htm].
Nagl, S.B.; Freeman, J.; Smith, T.F.: 1999, ‘Evolutionary constraint networks in ligand-binding domains: an information-theoretic approach’, Proceedings of the Pacific Symposium on Biocomputing 1999, 90-101 [a full-text version is available at http://www-smi.stanford.edu/projects/helix/psb99/].
Skapura, D.M.: 1995, Building Neural Networks, Addison Wesley,
Reading/MA.
Copyright Ó 2000 by HYLE and Sylvia Nagl