HYLE – An International Journal for the Philosophy of Chemistry, Vol. 6 (2000), No. 2, pp.161-173
Copyright Ó 2000 by HYLE and F. Michael Akeroyd

Why was a Fuzzy Model so Successful in Physical Organic Chemistry?

F. Michael Akeroyd*

Abstract: This paper examines a facet of the rise of the Hughes-Ingold Theory of Nucleophilic Substitution in Organic Chemistry 1933-1942, arguing that the S_N1/S_N2 model of reaction mechanism used by Hughes and Ingold is an example of a fuzzy model. Many real world ‘Fuzzy Logic’ Controlling Devices gave better results compared to classical logic controlling devices in the period 1975-1985. I propose that the adoption of fuzzy principles in the Hughes-Ingold program 1933-1940 led to scientific advance at a time when the rival programs, based on classical principles, had stalled owing to problems associated with the fuzziness of the data. I suggest also that there is an analogy between the success of second generation fuzzy logic controllers 1985-95 and the success of the successor Winstein model from 1956 onwards.

Keywords: fuzzy logic, fuzzy model, possibilistic reasoning, physical organic chemistry, reaction mechanism.

1. Introduction

The development of attempts to build satisfactory models for the mechanism of organic chemistry nucleophilic substitution reactions 1930-1970 is the theme of the present article. I claim that many of the developments in the field of Fuzzy Logic post 1965 are relevant to the original Hughes-Ingold model of nucleophilic substitution at saturated carbon atoms. A fuzzy set is one in which the boundaries are not sharp and degrees of membership are allowed, whereas a crisp set is one in which boundaries are sharply defined and membership is an all-or-nothing affair. A simple chemical example would be the classification of substances into either acids or bases (with a ‘fuzzy’ overlap region for substances both weakly acidic and weakly basic) or into acids/amphoteres/bases (crisp). In the fuzzy system there is no separate class for the amphoteres (which can exhibit both acidic and basic characteristics): amphoteric examples are classed as both basic and acidic (i.e. simultaneously members of both sets, simultaneously both true and false in classical logical terms) whereas in the crisp classification a new set is created and inserted between the acids and bases with sharp boundaries between all three (see e.g. Chang 1998).

Classification along fuzzy lines as opposed to crisp lines possesses both advantages and disadvantages: in this account we will focus on the advantages. For example, is it meaningful to suggest that there is some different essence in the class of amphoteres that makes them sharply distinctive from both the acids and the bases? Under forcing conditions even the strong base OH^- can donate a proton to another base thus exhibiting amphoteric character.

Process control devices utilizing fuzzy algorithms have been used for some time in chemical/biochemical engineering. Industrial and academic research chemists will now encounter in their laboratories both hardware programmed with fuzzy algorithms and software functioning via fuzzy rules.

Classification of input sensor data into small groups of overlapping data sets rather than into a larger number of non-overlapping sets is useful in programming real world controlling devices. Many scientists are unconvinced, however, by the success of fuzzy logic. They feel that it is simply a trendy shorthand redescribing of a fundamentally deeper principle and that it owes its practical success simply to the inadequacy of current measuring devices and the inadequacy of current computing devices. Given better algorithms and more computer power, surely, they think, control devices based on classical crisp logic will come into their own. The leader in the field Lotfi Zadeh (1981) has always insisted that, despite the similarity, there is a precise mathematical difference between the concepts of probability and possibility. He is supported by Ross (1995).

In conventional scientific theories or conventional control systems crisp data is fed into a system and processed via equations: algebraic, difference or differential. The advantage of this system for scientific research is the possibility that the mathematics may throw up some totally unexpected conclusions or actions: the model may predict the existence of black holes in the universe or that there is an ‘island of stability’ in the Periodic Table for elements of atomic number approximately 126. The disadvantage for controlling devices is that the imprecise nature of real data may amplify errors, and unexpected or erratic actions may result from the processing of the calculations. The first approach of fuzzy set theory was from the viewpoint of artificial intelligence, deriving inferences from vaguely formulated data. In the first generation (Linguistic Model, LM type) of fuzzy logic controllers, the input data is fuzzified by grouping it into manageable overlapping sets, then it is processed by inspection of a series of logical but linguistically framed rules of the type:

IF input sensor 1 is in range a AND rate input sensor 2 is in range b
THEN take predetermined action c
ELSE … Rather than mathematically operating on data input variables every time they are inputted, this controlling device merely ‘chooses’ which one of a set of predetermined pathways is indicated by analysis and subsequent fuzzy classification of the input variables. Obviously there is no scope for unexpected actions or discoveries: a scientist pursuing this methodology is seeking to justify his particular research program rather than disinterestedly seek after knowledge. Obviously, tinkering with the linguistic rules causes less unexpected ‘side effects’ than tinkering with mathematical equations when measured performance requires some modifications, leading to the conclusion that such systems are not only simpler but more robust in competitive situations.

Many real world LM controllers gave better results than classical logic controllers did 1975-1985. I will argue that the adoption of fuzzy principles by the Hughes-Ingold program 1933-1940 led to scientific advance at a time when the classical paradigm, based on classical reasoning, had stalled due to problems of the fuzziness of the data. However, second generation fuzzy logic controllers now exist (TSK or Takagi-Sugeno-Kang type; Yager & Filev 1994) in which the input data variables are classified into fuzzy sets but then the aforementioned ‘pathways’ subsequently chosen involve the use of classical mathematical equations i.e.

IF input sensor 1 is in range a AND input sensor 2 is in range b
AND input sensor 3 is in range c THEN feed the values a, b, c into a formula, process and take action d based on the result
ELSE … This type of reasoning is a hybrid between the original classical deterministic reasoning of conventional models and the fuzzy reasoning of the first generation LM type controllers. I suggest that the decline of the Hughes-Ingold program from 1956 onwards and its replacement by the Hammett-Roberts-Winstein program mirrors the transition from the original LM type controllers to the more sophisticated TSK type controllers in the real world technology of today. The simplicity and robustness of the Hughes-Ingold program eventually became counter productive.[1]

2. Fuzzy concepts in the Hughes-Ingold program

The Hughes-Ingold program of 1933-40 was designed to solve the problems arising in nucleophilic substitution from the adoption of a model of singularity of mechanism, i.e. adoption of a model envisaging bimolecular collisions leading to a single rate determining transition complex. They instead made the radical proposal of duality of mechanism:

	RX ¬¾® R⁺ + X^– then R⁺ + Z^-¾® RZ	(S_N1)
	Z^- + RX ¾® (Z…R…X)^- ¾® ZR + X^-	(S_N2)

It is not merely with the benefit of hindsight that we can recognize the crisp/fuzzy dichotomy compared with modern multi-faceted classification (see for example Jones 1984). A rival, crisper classification of organic nucleophilic substitution reactions was proposed in 1939 by Saul Winstein with a five mechanism classification one year before the Hughes-Ingold theory became the center of attention as a result of their powerful consecutive series of papers (Hughes & Ingold 1940; for further technical details of Hughes-Ingold model and Winstein’s model, see Akeroyd 2000).

In principle the transition state for a bimolecular collision can be reduced to a system of equations (see Lewis, McLaughlin & Douglas 1985 on the Marcus Equation, provided that steric effects are discounted), so the spread of products is determined intrinsically from the energy levels of the components of the transition state, a problem that can be solved mathematically by the researcher, provided s/he has correct data to input and access to powerful computers. In contrast, the predictions of the original Hughes-Ingold model followed a few simple rules analogous to the linguistic statements of a First Generation Fuzzy Controller:

IF the substrate is a primary aliphatic compound (R¹H₂CX)
THEN a unique transition state is formed with the incoming group ‘attacking from the back’ (classified as S_N2).
ELSE IF the substrate is a tertiary aliphatic compound (R¹R²R³CX)
THEN a free carbocation is formed first, adopting a planar conformation, followed by subsequent attack by the incoming group (classified as S_N1).
ELSE
IF the substrate is a secondary aliphatic compound (R¹R²HCX)
THEN both mechanisms run in parallel. ENDIF The Hughes-Ingold system rationalized a number of conceptual problems troubling chemists. One of these was that for primary aliphatic chlorides the hydroxide ion was a much more powerful reagent than a water molecule but for tertiary aliphatic chlorides the water molecule was more powerful. As observed by Bartlett and Knox (1939): "It seems out of all reason […] that the fundamental mechanism is the same."

When three different alkyl groups are substituted at carbon atom 1 of an alkyl halide the molecule exists in two distinct isomers which are not superimposable on each other, the d and l forms. These forms exhibit optical activity; i.e. they differently rotate the plane of polarized light. Secondary alkyl halides of the type R¹R²HCX also exhibit optical activity and on hydrolysis sometimes yield alcohols with complete inversion of configuration, (i.e. complete d > l or l > d conversion), sometimes partial racemization with inversion (incomplete conversion), sometimes full racemization (approximately 50:50 mixture of d and l).[2]

While traditional bimolecular transition state theory possessed a conceptual problem when explaining the frequent observation of full racemization, Hughes and Ingold had a conceptual problem when explaining the not infrequent phenomenon of partial racemization (Akeroyd 2000). This was ‘solved’ by the proposal that for a relatively unstable carbocation R⁺ with a short ‘lifetime’ before reaction with a water molecule, the departing halide ion would exert a ‘shielding effect’, hindering attack of solvent molecules from that direction.

From 1937 onwards, leading American physical organic chemists abandoned singularity of mechanism but continued opposition to the Hughes-Ingold scheme. In particular they mocked the concepts of ‘carbonium ion lifetime’ and ‘shielding effect’ of the leaving group as ‘vague’ and ‘difficult to quantify’ (Doering & Zeiss 1953, Gould 1959b, Swain et al. 1951, 1955a, 1955b). In our day, they could well have described them as fuzzy concepts containing linguistically imprecise terms.

They also might have objected philosophically that Hughes and Ingold were including extrinsic factors into the explanation of the mechanism of a chemical reaction: the movements of a particular ‘shielding ion’ will be totally arbitrary, determined by solvent effects and presumably obey statistical laws independent of the energy levels of the newly formed carbocation. They therefore pursued the logic of the transition state theory, while conceding the force of experimental results and some of the power of a visualizable model. In addition, they dismissed on energetical grounds the concept of a ‘free’ carbocation, and argued there must be effects from solvent molecules. Hughes and Ingold also agreed that the carbocations must be stabilized by solvent molecules, but they regarded this stabilization as a bulk aggregate effect, similar to the stabilization of alkali metal ions, and that there was no point in including ‘nearby’ solvent molecules in any stage of the mechanism.

Hammett and his PhD student Steigman (1937) proposed two types of polymolecularreaction mechanism for solvolyses:

RCl + nR’OH ¾® ROR’H⁺ + Cl(R’OH)_n-1^- (analogous to Hughes-Ingold S_N1) and RCl + nR’OH ¾® ROR’ + ROH_2⁺ + Cl(R’OH)_n-2^- (analogous to S_N2).

Two years later Winstein (1939) put forward his own theory, rejecting the concept of S_N1 ionizations and the ‘shielding effect’ as an explanation for racemization problems. He proposed a spectrum ranging from mechanism I (identical with Hughes-Ingold S_N2) for substitution by a negative ion, through a combined backside/frontside solvated transition state with the chlorine atom eventually being pulled off by the hydrogen bonding of a third alcoholic solvent molecule (II) and finally to a ‘frontside’ bimolecular transition state V which allowed retention of configuration.

We can admire the initial conception of the Winstein mechanistic spectrum. However, in this period there were none of the modern devices capable of detecting the presence of transient species, conformations of transition states, radioactive ‘label’ atoms. Physical organic chemistry relied on kinetic studies, studying the rate of the reaction under investigation and the spread of resulting products. Given the problems of fuzzy data and limited techniques, it is arguable that an appropriately constructed model to cope with the fuzzy data would be more effective than an over precise model, delivering only apparent precision while in fact amplifying errors.

I suggest that Hughes and Ingold accepted in principle the Fuzzy Rules 1, 2, 3, and 5 listed Ross (1995) when generating a heuristic for their ‘research program’. In paraphrased form they run:

IF state, input, and output variables are available for observation, measurement, and computation AND there exists a body of knowledge expressed in rules, common sense, intuition
AND a solution exists THEN we will design a model to the best of our available knowledge and within an acceptable range of precision.
ENDIF The fact that they persisted with their simple initial concepts post 1950 when the Americans started to achieve success with their more complex and more traditional models suggests that Hughes and Ingold did not initially set out with the fifth rule: that a simply ‘good enough’ heuristic for the time being is satisfactory. Their continued defense indicates that they felt that their heuristic was the optimum one. However, the published criticism of their American colleagues shows no doubt that they perceived it as a fuzzy heuristic, suitable only for ‘good enough’ results, but definitely too simple to serve as any thing more than a stepping stone towards the ‘optimum theory’.

3. Possibilistic Reasoning in the Hughes-Ingold Program

The molecularity of the rate determining step of a direct nucleophilic replacement reaction can be determined by the kinetics i.e. by measuring the rate of formation of one of the products or alternatively the rate of destruction of the substrate. Aliquots are drawn out at regular intervals and quickly titrated to estimate the concentration of the appropriate species. In a bimolecular reaction this rate of reaction would be proportional to the concentration of both species (‘second order kinetics’) whereas for a unimolecular reaction the rate should be proportional to the concentration of the substrate only and independent of the concentration of the nucleophile, when runs of varying concentration are made. Data is transformed mathematically so as to give the possibility of achieving a straight line graph of concentration against time.

This seems straightforward enough but one of the problems is that when the nucleophile is present in large excess the above second order relationship simplifies into that of the first order equation: the reaction is then said to exhibit ‘pseudo first order kinetics’.[3] This could be the case when tert-butyl bromide is hydrolyzed and also in many other reactions at the concentrations used by Hughes and Ingold 1933-1937.

However, after 1937, following a procedure initially published by the US physical organic chemists Hammett and Roberts (1937), they redescribed the kinetics for the mechanism for a S_N1 hydrolysis in the form

k_f k’

RX ¬¾
¾® R⁺ + X^- ¾® RY

k_r +Y^-
– X^-

with the rate

When (X^-) is vanishingly small (as at the beginning of a reaction) or when k_ris very small compared with k’ (R⁺ fairly unstable), this expression reduces to first order kinetics.

When, however, the concentration of X^- is not insignificant and k_r ~ k’ then deviations from first order kinetics might be expected (the ‘common-ion’ or ‘mass law’ effect). If the mechanism of hydrolysis was S_N2 via attack on RX by neutral water molecules then the reaction

RX + ^*X^-¾® R^*X + X^- would simply be an irrelevant side reaction.

If a reaction is following first order kinetics, or second order kinetics with the second reagent in large excess, the graph ln (A/A₀) against t is a straight line (Fig. 1; A is the current concentration of RX, A₀ is the original concentration of RX, t is the time).[4]

Figure 1: ln (A/A₀) against t. First order or pseudo-first order kinetics without ionic strength effect and mass law effect gives a straight line. Ionic strength effect increases and mass law effects decreases reaction velocity. These effects are predicted to be of different degree for S_N1 and S_N2 within probabilistic ranges. If the reaction is S_N1, developing amounts of X^- in the mixture could cause deviations to the right as time goes by (‘mass law effect’ > ‘ionic strength effect’) or deviations to the left (‘ionic strength effect’ > ‘mass law effect’). Also, the addition of extra amount of X^- at the start of a reaction should shift the whole curve to the right (‘common ion effect’) whereas the addition of a non-common ion, Z^-, should shift the whole curve to the left. This meant, paradoxically, that deviations from the expected straight lines of ln (A/A₀) plots, far from being inconclusive or evidence of faulty experimental technique, were in fact powerful evidence for a preliminary bond breaking step in the mechanism of the hydrolysis of tertiary aliphatic halides. As stated by Hughes and Ingold (1940, p. 961), they were able to make predictions for the series tert-butyl bromide to triphenylmethyl bromide and then start systematically looking for reactions in solvent mixtures which supported deviant behavior.

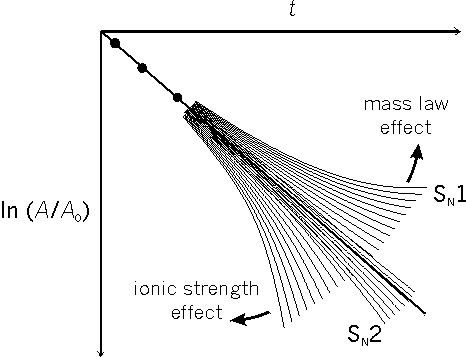
For a reaction obeying first order or pseudo-first order kinetics in the absence of both ionic strength effects and mass law effects it is possible to draw a straight line and make crisp predictions that the rest of the future plots will fall within a probabilistic boundary range. If ionic strength is steadily increased during the reaction, for example by formation of the ions H⁺and X^-, then it is possible to estimate (using Debye-Hückel Theory) the widening curved probable range.

However, although it is possible to devise a precise mass law equation to represent the mass law effect, there are too many rate constants included in it which may vary in different directions as the ionic strength changes in relation to the developing amounts of H⁺ and X^-. It is impossible to predict, on the basis of initial plots, the range within which future plotted points must fall for the experiment to be considered successful. The most that one can reasonably expect is that the points will fall consistently on at least one of a family of possible curves.

In the case of reactions following the S_N2 mechanistic pathway, there is a restriction on the number of possible curves (increasing ionic strength causing a small increase in the velocity of reaction), whereas if the mechanism is S_N1 there are a greater number of possible curves depending on whether the mass law effect is greater or lesser than the ionic strength effect. Any plot, drifting to the right in the resemblance of a curve, is fuzzy but important evidence for a preliminary bond breaking step in the mechanism. For a period of some twelve years, there was evidence for the simple and fuzzy Hughes-Ingold concept of all non S_N2 reactions operating via a ‘free’ carbocation R⁺with a conveniently ‘short’ or ‘reasonably short’ or ‘long’ ‘lifetime’. Before 1940, American physical organic chemists objected to the concept of an ionic mechanism in solvolytic reactions; from 1940 onwards, they objected to a fuzzy interpretation of an ionic hypothesis. While admitting the empirical kinetic evidence for a preliminary bond breaking step in the nucleophilic substitution reactions of the tertiary aliphatic compounds, they refused to accept the unmodified theory in its simple form.

Winstein started to work on the ‘Intimate Ion Pairs’ and ‘Solvent Separated Ion Pairs’ hypothesis for S_N1 reactions. This led to the American ‘modified Hughes-Ingold system’ overtaking the basic unaltered Hughes-Ingold system as continued by its progenitors.

4. Why did the fuzzy model succeed?

In this account I have put forward arguments that a research group which achieved tremendous influence on the development of physical organic chemistry (and also the way in which traditional organic chemistry is taught; cf. Jencks 1981) achieved their success by means of a mixture of fuzzy concepts and possibilistic reasoning. Because of the then lack of devices capable of detecting short lived reaction intermediates such as carbocations and the fuzzy nature of the data used in their theory generation (some of the results used went back to 1900 and obviously Hughes, Ingold and co-workers could not attempt to rework every experiment), they used a model based on a simple fuzzy concept (the ‘free’ carbocation in a S_N1 reaction) combined with possibilistic reasoning in the generation of the mass-law curves. One or two scientists have stuck their necks out and publicly admitted in their writings that they use possibilistic reasoning; to avoid any charges that my paraphrasing has introduced subtle distortions of meaning I quote their exact wording: In any real world situation our information about a system is too voluminous and intricate, and needs to be summarized; or it is approximate from the very beginning. A scientist, attempting to analyse such a system, implicitly asserts his belief that a number of significant things can be said about the system – if they can only be found! In his attempt to analyse a real world system, he is working with a model of it, simplified so as to be manageable and comprehensible. The danger of the assumption that this model can always be deterministic has been demonstrated by Gaines (1976).

In general, it can be said that unwarranted structural assumptions imposed on the working model can lead to dangerous artefacts that do not reflect anything that is contained in the real world data: this leads consequently to meaningless results […] we may still be able to provide answers to our questions such as: what structural relationships between the individual items analysed must exist? Which ones may exist? Which cannot exist? Which may exist perhaps if […]? These modal terms in which we all think, but which we usually rule out of our ‘scientific discourse’, are in fact the proper terms for possibilistic systems. [Bandler & Kohout 1981, pp. 219-220]

With regard to the aforementioned quote from Bandler and Kohout, Hughes and Ingold answered the following questions: Q. ‘What relationships in the analyzed data must exist?’

A. ‘One or more distinctive heterolytic pathway mechanisms sometimes operating in organic reactions.’

Q. ‘What relationships in the analyzed data may exist?’

A. ‘A simple mechanistic pathway involving the concept of ‘free’ carbocations.’

Q. ‘Which relationships in the analyzed data cannot exist?’

A. ‘The relationship that the mechanism of all organic reactions can be described by transition state theory (S_N2 mechanism).’

In addition, I would like to remark that the difficulties in making predictions from the initial plots of the mass law curves did not arise merely because of the practical difficulty of experimentally determining the constants k_r and k’, which might in principle in the future be calculable from thermodynamic data and powerful computers, but also from the indeterminacy of the system, as also mentioned by Bandler and Kohout. The mass-law equation is derived from first principles assuming the so called steady state principle, i.e. making the assumption that the concentration of R⁺ during the reaction is constant.

Now this is a pretty big assumption and, although we know that this concentration of R⁺ can neither steadily increase nor steadily decrease monotonically throughout the reaction,there is no reason why it should not fluctuate systematically between an upper bound and a lower bound in the course of the reaction. Such reactions have been observed and catalogued (‘oscillator’ reactions) where fluctuations are so gross as to lead to widely different product mixes depending on the time when the reaction is stopped. In the case of the Hughes-Ingold solvolytic curves, I am merely suggesting that fluctuations in the concentration of R⁺ lead to indeterminacy in the system: no two successive experimental runs will correspond with an ideal graph even in theory.

However, physical detection of carbocationic intermediates was beyond the technical apparatus of the time and similar support for the Hughes and Ingold program was bound not to be forthcoming. This example is the only one I am aware of where possibilistic reasoning was used to make leading scientists switch hypotheses, rather than simply concede that ‘such and such a theory has considerable merit’ or ‘such and such a theory is certainly making headway’.

One reason for the success of the early Linguistic Model Controllers based on Zadeh’slogic was their ability to incorporate the experience of inarticulate human operatives of the system in question into a machine programmable form. Earlier classical controllers based on equations were unable to do this as successfully. In a sense the simple fuzzy Hughes-Ingold model successfully incorporated the experience of previous generations of organic chemists, who, as is well-known, had been proceeding in a highly atheoretical manner from 1860-1930 (see for example Gould 1959c). One can therefore understand its success and also the reluctance of Hammett, Roberts, and Winstein to abandon the mathematics entirely in their model and therefore to try and build up a hybrid system containing the best of the old and the best of the new: i.e. a system resembling the Takagi-Sugeno-Kang (TSK) controllers using both fuzzy principles and classical equations.

Notes

[1] Winstein’s (1956) Dual Ion Pair hypothesis is still accepted today (see Lund 1995). It was immediately criticized as being fuzzy by Hughes and Ingold (1957) in a paper received by the Journal of the Chemical Society on Oct. 5, 1956, and Jones (1984), in an undergraduate text, comments "because it is so flexible it leaves room for doubts about the precise mechanisms of reactions that fall between clear-cut extremes." Unlike the Hughes and Ingold model, the Winstein model received experimental corroboration almost immediately via the tool of isotopically labelled oxygen atoms (Denney 1957).
The analogy with the TSK controllers can be seen by inspecting the equations given on p. 329 of Winstein (1956), which can be reformulated using the IF … THEN rules of TSK, i.e
IF k_s^III>> k_-2
THEN equation (6) degenerates to k_t = k₁[ 1 + k₁/k₂]
ELSE …
[2] Hydrolysis with retention of configuration is possible if one of the R groups contains another substituted heteroatom Y. In this account, we are discussing normal C_nH_2n+1type R groups.
[3] Other problems arise if the total concentration of the nucleophile is made up of associated ion pairs and ‘free’ ions e.g. Na⁺OH^-« Na⁺ + OH^-.
At higher concentrations, estimating the amount of total base remaining will not reflect the concentration of the active species OH^- that is responsible for affecting the rate of the reaction. Departures from second order kinetics are expected which may approximate to first order kinetics.
[4] For convenience Hughes & Ingold often worked with the expression k₁ = (2.3/t) log₁₀(A₀/A) rather than the ‘classical’ plots used here (see Journal of the Chemical Society, (1933), p. 1573).

References

Akeroyd, F.M.: 2000, ‘The rise of the Hughes & Ingold Theory from 1930-42’, Foundations of Chemistry, 2, 99-125.
Bandler, W.; Kohout., L.J.: 1981, ‘Semantics of implication operators and fuzzy relational products’, in: E.H. Mamdani & B. R. Gaines (eds.), Fuzzy Reasoning and its Applications, Academic Press, London, pp. 219-46.
Bartlett, P.D.; Knox, L.H.: 1939, ‘Bicyclic Structures Prohibiting the Walden Inversion’, Journal of the American Chemical Society, 51, 3184-92.
Chang, R.: 1998, Chemistry, 6^th edn., Mc Graw-Hill, New York, pp. 317, 628.
Denney, D.B.; Goldstein, B.: 1957, ‘An Oxygen-18 Tracer Study of the Rearrangement in 2-Pheny-1-Propyl Bromobenzenesulphonate’, Journal of the American Chemical Society, 79, 4948-51.
Doering, W.; Zeiss, H.H.: 1953, ‘Methanolysis of Optically Active Hydrogen 2,4 dimethylhexyl-4-pthalate’, Journal of the American Chemical Society, 75, 4733.
Gaines, B.R.: 1976, ‘Foundations of Fuzzy Reasoning’, International Journal of Man-Machine Studies, 6, 623-68.
Gould, E.S.: 1959a-c, Mechanism and Structure in Organic Chemistry, Holt, Rinehardt and Winston, New York, (a) pp. 299-302, (b) p. 269, (c) p. 2.
Hammett, L.P.; Roberts, I.: 1937, ‘The Mechanism of Substitution Reactions: Benzyl Chloride with Mercuric Salts’, Journal of the American Chemical Society, 59, 1063-8.
Hughes, E.D.; Ingold, C.K.: 1940, ‘Mechanism of substitution at a Saturated Carbon Atom. Parts XI-XXIII, Journal of the Chemical Society, 913-1024.
Hughes, E.D.; Ingold, C.K.; Mok, S.F.; Patai, S.; Pocker, Y.: 1957, ‘Mechanism of substitution at a Saturated Carbon Atom. LVIII.’, Journal of the Chemical Society, 1265-70.
Jencks, W.P.: 1981, ‘How does a Reaction choose its Mechanism?’, Chemical Society Reviews, 10, 345-65.
Jones, R.A.Y.: 1984, Physical and Mechanistic Organic Chemistry, 2^nd edn., Cambridge University Press, Cambridge, pp. 149-150.
Lewis, E.S.; McLaughlin, M.L.; Douglas, T.A.: 1985, ‘Methyl tranfers. 10. The Marcus Equation. Application to Soft Nucleophiles’, Journal of the American Chemical Society, 107, 6668-73.
lund, H.; Daasbjerg, K.; Lund, T.; Pedersen, S.U.: 1995, ‘On Electron Transfer in Aliphatic Nucleophilic Substitution’, Accounts of Chemical Research, 28, 313-9.
Ross, T.J.: 1995, Fuzzy Logic with Engineering Applications, McGraw-Hill, New York, pp. 474-5.
Steigman, J.; Hammett, L.P.: 1937, ‘Solvolytic Reactions of alpha-Phenylethyl Chloride’, Journal of the American Chemical Society, 59, 2536-42.
Swain, C.G.; Langsdorf, W.P.: 1951, ‘Concerted Displacement Reactions. VI’, Journal of the American Chemical Society, 73, 2813-9.
Swain, C.G.; Kreevoy, M.M.: 1955a, ‘Mechanism of Anion Exchange in Trityl Chloride in Benzene’, Journal of the American Chemical Society, 77, 1122-8.
Swain, C.G.; Moseley, R.B.: 1955b, ‘Rates of Solvolysis of Tri phenyl Methyl Fluoride’, Journal of the American Chemical Society, 77, 3727-31.
Winstein, S.: 1939, ‘the Solvolysis of t-butyl chloride’, Journal of the American Chemical Society, 61, 1635-9.
Winstein, S.: 1942, ‘The Role of Neighbouring Groups in Replacement Reactions. I-V’, Journal of the American Chemical Society, 64, 2780-1 (2780).
Winstein, S.: 1956, ‘Salt Effects and Ion Pairs in Solvolysis and Related Reactions’, Journal of the American Chemical Society, 78, 328-35.
Yager, R.R.; Filev, D.: Fuzzy Modelling and Control, J. Wiley, New York, 1994, pp. 192-4.
Zadeh, L.A.: 1981, ‘PRUF – a meaning representation language for natural languages’, in: E.H. Mamdani & B.R. Gaines (eds.), Fuzzy Reasoning and its Applications, Academic Press, London, pp. 1-66.

F. Michael Akeroyd:
Bradford College, BD7 1AY, U.K.; m.akeroyd@bilk.ac.uk

Copyright Ó 2000 by HYLE and F. Michael Akeroyd