Computational Models and Virtual Reality

1. Molecular Models and Graph Theory

The well-known models of molecules with different information for a chemist are derived from the molecular structure hypothesis: a) The 3-dimensional ball-and-stick model with balls for the atomic nuclei, sticks for the atomic bonds and their angles, b) its 2-dimensional representation as structural formula, and c) its 1-dimensional representation as linguistic name which can be derived from the structural formula. Graphic models are applications of mathematical graph theory which is a part of combinatorial topology. This mathematical theory became fundamental to chemistry, when in the midst of the last century the molecular structures of chemical substances were discovered (Mainzer 1997b).

Van’t Hoff’s stereochemistry regarding the three-dimensional structure of molecules must initially have appeared to be a highly speculative idea with a certain proximity to platonic forms. Kekulé may have been particularly adept at three-dimensional visualization as a result of his prior study of architecture. Simultaneously with stereochemistry, geometry and algebra were also undergoing fruitful development. Van’t Hoff’s success in experimental explanation and prediction made his geometry and algebra of the molecule soon a method accepted by chemists. However, it lacked any definitive physical justification. At this stage of development, stereochemistry remains a successful heuristic approach which meets chemists’ need for a means by which they can visualize their structural analyses.

From an experimental point of view, the shape of molecules can be illustrated by an outer envelope of their electronic charge distributions. These representations are similar to the pictures of atoms which we can obtain today experimentally by the scattering of electrons in super microscopes or from the scanning tunneling electron microscope. It is the distribution of charge that scatters the X-rays or electrons in these experiments. Thus, it is the distribution of charge that determines the form of molecular matter in the 3-dimensional space.

Mathematical methods of differential topology enable us to identify atoms in terms of the morphology of the charge distribution. The charge density D(r) is a scalar field over 3-dimensional space with a definite value at each point. Positions of extrema in the charge density with maxima, minima, or saddles, where the first derivative of D(r) vanish, can be studied in the associated gradient vector field Ñ D(r). Whether an extremum is a maximum or a minimum is determined by the sign of the second derivative or curvature at this point. The gradient vector field makes visible the molecular graph with a set of lines linking certain pairs of nuclei in the charge distribution.

Local maxima in an electronic charge distribution are found only at the positions of the nuclei. This is an observation based on experimental results obtained from X-ray diffraction and on theoretical calculations on a large number of molecular systems. Thus, a nucleus seems to have the special role of an attractor in the gradient vector field of the charge density. In short: The topology of the measurable charge density defines the corresponding molecular structure.

The molecular graph is the network of bond paths linking pairs of neighboring nuclear attractors. An atom, free or bound, is defined as the union of an attractor and its basin. Atoms, bonds, and structure are topological consequences of a measurable molecular charge distribution. In a next step, it is necessary to demonstrate that the topological atom and its properties have a basis in quantum mechanics. Topological atoms and bonds have a meaning in the real 3-dimensional space. However, this structure is not reflected in the properties of the abstract infinite-dimensional Hilbert-space of the molecular state function. The state function contains all the information that can be known about a quantum system of nuclei and electrons. From an operational point of view, there is too much and redundant information in the state function because of the instinguishableness of the electrons and because of the symmetry of their interactions. Some of that is unnecessary as a result of the two-body nature of the Coulomb interaction. Thus, there is a reduction of information in passing from the state function in the infinite-dimensional Hilbert space to the charge distribution function in the real 3-dimensional space. On the other hand, we thus get a description of the molecular structure in the observable and measurable space.

Quantum chemistry uses several mathematical procedures of approximation to achieve this kind of reduction. A well-known approximation is the Born-Oppenheimer procedure that allows a distinction of the electronic and nuclear mass of a molecule. We get the nuclear structure of a molecule that is represented by its structural formula. In order to distinguish the electrons as quasi-classical objects in orbitals, the Hartree-Fock method is sometimes an appropriate approximation for the electronic state function. The coincidence of the topological and quantum definitions of an atom in a molecular structure means that the topological atom is an open quantum subsystem of the molecular quantum system, free to exchange charge and momentum with its environment across boundaries which are defined in the three-dimensional real space.
 
 
 

2. Computational Models and Visualization

Topological forms can be characterized by topological index numbers correlated to certain chemical properties (e.g. boiling point, toxicity; cf. Bonchev 1983). Examples are hydrocarbon molecules with nearly the same volume but different topological structures and properties. An example of a topological index is the Wiener index. If the molecular structure is represented in a topological graph with atoms as nodes and bonds as edges, the Wiener index is the sum of all shortest connections between the atoms along the edges by counting the number of edges. The Wiener index correlates the molecular structure with many properties of certain chemical substances, e.g., boiling point, viscosity, and refractive index.

The bonding index refers to the topological structure of a molecule by ranking the atomic modes and their connection edges. The rank of an edge is the product of the ranks of its two modes. The bonding index of a molecule is the sum of the ranks of all molecular edges. The bonding index can be computed for molecular fragments (e.g. path, cluster, or closed ring). They can be correlated to chemical properties of certain medicaments, the toxicity, smell, or taste of new substances.

The number of double bond equivalents corresponds to the number of independent rings and double bonds in a molecule. A special topological index results if it is multiplied with the relative frequency of open chains and closed rings. That index can be correlated to the amount of soot produced by burning hydrocarbon. Polycyclic aromatic hydrocarbon compounds contain certain topological regions which are involved in chemical reactions with cancerous effects. They can be characterized by topological indices, too.

A challenge to modern chemistry is the development of computer-aided molecular design and artificial intelligence (Brandt & Ugi 1989, Mainzer 1992). In the 60s, the application of knowledge based expert systems started with the DENDRAL program in chemistry. It automatically searches chemical structural formulas according to a given molecular formula and the corresponding mass spectrogram. In this case, the research strategy of a chemist tries to generate topologically possible molecular structures and to test or select the chemically possible ones. Mathematically, the research strategy is performed by a recursive algorithm (‘British Museum algorithm’) in a LISP-program (Mainzer 1995).

In the 80s, there was a boom of programs producing molecular models by CAMD (computer aided molecular design) methods. A simpleexample is a program using a method to draw 2D structures of organic molecules, including ring systems and stereoisomers, which can automatically be converted into 3D models. The automatic process uses an advanced distance geometry algorithm. Another program generates and displays molecular volumes for one or more molecules, and makes a range of comparisons between the volumes. It can also generate volumes from the output of a dynamic calculation and from a systematic search file.

The complex shape of macromolecules dramatically effects the electrostatic field and can be crucial to their functions. The program calculates these electrostatic properties and visualizes complex structures. As a result, the researcher can predict the electrostatic effects and screen compounds before experimentation. The program uses a finite difference algorithm to solve the Poisson-Boltzmann-equation. There are also CAMD-programs for simulating the molecular dynamics by trajectories in 3D-models. These programs incorporate a broad spectrum of molecular mechanics and dynamics methodologies. By using an empirical force field as foundation, minimum energy confirmations as well as families of structures and dynamic trajectories of molecular systems can be computed. The program can help develop and refine working hypotheses as well as guide experimental directions.

In general, complex CAMD-programs consist of several modules combining more and more activities of a researcher. There are the following standard modules: Viewer, for viewing and comparing molecules, contours, and other graphic objects; Builder, for constructing new molecules from molecular fragments or atoms; Docking, for calculating the interaction between two molecules using an combination of van der Waals energy and/or Coulomb energy. Optional modules of specific interest are, e.g., Biopolymer, for building and modifying proteins, peptides, and nucleic acids; Analysis, for analyzing trajectory data, conformational data etc. The program should enable chemists to design drugs, chemicals, and materials. The goal is to help scientists comprehend the amount of information produced by theory-based models, and to focus the research in a more productive manner.
 
 

3. Virtual Reality in Chemo- and Bioinformatics

The World Wide Web started with the 2D format of HTML (hypertext markup language). But the interactive 3D world of VRML is the future of the web. The speed of realization only depends on various technical aspects like bandwidth and CPU requirements. The VRML 1.0 specification of 1995 was a means of creating static 3D worlds. The extension of VRML 2.0 provides enhanced 3D worlds, interaction, animation, and prototyping. Complex molecular structures, which had no chance of visualization before, can now be interactively experienced and designed. Further on, the Internet programming system Java is a flexible environment for the integration of VRML into chemical teleworking. Collaborative work on 3D molecular structures can be realized by research groups spread over the World Wide Web.

Object-oriented programming of VRML corresponds to the structure of complex molecules consisting of atomic building blocks and their bonds. From a methodological point of view, object-oriented programming relies on basic ideas of mathematical systems theory. According to the complex systems approach, any system can be separated from the external environment by some real or fictitious system boundary. The features of the system boundary determine the exchange of material, energy, and information between the system and its environment, corresponding to the input and output transfer in information systems. Further on, any system is defined as a structure of related subsystems. Stepwise decomposition of the system leads to smaller subsystems on different hierarchical levels of details until the level of elementary subsystems, which are regarded as not being further decomposable. An elementary subsystem can be an abstract or a real material entity.

These modeling entities support the development and the handling of mathematical models. Composite modeling objects at a higher degree of complexity are derived by selection and aggregation of the predefined elementary modeling objects. In object-oriented programming, an object refers to a data structure that is used to mimic the conceptual entities of the application area to be modeled. Different types of modeling objects can be represented by object classes. A molecular structure with atomic elements and bonds corresponds to a data structure with inheritance relationships between classes and their subclasses. ‘Inheritance’ means that manipulations of object classes (e.g., turning a molecular structure) are transmitted to their subclasses (e.g., the atoms of a molecule). The similarities among the modeling objects can be utilized to develop class taxonomies of modeling objects.

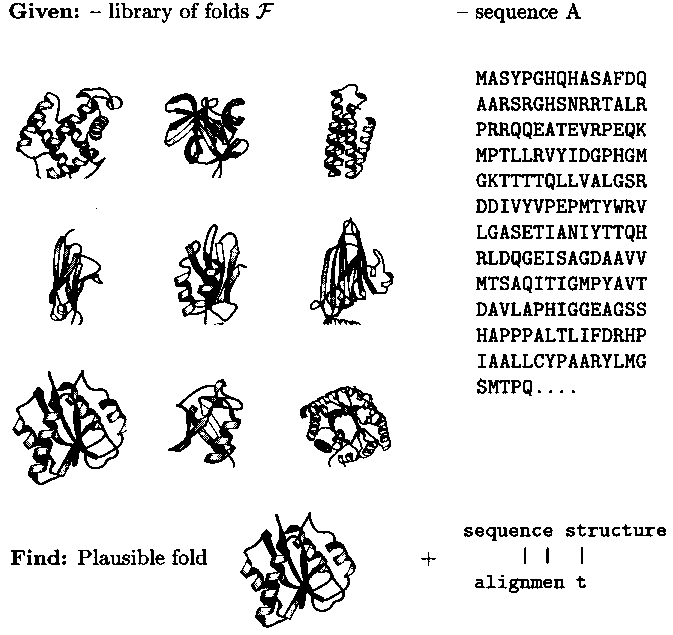
Object-oriented modeling of molecular structures provides new tools of computer-assisted problem solving in chemistry. An example is protein fold recognition in biochemistry (Fig. 1): Given a virtual library of folds representative of the database of experimentally solved structures and a query sequence, the tool identifies that fold among the representatives which is most plausible, i.e. most similar to the predicted structure, for the sequence in question. This is done by computing sequence-structure alignments of the query sequence with each of the representatives and then ranking the latter according to the alignment score as an approximation of sequence-structure computability. The alignments with the top-ranked structures define detailed mappings of sequence to structure positions which immediately lead to rough structure models for the query sequence.

The exhaustive comparison results in a relation of sequence similarities within the genome. The visualization of such a relation is the genome sequence similarity graph. A graph is a network of vertices connected by edges. Each vertex of the graph represents a DNA block. An edge connecting two vertices represents a similarity relationship between two blocks. Each vertex contains information about its position on a distinct chromosome. Edges are labeled according to their similarity score values. Each vertex contains associated information about known genetic elements identified by other sequence analysis methods. In the framework of the object-oriented programming language Java, the Genomebrowser and the visualization of the genome sequence similarity graphs support powerful services of interactive biochemical research.
 
 

4. Perspectives of Chemical Research in the Age of Computer Networks

Chemistry does not only explore static structures, but also dynamic processes like chemical reactions as applications of kinetic equations. They correspond to the ‘dynamical view’ of applied mathematics. The prediction or determination of chemical events and properties need sophisticated computational procedures of numerical mathematics, approximation, and algorithmic theory. Typical examples are ab initio computations in quantum chemistry. These applications correspond to, what I call, the ‘numerical view’ of applied mathematics. Today, the numerical procedures become more and more efficient by the increasing capacities of computer technology, for example, the power of massively parallel computers.

However, chemistry is not only interested in numerical procedures, but also in the construction of 3D geometric models and the derivation of linguistic terms such as chemical formulas. In the past, these activities have been already assisted and even simulated by knowledge based expert systems, 3D computer aided molecular design (CAMD) programs, and computer aided knowledge processing of AI-programs. This aspect of modern computer mathematics is called the ‘program view’, which I have demanded for modern philosophy of science (Mainzer 1995, p. 705). With the development of object-oriented programming languages, virtual chemical structures can be designed and explored in computer networks by worldwide distributed research groups.

There is a clear tendency of research in all natural sciences that the traditional experiment in the laboratory is assisted by computer experiments. They are not only supplementary visualization. An example is the dendritic growth of materials. For this kind of diffusion limit aggregation (DLA), there is no analytical theory, but a direct computer simulation. Diffusion processes are mathematically considered as random walks of particles. The growth of DLA-clusters is simulated by an algorithm that can easily be translated into an appropriate programming language (Mainzer 1999, p. 114). Algorithms and programs of DLA-processes can be tremendously accelerated by high-speed computers. Thus, the fractal dimensions of even large dendritic clusters are computable. Typical structures of dendritic growth can be observed and classified under varying conditions of complex experiments, providing fruitful hints on lab experiments and industrial design of new materials. For example, consider the chemistry of polymerization. Long chains of identical monomers play an enormous role in technical applications of materials science, but also in living organisms with complex DNA structures. Mathematically, the growth of polymeric chains seems to be simulated by random walks, again. However, random walks may cross themselves, polymeric chains may not. Thus, polymeric chains are examples of self-avoiding-walk (SAW)-processes. There are no differential equations for their computation. In general, there is only the possibility of direct computer experiments or lab experiments.

However, experiments in chemical laboratories spend time, materials, and money. In the age of accelerating innovation cycles and increasing costs in technology and industry, computer experiments will help to select and decide on future tendencies of research. Their programs provide strategies to refine scientific conceptions and to focus the research in a productive manner. They help to prevent and to select less productive, expensive or even dangerous experiments in the laboratory. But, of course, research cannot do without lab experiments. Finally, computer networks enable worldwide collaboration of chemists on virtual objects of research. From an epistemic point of view, computational models and virtual reality are an essential enlargement of human imagination and recognition, opening new avenues of research. However, virtual reality in chemistry does not compete with the wet reality of chemical substances in nature. It is a software tool of modeling, no more and no less.
 
 

References: