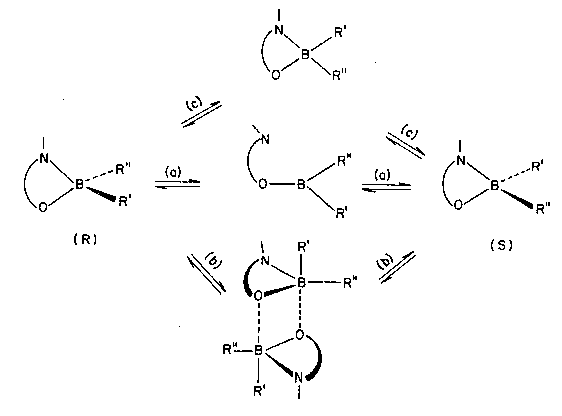
Figure 1. Three reaction mechanisms for inversion of stereochemical
configuration at a tetrahedral boron center.
HYLE--International Journal for Philosophy of Chemistry, Vol. 3 (1997), pp. 3-28:
Abstract: We begin by presenting William of Ockham's various formulations
of his principle of parsimony, Ockham's Razor. We then define a reaction
mechanism and tell a personal story of how Ockham's Razor entered the study
of one such mechanism. A small history of methodologies related to Ockham's
Razor, least action and least motion, follows. This is all done in the
context of the chemical (and scientific) community's almost unthinking
acceptance of the principle as heuristically valuable. Which is not
matched, to put it mildly, by current philosophical attitudes toward
Ockham's Razor. What ensues is a dialogue, pro and con. We first present
a context for questioning, within chemistry, the fundamental assumption
that underlies Ockham's Razor, namely that the world is simple. Then we
argue that in more than one pragmatic way the Razor proves useful, without
at all assuming a simple world. Ockham's Razor is an instruction in an
operating manual, not a world view. Continuing the argument, we look at
the multiplicity and continuity of concerted reaction mechanisms, and at
principal component and Bayesian analysis (two ways in which Ockham's Razor
is embedded into modern statistics). The dangers to the chemical imagination
from a rigid adherence to an Ockham's Razor perspective, and the benefits
of the use of this venerable and practical principle are given, we hope,
their due.
Keywords: Ockham's Razor, reaction mechanism, principle of least action, principle of least motion, principal component analysis, Bayesian analysis.
Scientists think they are born with logic; God forbid they should study this discipline with a history of more than two and a half millenia. Isn't it curious that some of our competitors and critics, pretty good scientists (except when they review our papers), seem to be strangely deficient in logic!
While scientists think they can do without philosophy, occasionally principles of logic or philosophy do enter scientific discourse explicitly. One of these philosophic notions is Ockham's Razor, generally taken to mean that one should not complicate explanations when simple ones will suffice. The context in which Ockham's Razor is used in science is either that of argumentation (trying to distinguish between the quality of hypotheses) or of rhetoric (deprecating the argument of someone else). Either way, we think that today appeal to the venerable Razor has a bit of a feeling of showing off, of erudition adduced for the rhetorical purposes. This attitude reveals a double ambiguity. The first is toward learning - today's science, no longer elitist, does not depend on men steeped in classical learning. And appeal to Ockham's Razor also points to a certain ambiguity in the relationship of science to philosophy.
We thought it would be interesting to learn something of the principle and its various meanings. We also present a personal discussion on the use of Ockham's Razor in chemistry, with specific reference to the analysis of reaction mechanisms.
To his peers and to the world of theology William of Ockham (ca. 1286 - 1347) was and is a leading 'scholastic' Philosopher.[1] This is the late period of the Middle Ages; the wisdom of the Greeks is reintroduced into Europe through Al Andalus, Islamic Spain. It is a time of great minds in the religions; the time of the Rabbis Moses ben Maimon (Maimonides) in Cordova and Egypt, Moses ben Nachman (Nachmanides) in Gerona, Shlomo Yitzhaki (Rashi) in Troyes. It is the time, or shortly after the time, of St. Thomas Aquinas, of Roger Bacon, of Duns Scotus. The philosophy of Aristotle, with its far-reaching rationality, finds a resonance in the agile minds of Catholic theologians. The glory of God merges in their work with the path of reason.
William of Ockham (or Occam) was not only a theologian, but a great logician. A case has been made for his awareness of many of the principles of mathematical logic that were not mathematicized until 600 years later.[2] One of the tools he used routinely in his reasoning is what is known in philosophy as the principle of parsimony, and popularly as Ockham's Razor.
Just as for the Golden Rule, there are many ways of stating Ockham's Razor. Here are four that William of Ockham used in his works:[3]
(A) It is futile to do with more what can be done with fewer. [Frustra fit per plura quod potest fieri per pauciora.]
(B) When a proposition comes out true for things, if two things suffice for its truth, it is superfluous to assume a third. [Quando propositio verificatur pro rebus, si duae res sufficiunt ad eius veritatem, superfluum est ponere tertiam.]
(C) Plurality should not be assumed without necessity. [Pluralitas non est ponenda sine necessitate.]
(D) No plurality should be assumed unless it can be proved (a) by reason, or (b) by experience, or (c) by some infallible authority. [Nulla pluralitas est ponenda nisi per rationem vel experientiam vel auctoritatem illius, qui non potest falli nec errare, potest convinci.]
Philosophers and historians are generally puzzled as to why the principle of parsimony should be called Ockham's Razor. The principle is not original to William of Ockham. Versions of it are to be found in Aristotle, and nearly verbatim variants occur in the work of most scholastic philosophers.[4] Though Ockham used it repeatedly and judiciously, "he clearly does not regard it as his principal weapon in the fight against ontological proliferation"[5].
We suspect that the association is due to the strength of the razor metaphor rather than anything else. Scholastic and theological arguments were complex; to cut through them, to reach the remaining core of truth quickly, was desperately desirable. Whoever rechristened the principle of parsimony as Ockham's Razor (the earliest reference appears to be to Etienne Bonnot de Condillac in 1746)[6] was creating an easily imagined image. Metaphor reaches right into the soul.
The last, most extensive formulation of Ockham's Razor, (D) above, is intriguing. Note the 'religious exclusion' in it. It refers to the Bible, the Saints and certain pronouncements of the Church. This testimony to the faith of William did not stop him from questioning the reasoning of Pope John XXII, when the Pope's writings came in conflict with earlier church authority. In the context of science, especially interesting is part (b) of version D of the Razor, that experience (experientia) can serve to justify plurality. There is no reason not to think of 'experience' here as 'experiment', even though the idea of a scientific experiment lies centuries in the future. William of Ockham's method (and that of Aristotle) empowers the human senses as arbiters. His method accepts what we now call science.[7]
Six and a half centuries is a lot of time; it is also very little time. In the Middle Ages one had protochemistries - fermentation, metallurgy, ceramics, alchemy, dyeing. People have always transformed matter in ingenious ways. The Renaissance came, then the Industrial and Scientific Revolutions. Now there is chemistry, a true science, an industrial empire, a profession. Beautiful molecules are made, fifteen million of them unknown to Nature. People ask questions "How does this reaction run?" "What is the mechanism (a very Newtonian clock-work type of question) of that reaction?" And remarkably, six hundred and fifty years after he died, they invoke William of Ockham's restatement of the principle of parsimony, that old Ockham's Razor, to help them reason out what happens.
Let us first define what is to be meant by the term 'reaction mechanism'. The notion of the mechanism of a chemical reaction consists of a description of all 'elementary' steps in the transformation of reactants into products. On the molecular level the mechanism includes, in principle, knowledge of the geometry and relative energy of all structures involved, including isolable or potentially isolable intermediates and transition states, the latter representing the turning points along the minimal energy paths connecting all interconverting species. Following another line of thinking, the reaction mechanism traces the evolution of a chemical system along the reaction trajectory, i.e., the line linking reactant and product molecules in the space of all nuclear coordinates. The concept of a potential energy surface (PES), with all its attendant limitations, is essential to this definition.
Given the definition of a reaction mechanism, the drawing of an analogy with the mechanical description of moving particles is obvious. A predictable consequence was the early application of the principles and methods developed so successfully in classical mechanics to the treatment of mechanisms of chemical reactions. Before the idea of a molecule ever took hold, there had been developed the principle of minimal action, first introduced by Pierre Louis Morveau de Maupertuis and universally applied by Leonhard Euler in ballistics, central force motion, etc. According to this principle, spontaneous movements are always associated with minimal changes in the quantity of 'action', the latter a well-defined physical variable. Reporting in 1744 to the Académie des Sciences of Paris on the principle of minimal action, de Maupertuis stressed, in particular, that light chooses neither the shortest line, nor does it follow the fastest path. Instead, light takes the path which gives real economy (cf. the law of parsimony), i.e., where the quanitity of action is minimal.[8] Minimal action is itself a beautiful, economic way to get at the heart of physical motion. And it found a place in the new quantum mechanics, most elegantly in the work of de Broglie, Schwinger, and Feynman.[9]
It is thus hardly surprising that when in the 1930's studies of mechanisms of chemical reactions had grown in importance, indeed to become the intellectual focus of the rapidly developing area of physical organic chemistry, the key generalizations relevant to reaction mechanisms were made in the spirit and in the terminology of mechanics. Perhaps, the first step in this direction has been taken even earlier, when A. Muller in 1886, i.e., at a time when molecular theory was still young, introduced the rule of least molecular deformation in the course of chemical transformation.[10] The idea was appealing, and found its place in a number of textbooks as the principle of minimal structural change.[11] In its most general terms it was formulated by F. Rice and E. Teller, who in 1938 proposed the principle of least motion (PLM) according to which "Those elementary reactions will be favored that involve the least change in atomic position and electronic configuration"[12]. In the context of the orbital symmetry rules that were to come into organic chemistry 27 years later, the inclusion of electronic configurations in the Rice and Teller formulation is noteworthy.
To apply the PLM to a certain reaction, the constituent atoms of the molecules of reactant and product must be displaced with respect to one another so that their nuclear motions (usually measured by their squares) are minimized. Indeed, a good number of organic reactions of the rearrangement, decomposition, and elimination type have been shown to follow those reaction pathways that do obey the requirements of the PLM. The extreme simplicity of the relevant computational technique and, more importantly, the clarity of the underlying idea, assured broad application of the PLM treatment of reaction mechanisms, particulary where a choice between several conceivable pathways was needed.[13]
It was always perfectly well understood that PLM represents a very, very simplified theoretical model of the actual motion of nuclei and electrons in the course of chemical reaction. That motion is properly described by the equations of quantum mechanics. None doubted that quantization of electronic, vibrational and rotational states mattered. And that one has to take a dynamic view, describing the real reaction by the totality of the myriad trajectories followed by an ensemble of real molecules in phase space. Still, PLM met a desire for simplicity. Given that it was simplistic, deviations from, or even incompatibility with, the PLM predictions, met in a number of applications of the principle, were never regarded, we think, as final indictments of a mechanistic hypothesis.
In contrast to this forgiving attitude toward deviations of a simple theory, the chemical community turns out to be not so tolerant when important, accepted ideas seem to be threatened. Let us give an example, drawing on personal experience.
In 1982 one of the authors (VIM) published a preliminary account of the experimental observation of inversion of stereochemical configuration at a tetrahedral boron center.[14] Several possible reaction pathways that might, in principle, connect the interconverting stereoisomers were enumerated. These included (Fig. 1): (a) intramolecular (dissociative) and (b) intermolecular (associative) routes, both involving bond-breaking processes at the tetrahedral boron, as well as (c) intramolecular inversion occurring through an intermediate tetracoordinate planar boron species, in which all four bonds to boron are retained (although their strength changes drastically).

Figure 1. Three reaction mechanisms for inversion of stereochemical
configuration at a tetrahedral boron center.
Whereas the intermolecular variant of the bondbreaking mechanism was ruled out on the strength of the experimental evidence then available, no unequivocal choice could be made at the time between the two remaining possibilities, (a) and (c).
The Rostov-on-Don authors could not abstain from the temptation of giving preference to the more exciting non-bond-breaking alternative mechanism (c). This choice turned out to be an error, as detailed experimental study later revealed.[15] But even before convincing evidence in favor of a bond-breaking mechanism was presented, the uncommon interpretation of the 'square-planar boron' mechanism of inversion elicited a quick response. Researchers from the University of East Anglia [16] pointed to the fact that the rate of the inversion process was comparable to that of bond-breaking processes in compounds structurally similar to those studied by the Rostov-on-Don group. On this basis they concluded that the inversion reaction follows the dissociative bond-breaking route, a mechanism with a venerable history going all the way back to the classic 1912 work by Alfred Werner on stereoisomerization of cobalt complexes.
While this was indeed a weighty argument in favor of the bond-breaking pathway, the reasoning of the English researchers was by and of itself not yet conclusive. Perhaps this was why they in turn were seduced by a crumb of philosophy, supporting their argument by the statement that following the dissociative pathway, in preference to the bond-conserving inversion "is also a natural result of the application of Occam's chemical razor principle: mechanisms should not needlessly be multiplied."
East Anglia and Rostov-on-Don are hardly enemies; the chemistry got sorted out in the end. Nevertheless, it is interesting to reflect on why appeal to such a general modality of reasoning as Ockham's Razor seemed to be quite appropriate in tackling such a specific problem as the mechanism of a certain chemical reaction. The answer is to be found, we think, in the nature of the theoretical construction which the reaction mechanism represents.
In general, the mechanism of a reaction can neither be directly observed, nor can it be deduced with absolute certainty on purely experimental grounds. It would be nice if the world were that simple. But it isn't. We are not convinced either that femtosecond spectroscopy, an incredibly fast and beautiful way of observing nature, will give the requisite mechanistic answers. The mechanism of a reaction is a logical construction based on a perforce limited set of experimental facts, which are then interpreted by human beings in the framework of current, fashionable and ephemeral theoretical models. And it is logic, with its laws and rules, that makes it possible to arrange observations in harmony with relevant concepts and hypotheses. Ockham's Razor belongs to the category of logical rules which indicate how to process experimental facts. It shows the way to the best fit of observables to the least complicated possible interpretation. It is, therefore, by no means accidental that in many textbooks concerned with the problem of reaction mechanisms, from introductory to advanced ones,[17] [18] Ockham's Razor is mentioned among the significant criteria to be met when determining a mechanism.
The utility of Ockham's Razor in the selection and classification of reaction mechanisms has proven itself in chemistry, just as it has in various other areas of natural science.[19] Ockham's Razor must indubitably be counted among the tried and useful principles of thinking about the facts of this beautiful and terrible world and their underlying causative links.
In the preceding section we recited the scientist's catechism, of the great importance and utility of Ockham's Razor. It may come as a surprise to our colleagues that not everyone agrees. For instance, in a remarkably perceptive article, Oreskes, Shrader-Frechette, and Belitz write:[20]
Ockham's razor is perhaps the most widely accepted example of an extraevidential consideration. Many scientists accept and apply the principle in their work, even though it is an entirely metaphysical assumption. There is scant empirical evidence that the world is actually simple or that simple accounts are more likely than complex ones to be true. Our commitment to simplicity is largely an inheritance of 17th-century theology.
Now that puts us right into our place, in the company of ancient priests!
Though this quote cuts to the heart of the problem, we would prefer to approach the difficulties with Ockham's Razor gently, through several chemical examples. And since this is a dialogue, with epistemological intent if not expertise on the part of its authors, we will wend our way back eventually to a balanced view of this principle.
Continuation of the story of the mechanism of inversion of configuration at tetrahedral boron provides the first example. When, in due time, a sufficient body of experimental and computational data had been accumulated concerning the intrinsic mechanisms governing inversion of configuration at a variety of tetrahedral main group metal centers,[21] unequivocal evidence was presented for the simultaneous operation of at least three of the forementioned mechanisms, including the one rejected ostensibly on the basis of Ockham's Razor. Each mechanism has precisely the same net outcome, namely inversion of stereochemistry at the main group metal center. The relative contribution (or energetic preference) of a given mechanism depends on the metal. Structural factors influence the mechanism as well, and may be deliberately manipulated. In some cases (e.g., complexes of zinc and cadmium) all three mechanisms are virtually equivalent in their energetic demands.
Such a diversity of reaction paths for one and the same chemical transformation is by no means a unique occurrence. With rapidly developing experimental and computational techniques for studying reaction mechanisms, a good number of important chemical reactions have been found to follow several competing reaction channels, their relative significance sometimes critically dependent on most subtle variation of structure and reaction conditions. This relatively new development may be illustrated by just a few examples.
Consider first a classic pericyclic reaction,[22] the Cope rearrangement (3,3-sigmatropic shift; Fig. 2). Here, even rather tiny structural tuning of the parent hydrocarbon, 1,5-hexadiene, appears to lead to a switch from the most typical pathway (a) with its 'aromatic' transition state structure (in two isomeric forms), to pathways (b) or (c), which feature, respectively, a biradical-like transition state or an intermediate.[23] We will return below to the current state of affairs in this mechanism.

Figure 2. Three mechanisms for the Cope rearrangement.
As a second example, let's look at a challenging current mechanistic problem, that of unraveling the mechanism of formation of fullerenes, the polyhedral products of graphite vaporization at plasma temperatures of over 3 000 °C. Contrary to an 'entropic' expectation of the existence at these conditions of structurally little-organized forms of matter, specific, highly symmetric polyhedral C2n molecules, their structure reminiscent of the geodesic domes exploited in architecture by R. Buckminster Fuller, are created in carbon vapor. C60, possessing the truncated icosahedral geometry of a soccer ball, has attracted special attention because of the perfection of its polyhedral structure, its relative stability, and the horizons opened up with the discovery of a new allotrope of carbon.
How does this thermodynamically unstable molecular soccer ball assemble? Considerable effort has been expended on detailed study of the mechanistic aspects of fullerene formation following graphite vaporization.[24] Several ingenious suggestions for the growth process that generates the C60 have been forwarded.[25] Yet a tiny deviation from optimal reaction conditions found in the famous pulse laser vaporization experiment of Smalley, Curl, Kroto and coworkers appears to result in a drastic decrease of the yield of C60, and in alteration of the mechanism of self-assembly of carbon atoms as well. R. Smalley, one of the discoverers of fullerenes says: "Of course, there must be hundreds of mechanisms whereby a fullerene like C60 can form".[26] Smalley's statement, with which we agree, by no means signifies a repudiation of attempts to gain insight into the detailed mechanism and the driving forces of the spontaneous self-assembly of carbon atoms. The statement merely emphasizes the great complexity of the problem, and the terrible incompleteness of our knowledge.
The greater the insight gained into the origin of chemical transformation, the more justified seems the view that reaction pathways are inherently manifold. As we said, one usually thinks of a chemical reaction as a geometric rearrangement of the relative positions of the nuclei which make up the interacting molecules, i.e., motion along a path on the potential energy surface (PES), bisected by ridges that form the reaction barriers. Such a picture of a PES reminds one of a hilly landscape; the metaphor continues with the successfully transformed molecule likened to the motion of a mountaineer moving from the valley of reactants to that of products by surmounting one of the lowest possible passes.
But the real hilly landscapes of this world (or those calculated) are not so monotonous as to feature a unique pass between valleys. Thus branching of reactive trajectories might be a rather common occurrence. The number of trajectories grows rapidly when reactants are supplied with an additional increment of kinetic energy. The requirement of passing through a single saddle point is then relaxed. Moreover, when the nuclear displacements in the course of rearrangement of reactants to products are sufficiently small, the reaction may proceed by a kind of trickling through (under) the energy barrier, i.e., by quantum mechanical tunnelling.[27]
Let us continue our fault-finding with Ockham's Razor:
Supposing there are two explanations for a phenomenon or an observable. Let's symbolize one as
(1) P = A
where A is the determining factor. The other explanation can be written symbolically as
(2) P = ca A + cb B
i.e., is viewed as being caused by two factors, A and B, in some admixture.
Now it may be that for a single observable P the 'simple' explanation (1) made good enough sense of the available data, and by Ockham's Razor would be preferred to (2). But the universe is likely to have in it not one phenomenon or observable P, but several, P1, P2, P3 ... Adducing the more complex explanation (2), even when only one of these phenomena is known, may lead to the eventual realization that there is some related one, P2. The more complex explanation is productive, it leads one to think about alternative experiments.
Such an approach may be thought of as one formalization of the epistemologic method of multiple hypotheses that had been advanced at the beginning of this century by Chicago's geologist T.C. Chamberlain and later used by J. Platt (a one-time physicist and chemist) as the basis for the 'method of rigorous conclusions'.[28]. These methods, in a way ramifications of F. Bacon's seminal method of induction, point to the fact that to achieve the right conclusion, simultaneous testing is needed of several hypotheses, each endowed with its own means of uncovering the truth. The summary result of the application of various means and approaches must be richer (and more complete) than the relentless pursuit of any single hypothesis. Do we need to rehearse the myriad examples the history of chemistry (or our colleagues) provides of the sterility of hypotheses held too strongly, too single-mindedly, by individuals?
To finish the argument against the trivial application of Ockham's Razor:
Time and time again the process of discovery in science reveals that what was thought simple is really wondrously complicated. If one can make any generalization about the human mind, it is that it craves simple answers. This is true in politics as in science. So we have a President of the USA (pick any recent one) saying that if we control the flow of drugs across our borders, then we will diminish greatly the terrible social problem of drug addiction. Or, just to take something from across the political spectrum, someone (no President would dare) asserting that if we distribute condoms in the schools that such action will reduce significantly the spread of AIDS.
The ideology of the simple reigns in science as well, whereas every real fact argues to the contrary. So we have the romantic dreams of theoreticians (e.g., Dirac) preferring simple and/or beautiful equations. The intricacy of any biological or chemical process elucidated in detail points clearly in the opposite direction.
Let us be specific here, with a chemical and biological vignette: the story of the sex pheromone of the cabbage leaf looper moth, Trichoplusia ni. When the pheromone was first discovered in 1966, it was thought to be a simple molecule, (Z)-7-dodecenyl acetate. A few years later a second active ingredient was found, and more recently some clever biosynthetic reasoning by Biostad, Linn, Du and Roelofs led to the discovery that a blend of six molecules was needed for full biological activity.[29] There is a relationship between the concoction of a new perfume and insect chemistry.
It is not that every physical, chemical, or biological observable needs to have a complicated cause. But we would argue that in the complex dance of ingenuity that is modern science, in the gaining of reliable knowledge, one should beware of the inherent weaknesses of the beautiful human mind. The most prominent shortcoming is not weak logic, but prejudice, preferring simple solutions. Uncritical application of Ockham's Razor plays to that weakness. What is worse, it dresses up that weakness in the pretense of logical erudition.
We have fleshed out the argument against the use of Ockham's Razor in science. But now it is time to reverse gears, and argue the other way.
In our guise as critics of Ockham's Razor, we are, perhaps, guilty of pulling off a philosophical sleight of hand. We (and other critics) imply a necessary relationship between the preference for a simple model and the belief in a simple universe. We then go on to argue that the universe is hardly simple, and thereby appear to invalidate the application of Ockham's Razor in scientific investigation. But does it really follow that one must believe in a simple universe in order to be philosophically honest when invoking Ockham's Razor? Is it not inherent in any analytical epistemology, that one attempt to find simple intellectual bricks from which the wonderfully complex architecture of Nature could be reconstructed? And isn't it really the case that Ockham's Razor properly applies to the identification of these individual modules, rather than to the entire Weltanschauung that one builds from them? The principle of parsimony is not a metaphysical statement about the way the universe is. Everyone knows it is wondrously complex, Ockham's Razor is a prescription for unraveling and comprehending - piece-wise, never completely - its marvelous complexity. In this pragmatic point of view, Ockham's Razor serves as an operational principle, not a rule or a Law of Nature.
In the so-called 'scientific method', we seek to devise experimental tests that can falsify our hypotheses. The excommunication of ideas that takes place when a model 'fails' one of these trials is taken to be rigorous and irreversible, provided that the experimental tests meet criteria of both intellectual validity and competence of execution, therefore reproducibility.
In the pragmatic interpretation of Ockham's Razor, one would not use such irrevocable language. One might say that the choice between two otherwise equally valid models should be made in favor of the simpler, but that the rejection of the more complex is only conditional. The idea that has been set aside could be reconsidered at a later date if the currently favored hypothesis fails some future test. If one adopts such a view, it follows that the temporarily discarded model should not be said to be 'ruled out' by or to have 'violated' Ockham's Razor, since this language belongs in the domain of the more rigorous exclusionary tests.[30]
But even this liberal prescription for the use of Ockham's Razor begs the underlying question of 'why?' Why should we lean in favor of the simpler of two otherwise equally satisfactory models? We can advance several arguments, no one of which has logical rigor beyond an appeal to reasonableness.
1. The simpler model is likely to be more vulnerable to future falsification, because with fewer adjustable parameters it will have less flexibility. If, as Popper suggests, a good scientific hypothesis is one that is falsifiable, then perhaps the better of two competing models is the one that is somehow more falsifiable. To be vulnerable is not a weakness, in science or human relationships.
2. Or one could say that the simpler model provides a clearer and more readily comprehensible description. This view would admit the human difficulty with handling complexity, and relate simplicity to comprehensibility. It is important to understand, and the breaking of a complex reality into comprehensible bits is not only the Cartesian method, but a teaching strategy.
3. A third rationale relies on an assessment of the probability of future success of any model. Suppose, in some experiment, we made a series of measurements of a property y in its response to adjustment of a factor x, with results depicted in Figure 3.
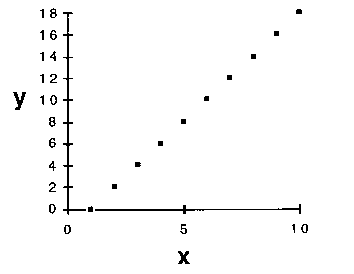
Figure 3. Some experimental measurements of a property y
in response to variation of a factor x.
If one wanted to try to describe y as some mathematical function
of x, one would probably choose a straight-line relationship (Fig.
4a) in preference to a more complex functional form such as that shown
in Figure 4b.
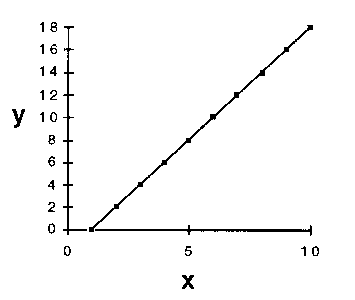 4a
4a 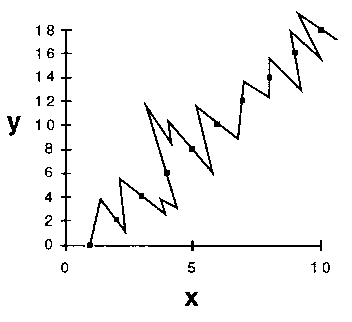 4b
4b
Figure 4. (a) A straight line fitted through the data points of
Figure 3. (b) Another fit of the same data points.
But, aside from some intuitive sense that it just seems right, why would one prefer the straight-line model? An answer can come from looking at the degrees of freedom of the fits. In statistics, the number of degrees of freedom of a model is the difference between the number of independent experimental observations and the number of adjustable parameters in the mathematical function that seeks to describe the relationship between y and x.[31] It is axiomatic that any function with a number of adjustable parameters equal to or greater than the number of observations can be made to pass exactly through all of the (x, y) points on the graph. However, it is not necessarily true that a function with fewer adjustable parameters than the number of observations will pass through all of the points. If it turns out that it does, then the function - our model - has already had some success in describing one or more events that we have measured experimentally.
The number of degrees of freedom of a model can be thought of as the number of points whose positions were correctly described by the model, without any algebraic requirement that it should come out that way. The world is not static. One measurement will be, must be, followed by another. Models that predict are valued. Since we are presumably seeking a mathematical relationship between y and x in order to predict future points on the graph, we are naturally more inclined to choose the model that has already had the greater success in 'predicting' the measurements we have made so far. This will be the model with the larger number of degrees of freedom, or the smaller number of adjustable parameters - i.e., the simpler model.[32] [33]
4. The graphical representation of the y versus x relationship serves to illustrate a fourth, and here the last, reason for applying Ockham's Razor as an operational principle. The number of equally satisfactory models in a given class is generally related to the complexity of the class. For example, there is one and only one straight line that will pass through all of the (x, y) points in the graph described above. We do not have to ask which straight line to choose in order to best represent the x, y relationship. On the other hand, since the number of parameters required to describe the jagged line in the illustration of our more complex model exceeds the number of observations, there exists an infinity of jagged lines, all passing exactly through the points. With the observations made so far, we have no logically defensible way to choose one from this infinity.
To put it another way, if you think Ockham's Razor gets you into trouble by limiting the number of hypotheses, thereby diminishing the imaginative world, then relaxing from Ockham's Razor opens up real, indeterministic, chaos - the infinity of hypotheses that fit.
Those of us who have mystically inclined, nonscientist friends may have used arguments like this last one in our discussions of the lack of general scientific acceptance for extra-sensory perception, UFOs, homeopathic medicine, or astrology. The nonscientist might ask: "Do you scientists think you understand everything about how the universe works?" When we modestly profess our woeful lack of understanding, we might hear in return: "Well then how can you rule out the possibility of ... ?"
Of course the answer is that we cannot, but in order to make any kind of sense of the world, we must have some procedure for selecting among the plethora of ideas that the collective action of creative human minds has spawned. If we had to operate under an equal opportunity clause for every concept that was ever espoused, we would have such an impossibly complex and self-contradictory description of Nature, that we could never feel that we were making progress in understanding or utilizing our environment.
Why should we make progress? Have we progressed? We are painfully aware of all the ambiguities of the 19th century idea of Progress, in which science flourished. And of the deep mistrust of such progress by thoughtful people in our time. While we are actually ready to do battle for progress, not without internal doubts, this is not the place for that confrontation.
The need to have operating principles just to make progress at all in sifting through the complexity of Nature shows up most clearly in the procedure called Principal Component analysis (PCA).[34] [35] [36] Many of the observables of nature are multivariate, i.e., each property or phenomenon analyzed yields a series of numbers. Examples are spectra or chromatograms, yielding a datum for each wavelength or retention time. PCA allows one to correlate the data available by deriving a set of orthogonal basis vectors, principal components, so that the first such component represents the best linear relationship, the one showing the greatest variation exhibited by the data. Each successive principal component explains the maximum variance not accounted for by the previous ones. Identifying the number of significant components enables one to determine the number of real sources of variation within the data. The most important applications of PCA are those related to: (a) classification of objects into groups by quantifying their similarity on the basis of the Principal Component scores; (b) interpretation of observables in terms of Principal Components or their combination; (c) prediction of properties for unknown samples. These are exactly the objectives pursued by any logical analysis, and the Principal Components may be thought of as the true independent variables or distinct hypotheses.
One example of the application of PCA in chemistry may be found in the recent statistical analysis of the concept of aromaticity by Katritzky et al.[37] Widely applied for the characterization of specific features of conjugated cyclic molecular systems, the notion of aromaticity lacks a secure physical basis. Not that this has stopped aromaticity from being a wonderful source of creative activity in chemistry.[38] We can think of no other concept that has led to so much exciting chemistry! Yet, although numerous indices of aromaticity have been designed, based on energetic, geometrical and magnetic criteria, no single property exists whose measurement could be taken as a direct, unequivocal measure of aromaticity.
The PCA analysis of the interrelationship of 12 proposed indices for nine representative compounds indicated that there exist at least two distinct types of aromaticity. 'Classical aromaticity' is well described by certain interrelated structural and energetic indices, whereas the second type of aromaticity, the so-called 'magnetic aromaticity', is best measured by anisotropies in the molar magnetic susceptibility. It seems that the concept of aromaticity should be analyzed in terms of ornate hypotheses, a multiplicity of measures.[39] But notice that the ornate description is reducible to simple components. The universe is not simple, but the models used to describe it can be made of simple pieces.
Several further examples of the power of intelligent PCA may be found in the recent chemical literature. So Murray-Rust and Motherwell [40] have looked at the molecular deformations of 99 b-1'-aminofuranosides, and have shown a very pretty strong correlation with two Principal Components, just those expected to define the pseudorotation of the five-membered sugar ring. An analysis of distortions in five-coordinate complexes by Auf der Heyde and Bürgi [41] showed beautifully the relationship of various modes such as the Berry pseudorotation, a SN2-type mode and an addition/elimination path. And Basu, Gô and coworkers [42] use a Principal Component analysis of molecular dynamics simulations to trace the path of a 310/a-helix transformation in an oligopeptide.
Is there an equivalence between a Principal Component and a physically meaningful factor which, coupled with strong logic, could provide what we usually mean by 'an explanation'? In general not. Yet, as Michael Fisher has pointed out to us, an identification of the Principal Components "can, and often does, lead to deeper theoretical insights and constructs".[43] Fisher points, for example, to the Fourier analysis of the tides, in which Lord Kelvin played a principal role, and which led to an understanding of the contributory factors beyond the gravitational pull of the moon.
Incidentally, there is nothing special about chemistry's problems in identifying causes and fundamentals here - the complexity of this task is illustrated just as well by the difficulties arising in the quantitative description of the perception of quality in food. While from the deterministic standpoint, the quality of a steak or a Bordeaux wine may be decomposed into attributes or components, sensory analysis points to simple words (factors) with a world of meanings used by real people to characterize foods.[44]
The science of statistics incorporates Ockham's Razor in its framework in a number of explicit and implicit ways. A particularly useful methodology for fitting models to data and assigning preferences to alternative models is Bayesian inference, introduced by Harold Jeffreys.[45] [46] We reproduce here a figure (Fig. 5) with its full caption from an important article on Bayesian interpolation by MacKay [47], which succinctly indicates how Ockham's Razor enters the choice of models in this methodology. A further exposition to the method may be found in the very clear article by Jefferys and Berger, entitled Ockham's Razor and Bayesian Analysis.[48]
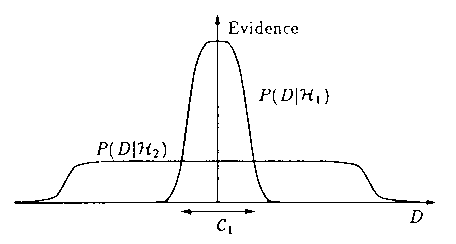
"Why Bayes embodies Occam's razor. This figure gives the basic intuition for why complex models are penalized. The horizontal axis represents the space of possible data sets D. Bayes rule rewards models in proportion to how much they predicted the data that occurred. These predictions are quantified by a normalized probability distribution on D. In this paper, this probability of the data given model Hi, P(D|Hi), is called the evidence for Hi. A simple model H1 makes only a limited range of predictions, shown by P(D|H1); a more powerful model H2, that has, for example, more free parameters than H1, is able to predict a greater variety of data sets. This means however that H2 does not predict the data sets in region C1 as strongly as H1. Assume that equal prior probabilities have been assigned to the two models. Then if the data set falls in region C1, the less powerful model H1 will be the more probable model."
Figure 5. A figure with its caption (from a paper by D.J.C. MacKay [47]), describing how Ockham's Razor influences the choice of models in a Bayesian analysis.
Our dialogue is not over; we return to question the arguments made
in favor of an operational valuation of Ockham's Razor.
If we distance ourselves from philosophical implications by treating Ockham's Razor as just an operating principle, aren't we really displaying intellectual cowardice? Take that straight-line graph (Fig. 4a). If we made the measurements leading to the (x, y) points already shown (Fig. 3), wouldn't we really believe that the 'proper' value of y at some new value of x within the range would be the one that fits on our straight line? Indeed, if we didn't obtain such a result wouldn't we suspect that we had made a mistake in our experiment? And isn't such an expectation really a belief in a simple universe?
In the processing of models we must be especially cautious of the human weakness to think that models can be verified or validated. Especially one's own. The Oreskes, Shrader-Frechette, and Belitz article from which we drew that provocative quote makes this point most convincingly. The main tactical problem in modeling the course of chemical reactions, be they ozone depletion or a pericyclic reaction under new conditions, is to find a reasonable balance between completeness of description of an object or phenomenon under study, and the simplicity of the models applied. The balance is really, really delicate and the razor (Ockham's Razor!) is best wielded by a really skillful barber (experienced chemist) to ensure that essential but hidden features of the object under study were not lost upon modeling its properties and behavior. In the United States, at least, there are not too many barbers left who can give you a razor shave.
The dialogue is not finished. When one infers a linear relationship from empirical observation, be it a linear free energy relationship in physical organic chemistry, or a Hooke's Law relationship in physics, one would indeed be surprised if some of the measurements, made within the range of all the others, failed to fit the model. But that surprise derives not from belief in a simple universe, but rather from belief in a smoothly changing one. With the important and fascinating exception of systems on the threshold of chaotic behavior,[49] or those near phase transitions, our experience suggests to us that the universe is much more a system of smooth curves than jagged edges. It is not often that small changes in some control factor cause wild and unpredictable swings in the response of the system under study. We understand now the importance of bifurcation points in chaotic systems, and know that complex assemblies are subject to chaotic behavior. But most of chemistry is a science of smooth trends. While nobody believes that the plot of free energy of activation vs. standard free energy of reaction is well described by a straight line for all reactions, we can restrict our attention to small enough changes in the structures of the substrates so that the smooth relationship between activation and reaction free energies can reasonably well be approximated by a straight line.
Take that Cope rearrangement again (Fig. 2). For a while it looked like the compromise between the 'aromatic' and 'biradical' camps was to say that both were right, and that the system flipped from one mechanism to another in response to changes in substituent, as we have described. Such a flip-flop would not be easily described by any linear or smoothly curved function. However, the latest, highest-level ab initio calculations have returned us to a smoother description.[50] The multiplicity of reaction channels has disappeared again, and we are now in a situation where the best model seems to be one in which the geometry of the transition structure moves smoothly and continuously from 'aromatic' to 'biradical' in response to substituent changes.
Even the duality of 'concerted' vs. 'stepwise' mechanisms may be falling to a smoother description. The forced choice between such descriptions is, at least in some cases, a consequence of drawing a potential energy profile in which there is only a single dimension assigned to the reaction coordinate. One then has only two options: one includes a little dip in the curve to imply the existence of an intermediate along the reaction coordinate (stepwise), or one does not (concerted). But of course, for a nonlinear, N-atom molecule there are 3N - 6 dimensions to the reaction coordinate. In this space, there is no need to place a local minimum in the potential energy surface on an obligatory path between reactant and product. If such a local minimum exists, and if it is energetically accessible without intervening barriers, then should it be called an intermediate or not? Is the reaction concerted or stepwise? The two descriptions merge smoothly together.[51]
Some barbers will use Ockham's Razor to give you a smooth shave.
Three final comments in this discussion, neither pro nor con ...
1. The gap between the complexity of an object under study and comprehension of its origin is bridged (shaky constructions, to be sure ...) through elaboration of suitable models devised to describe the underlying features of the object under study in terms of previously understood phenomena. Every model is, by definition, incomplete.[52] It is thus hardly surprising that a set of complementary models, each of them valid over a certain range of application, is generally needed to describe adequately an object as a whole.
We forward a tentative notion that in the evaluation of models, different criteria may be applied whether one seeks understanding or predictability. We enter an epistemological battleground here (deep trenches recently dug on the field of artificial intelligence ...) in positing that there is a difference between human understanding, perforce qualitative, and that dream of dreams, a computational model that predicts everything accurately.[53]
Real chemical systems, be they the body, the atmosphere, or a reaction flask, are complicated. There will be alternative models for these, of varying complexity. We suggest that if understanding is sought, simpler models, not necessarily the best in predicting all observables in detail, will have value. Such models may highlight the important causes and channels. If predictability is sought at all cost - and realities of the marketplace and judgments of the future of humanity may demand this - then simplicity may be irrelevant. And impossible, for, as we said, any real problem is complex and will force a complex model. Whatever number of equations or parameters it takes, that's fine. As long as it works.
2. Ockham's Razor is a conservative tool. It cuts out crazy, complicated constructions and assures that hypotheses be grounded in the science of the day. So the tool is certain to lead to 'normal' science, the paradigmatic explanation. Revolutions in science, to follow Thomas Kuhn's fruitful construction, do not grow from such soil.
Perhaps that is an oversimplification. At the critical turning point when a revolution is about to break loose, Ockham's Razor can turn a conservative into a reluctant revolutionary. We are thinking of Max Planck, interpolating between the Wien and Jeans radiation laws, and following the logic, an Ockham's Razor logic, to the quantum hypothesis. And, it seems, resisting that hypothesis even as the world and he found it necessary.[54]
3. The search for true understanding might be compared with the crafting of an endless, absorbing mosaic picture. The pieces already in place, lustrous and dull, have been laboriously and joyously shaped in the creative work of thousands of years of protoscience and a few hundred of 'real' Western science. They furnish us with some clues as to the nature of the beast. If simplicity of interpretation (in other words, "beauty of equations", according to P.A.M. Dirac, or "lucidity complementary to truth", according to Niels Bohr) be a desirable quality, the interpretation must be constructed out of simple [55] components. The principle of parsimony is then just what we need as we labor, discover, and create.
If the desideratum be a human science open to change and the unexpected, then maybe there are occasions when Ockham's Razor should be sheathed. Or we should remind ourselves ceaselessly of the conditional interpretation of a conclusion based on Ockham's Razor reasoning. Cognizance of the complexity that so beautifully contends with simplicity in this evolving world, cognizance of the creative foment of intuition without proof within science, lead us to think so.
Intuition serves us as we argue for a certain sterility of William of Ockham's sharp principle. And the same concept, intuition, figures prominently in the strong pull on us toward the simple, the logical, and the beautiful. Plato had that right. 'Intuitive' is, probably, the best characterization of the law of parsimony, Ockham's Razor. It is also intuition that sometimes leads to the oh so many blind alleys, if not mistakes, of our sciences. And it is precisely human intuition that provided and provides for the disclosure of those mysterious and wondrous ways of Nature, and the creation of so much new. The mosaic grows.
We are grateful to many friends for their comments on this paper, and for leading us to further information. These include Alexandru Balaban, Jerome Berson, Robert Crabtree, Jack Dunitz, Michael Fisher, Eva Hoffmann, Hillel Hoffmann, Norman Kretzmann, Mary Reppy, Einar Risvik, Brian Tierney, Frank Westheimer, and L. Pearce Williams.
* This is a slightly abbreviated version (abbreviation by J. Schummer) of a paper originally published under the same title in: Bulletin de la Société Chimique de France, 133 (1996), 117-130. Republished with the permission of Elsevier, Paris.
Copyright Ó1996 by Elsevier, Paris