Mathematical Chemistry!
Is It? And if so, What Is It?
Douglas J. Klein*
Abstract: Mathematical chemistry entailing the development of novel mathematics for chemical applications is argued to exist, and to manifest an extremely diverse range of applications. Yet further it is argued to have a substantial history of well over a century, though the field has perhaps only attained a degree of recognition with a formal widely accepted naming in the last few decades. The evidence here for the broad range and long history is by way of numerous briefly noted example sub-areas. That mathematical chemistry was only recently formally recognized is seemingly the result of its having been somewhat disguised for a period of time – sometimes because it was viewed as just an unnamed part of physical chemistry, and sometimes because the rather frequent applications in other chemical areas were not always viewed as mathematical (often involving somewhat ‘non-numerical’ mathematics). Mathematical chemistry’s relation to and distinction from computational chemistry & theoretical chemistry is further briefly addressed.
Keywords: mathematical chemistry, physical chemistry, computational chemistry, theoretical chemistry.
1. Introduction
Chemistry is a rich and complex science, exhibiting a diversity of reproducible and precisely describable predictions. Many predictions are quantitative numerical predictions and also many are of a qualitative (non-numerical) nature, though both are susceptible to sophisticated mathematical formalization. As such, it should naturally be anticipated that there is a ‘mathematical chemistry’, rather likely with multiple roots and with multiple aims. Mathematical chemistry should focus on mathematically novel ideas and concepts adapted or developed for use in chemistry (this view being much in parallel with that for other similarly named mathematical fields, in physics, or in biology, or in sociology, etc.). This definition distinguishes mathematical chemistry somewhat from simple routine mathematics for chemical problems and even from rather complex mathematics used repeatedly in some standardized manner (perhaps in the form of a ‘canned’ computer program). Further refinement of the idea of ‘mathematical chemistry’ is then of natural interest.
It is perhaps not surprising that ‘mathematical chemistry’ has come to be so named, two journals inaugurated, and a society founded, all with much research activity having occurred. Indeed much of this activity is evident from: Rouvray’s editorial forward (1987, for the first issue of the Journal of Mathematical Chemistry); Löwdin’s (1990), Mackey’s (1997), and Mallion’s (2005) commentaries on what ‘mathematical chemistry’ should become; Trinajstić & Gutman’s (2002), King’s (2000), Haberditzl’s (1979), and Balaban’s (2005) presented ‘reviews’ of the field; as well as a few briefer commenting letters (Pauling 1987, Prelog 1987, Karle 1987). And yet further there are related relevant comments (Thomson 1918, Primas 1983, March 1983, Laughlin 2000) on the connection and interaction between chemical theory and physics as well as mathematics. Most all of these earlier works focus on some special recently developed area within mathematical chemistry, and thereby typically leave a biased view of the field as a whole. A few of the letters or shorter articles, while making a general definition, however describe and illustrate the field so briefly that the full richness of the field is not clearly perceived. And yet further some of the articles seem to indicate that mathematical chemistry has only been born within the last two or three decades.
Thence a more comprehensive view of ‘mathematical chemistry’ seems called for and is here attempted, seeking to indicate the full range and long history. Though the support for this view is found to be difficult to clearly and fully achieve, the current presentation is far more complete than that in the few earlier mentioned articles, which seem often to agree in the formal definition, yet omit mention of sizable portions of the field perhaps giving only a few very narrowly selected examples, often also limited to rather recent decades. Here emphasis is placed on the field’s breath-taking broadness and long history of well over a century. The contrast to several earlier reviews is evident because the field of mathematical chemistry appears to have been somewhat ‘disguised’, at least for a period of time, with then huge portions simply unmentioned in several of the earlier reviews. The support for the present view of strength and history is documented here by way of a listing of around two dozen sub-areas of chemical research, each illustrated with a modest (incomplete) selection of representative publications (see Appendix), which are arguably part of mathematical chemistry. Some earlier contributions are merely alluded to by way of a few important names, while the explicitly identified publications are largely focused within the last 100 years. The various identified researchers, books, and articles variously exhibit the use (or proposed use) of novel mathematical ideas in application to chemistry. Thence a more balanced, a more truthful, and more comprehensive view of the full field of mathematical chemistry is attained.
2. Mathematical Chemistry Detailed
Again, mathematical chemistry focuses on mathematically novel ideas and concepts adapted or developed for chemistry. The mathematics may be from any of many diverse mathematical areas, including: differential equations; partial differential equations; group theory (geometric or not); Lie algebras; combinatorics; graph theory; the theory of partially ordered sets and lattices; linear algebra and matrix theory; probability theory and statistics; number theory; algebraic and combinatorial geometry; topology; functional analysis; Von Neumann and C* algebras; rigged Hilbert spaces; homological category theory; fundamental logic and meta-mathematics; and more. That is, there is no a priori reason to exclude certain areas of mathematics, though some areas might naturally prove more fruitful for chemistry.
Overall there are very many non-trivial chemical applications of novel mathematics from each of the broad chemical ‘fields’ of analytical, inorganic, organic, biochemical, and physical chemistry. But such work viewed as part of mathematical chemistry is here illustrated at a finer scale of narrower chemical ‘areas’, as now are listed:
- Foundational equilibrium thermodynamics was begun long ago in a mathematical mode, e.g., by A. Avogadro and H.L. LeChatelier and most especially by R. Clausius, then also by J.H. van ‘t Hoff, W. Ostwald, S. Arrhenius, J.W. Gibbs, W. Nernst, F. Haber, and G.N. Lewis. This early work received several Nobel prizes. More recently there are many more examples of mathematical researches, by M.E. Fisher (1972) and B. Widom (1965 and 1974) on critical-point scaling related to critical-point exponents (as further clarified with renormalization-group Nobel-prize-winning arguments of K. Wilson, and others, mostly in physics). Yet also there is F. Weinhold’s (1975a,b,c,d) development of a geometric Riemannian metric for thermodynamic manifolds, and there are many other results. (For references, see Appendix 1.)
- Equilibrium statistical mechanics was also begun a little over a century ago by Gibbs and many others (often physicists, like Maxwell and Boltzmann), all in a highly mathematical mode. Later (mathematical) developments arise with J. Mayer’s (1938a,b) and others graphical cluster expansions for statistical-mechanical thermodynamic properties, with E. Montroll’s (1941) powerful transfer-matrix methodology for the solution of partition functions when interactions are ‘local’, and with Lars Onsager’s (1944) mathematical tour de force (transfer-matrix) solution of the 2-dimensional Ising model. And still there is much further ongoing activity, though there is much more also. (For references, see Appendix 2.)
- Electrochemistry has an even longer history dating back to H. Davy, M. Faraday and G. Kirchhoff. (Especially Kirchoff’s work is accepted as mathematical, while the mathematically uneducated Faraday ended up founding ‘field theory’.) More recent mathematical contributions are encountered with P.W. Debye and E. Hückel (1923a,b) in their theory of ionic solutions (and activity coefficients), or with R. M. Fuoss and L. Onsager (1957) and others in the theory of conduction in ionic solutions, or with R. Marcus (1956, 1965, 1977, 1993) in his Nobel-Prize winning work on structure-mediated charge transfer. Yet further there is important work on electrochemical processes, and a recent interest in molecular electronic conduction, particularly for application in nano-devices. (For references, see Appendix 3.)
- Chemical kinetics dating back to the 19th century has been pursued more recently in terms of many different example cases. Some such are found with the various (mathematical) modelings of the Belousov-Zhabotinsky reaction (as a prototypical complex spatio-temporally oscillatory case), or with Ilya Prigogine’s work in this general area, for which there was awarded a Nobel prize. A notable development is M. Eigen (1971) and others mathematical characterization of ‘evolution-complicit’ hyper-cycles. Also, there is work by L. Peusner (1986) and others on ‘network thermo-processes’, or Clark’s work on reaction-diffusion processes, or more recent extensive work concerning chaotic reaction dynamics, as reviewed by Scott (1991) and Rice et al. (2005). (For references, see Appendix 4.)
- Non-equilibrium thermodynamics, beyond chemical kinetics and ordinary diffusion, this area has many contributions by physicists, but also includes Lars Onsager’s (1931) Nobel-prize winning development of his reciprocal relations amongst thermodynamic response functions. More recently there are various (mathematical) works developing the quantitative dynamics of entropy-production particularly in the linear-response regime approaching equilibrium, and there is Prigogine and Henin’s (1969, 1973) radical subdynamics, and yet further Ernst Ruch’s (1975, 1992) work on his fundamental partial-ordering ‘structural principal’ which concerns complementarities of distinction/identity and of order/disorder. (For references, see Appendix 5.)
- Spectroscopic theory with a strong mathematical flavor developed enormously during the 20th century, with foundational work on rotational, vibrational, rovibrational, vibronic, and electronic spectra, as well as molecular excitonic spectra, electron-spin resonance, and nuclear magnetic resonance. The Nobel prize to G. Herzberg was for (implicitly mathematical) deductions from electronic spectra of features of electronic potential curves or surfaces. With the availability of suitable high-performance electronics there has further followed mathematical (and experimental) development of general Fourier-transform, multi-photon, nonlinear, and multi-dimensional spectroscopies (which indeed have garnered a Nobel prize). Further there are different (e.g., mass) spectroscopies based on other than electromagnetic waves. (For references, see Appendix 6.)
- Mathematical crystallography developed classically with the identification of the Bravais lattices and crystal classes, followed by the seminal identification of crystallographic space groups by Schoenflies and Fedorov. More recent mathematical work is nicely exemplified by Shubnikov and co-worker’s colored crystals (Shubinikov & Belov 1964), by the network descriptions of Wells (1954a,b, 1972) and others, and for the theory of quasi-crystals by Mackay (1975, 1982), Penrose (1978), and others (with a Nobel prize going to D. Schectman, for his ‘recalcitrant’ experimental identification of these). An especially nice (and extremely useful) pure mathematical development is that of J. Karle and P. Hauptmann (1953, 1957a,b, 1960), who shared a Nobel prize for their joint work on the inversion of x-ray scattering data to crystal structures. (For references, see Appendix 7.)
- Diffractive methods include both electron and x-ray diffraction methodologies, and in application to (the common case of) crystals has much overlap with mathematical crystallography. L. Pauling received a Nobel prize in chemistry for his deduction of the alpha-helix structure of proteins, while earlier (Nobel-prize-winning) work is usually viewed as part of physics, though there have been at least three further Nobel prizes in applications to molecules of biologic importance, with the theoretical (mathematical) deductions here being central. Further work on the interpretation of molecular or electron scattering may be viewed to be related (and rewarded with a couple Nobel prizes). (For references, see Appendix 8.)
- Ab initio quantum chemistry developed following the founding of quantum mechanics (in physics), though ultimately the development of computer technology also played a central role. Mathematical work includes Roothaan’s (1951) and Hall’s (1951) development of a (discretized) matrix-based SCF theory, many-body perturbation theory building thereon, facile orbital development numerous molecular-integral evaluations, the theory of reduced density matrices (and associated natural orbitals) by P.O. Löwdin (1955) and others, J. Čížek’s (1966) powerful coupled-cluster method, the development of a promising quantum Monte Carlo technology, and rather numerous other developments, with an evident cap-stone in the overall field being extensive program realization, for example, with J. Pople’s Nobel-prize-winning efforts. (For references, see Appendix 9.)
- Density functional theory, which computes from just the electron density, is viewed by many as part of ab initio quantum chemistry, with early work (by L. Thomas, E. Fermi, J. C. Slater, and others) primarily in physics. Work in the field was carried into chemistry in a general formal mathematical mode with Mel Levy’s (1979) and many others’ proofs and clarifications of fundamental aspects, initiating with the (Nobel-prize-winning) work of W. Kohn and co-workers. But especially significant is a marriage with classically based chemical electronegativity and hardness/softness ideas, all as seminally reviewed in Parr and Yang’s (2000) text. Again there is a cap-stone of extensive program development. (For references, see Appendix 10.)
- Group-theoretic methodology, mostly following the advent of quantum mechanics (detailed in early summary works of Weyl (1928), Wigner (1931), and Yutsis et al. (1962)) includes work on the symmetric group (of permutations) by F.A. Matsen (1964), I.G. Kaplan (1975), and others, then work on the unitary group by J. Paldus (1974, 1975) and others, and yet further work on general Lie group (or Lie algebraic) uses by C. Wulfman and others. With a more classical geometric scope there is much work on point groups, indicated in F.A. Cotton’s (1963) popular text, and also note the extensive development of ligand-field theory. Further there is work on alternancy (or particle-hole) symmetries, on color symmetries, on generalizations thereto, and finally on non-rigid-molecule groups. (For references, see Appendix 11.)
- Molecular dynamics concerns the quantum mechanical characterization of the motion of nuclei, as in Wilson et al.’s seminal book (see Appendix 5), and it is further nicely exemplified with the Jahn-Teller (1937) effect, with H.C. Longuet-Higgins’ phase (more often termed the ‘Berry’ phase), and with A.D. Liehr’s (1963a,b) related elegant characterizations. More recently there is R.D. Levine and R.B. Bernstein’s (1973) development of very broadly useful information-theoretic ‘surprisal’ methods. There is much work with conceptual import (as of reaction paths or of semi-classical ideas), related characterizations of potential energy hypersurfaces, and much work on molecular scattering, as well as some work on ‘chaotic’ dynamics. (For references, see Appendix 12.)
- Solid-state chemistry has much overlap with crystallography and further is perhaps dominated by the enormous amount of work in solid-state physics. Still there are numerous mathematical chemical articles (by chemists) including H.C. Longuet-Higgins (1959) and L. Salem’s work on Peirels distortions, and J.A. Pople and S.J. Walmsley’s (1962) development of solitonic excitations, to be followed up by seminal work on these topics by Su, Schreiffer, and Heeger (1980) (with this work as applied to further experimental work on polyacetylene and other organics associated to a Nobel prize for A.J. Heeger, H. Shirakawa, and A.G. MacDiarmid). There is further mathematical work on molecular excitons, on Burdett’s characterizations of band structure, and on yet other notable aspects of solid-state theory. (For references, see Appendix 13.)
- Stereochemistry has a long history back beyond Van ‘t Hoff and LeBel, and is related closely to some previous noted areas. But also this area includes Pauling’s (1931) fundamental molecular geometric hybridization rules, informative analyses of inversions or internal rotations or pseudorotations (as in cyclopentane), and Lipscomb’s (1958, 1973) Nobel-prize winning work as well as that of others treating boranes (as a prototypical case manifesting the effects of non-classical bonding) and related novel structures. Also there is continuing work with isomers, with molecular geometry characterization, with the Ruch-Schönhofer (1970) chirality characterization, with degrees of achirality and asymmetry, with extensions of chirality characterizations, with molecular shape, and with molecular knottedness. (For references, see Appendix 14.)
- Polymer statistics concerns the conformation-mediated and structure-mediated properties of polymers (especially high polymers), with foundational mathematical chemical (Nobel-prize-winning) work both by P.J. Flory (1953, 1969) and by P.G. DeGennes (1979), particularly as to the manner of polymer size-scaling as a function of their length, and other control parameters. Monte-Carlo methods have been developed and have proved useful. But there are many further mathematical approaches. Also, the field has further blossomed with the development of dendrimers, supramolecular structures, and other large-scale morphological characterizations. (For references, see Appendix 15.)
- Chemical reaction-network analysis, though long around in an informal mode in synthetic organic chemistry, has systematically (and thence mathematically) been developed to elucidate organic synthetic strategies in the work of the groups of E.J. Corey (Corey et al. 1974, 1977), J.E. Dubois (1973), T. Wipke (Wipke & Rogers 1984, Wipke & Vladutz 1990), J.B. Hendrickson (1976, 1986), I. Ugi (Ugi & Gillespie 1971, Dugundji & Ugi 1973), N.S. Zefirov et al. (2002), S. Fujita (2001), P.J. Stadler et al. (1995, 1996), and of several others. Recently there is rather intense effort toward a general theory of ‘complex networks’. And there is work on the mathematical characterization of special reaction-network graphs, as of degenerate rearrangements or of substitution reactions (which mathematically form a partial ordering). (For references, see Appendix 16.)
- Chemical nanotechnology has recently emerged as an interesting and greatly burgeoning separate field, following the development of carbon nanotubes and focused on organic syntheses of novelly interconnected nanostructures; there being notable theoretical work and different mathematically oriented articles, some concerning general theory. As examples for particular nanostructures, there are considerations of nano-knots, nano-links, nanotubes, their caps, nano-tori, nano-cones, nano-belts, Möbius nano-strips, and various negatively curved structures, and yet further there are more elaborate molecular devices, such as molecular motors. Most recently there is incredible activity (with reviews) concerning graphene (including a Nobel prize). (For references, see Appendix 17, Sumners 1988 in Appendix 15, and Flapan 2000 in Appendix 14).
- Semi-empirical quantum chemistry includes Pauling and Wheland’s classically related resonating valence-bond theory, with many more recent developments, as reviewed in various chapters by Klein & Trinajstić (1990), Cooper (2001), and Shaik & Hiberty (2007). Also there is the ‘alternative’ molecular-orbital approach with much mathematical work by E. Hückel (1931), Charles Coulson, H.C. Longuet-Higgins (1974a,b,c,d,e), E. Heilbronner, and many colleagues achieving fundamental Hückel-model-based theorems for the case of conjugated pi-electron networks. Besides ligand-field theory already mentioned (under group theory) there is Woodward and Hoffmann’s Nobel-prize winning orbital-symmetry conservation rules for concerted reactions (Woodward & Hoffmann 1965a,b, 1970, Hoffmann & Woodward 1965), and K. Fukui’s (Nobel-prize-winning) work concerning frontier orbitals, though also there are many other important results. Parr’s (1964) survey book nicely reveals a gradation between this field and ab initio quantum chemistry. (For references, see Appendix 18 and Coulson 1940 in Appendix 11).
- Structure generation and enumeration is addressed in G. Pólya’s (1937) foundational combinatorial theory of enumeration under group-mediated equivalences – all, in fact, developed to enumerate chemical isomers. Now there are various refinements and extensions, regarding alternant formulations, subsymmetry classification, reaction-mode enumerations, Balasubramanian’s (1981, 1985, 1993) non-identity irreducible-representation enumerations, property characterizations, and comprehensive structure generations. It is argued by Bytautas & Klein (1998) that this field relates intimately to the idea of chemical nomenclature. Much of the mathematics (up to about 1986) is reviewed in Read’s discussion (Pólya & Read 1987), and A. Kerber makes a more comprehensive mathematical survey (and a more chemically oriented, more concise survey in a special issue of MATCH). (For references, see Appendix 19.)
- Physical organic theory is typically defined in terms of the (‘physical’) measurements considered, but it might arguably be better defined as the area dealing with the quantification of the idea of ‘functional groups’ in organic chemistry. Work goes back over a century to deal with constitutional additivities for enthalpies, magnetic susceptibilities, and other (physical) properties. There is also extensive theoretical work on ‘linear free energy relationships’, and the area overlaps extensively with a few others already mentioned. (For references, see Appendix 20.)
- Chemical classification includes the long-standing area of chemical nomenclature, with cap-stone formalizations (which then are implicitly mathematical) available from IUPAC. But there are also the classifications into: categories of chemical bonding (and its mediation by electronegativities and hardnesses); different functional-group classes; different isomer classes; families of elements in Mendeleev’s periodic chart; classes of ‘acid’ and ‘base’; and different classes of ‘aromaticity’. Much of this merges into chemical nomenclature. Also note that much of this classification can be elegantly viewed mathematically in terms of ‘partially ordered sets’. (For references, see Appendix 21, Mislow 1977 in Appendix 14 and Ugi et al. 1970 in Appendix 14).
- Chemo-metrics and QSAR have roots back into the 19th century, though these namings are more recent. The field has recently extensively developed with systematic statistical methodology in drawing correlations (e.g., with consideration of a variety of multivariate regression techniques, sometimes developed in a purely chemical context). There has been an immense development of a diversity of different sorts of available quantities (which can be other experimental properties, quantum-chemically computed characteristics, or simply molecular graph invariants) so as to make structure/property or structure/activity correlations, such as involved in toxicity evaluations, and particularly in drug design. (For references, see Appendix 22.)
- Molecular biology extends classical biochemistry to deal with larger molecules: enzymes, proteins, DNAs, and RNAs. There are then many fundamental theoretical works dating back over half a century, with a few Nobel prizes in recognition of them. Following Watson and Crick’s Nobel-prize-winning seminal decipherment of the DNA-double-helix structure, there have been numerous quite mathematical works dealing with molecular sequence codes. But also there are many other aspects to this general area, concerning prebiotic evolution immunochemistry, protein chemistry, cell chemistry, and neurochemistry, as well as brain chemistry and function. Further there is intense on-going activity dealing with enzyme conformation and protein folding. (For references, see Appendix 23.)
- Chemo-informatics is an extension of ‘chemo-metrics’ (a term popularized in analytical chemistry) and is presently expanding rapidly, and is also related to the area of chemical nomenclature and related classifications. But particularly, it also encompasses topics of chemical data mining, molecular similarity comparisons, molecular pattern recognition, (virtual or theoretical) combinatorial chemistry and biomimetics, as well as of various theoretical aspects of the immense rapidly expanding related frontier areas of molecular biology, genomics, proteomics, and general bio-informatics – all deserving of a separate extensive discussion. (For references, see Appendix 24.)
- Chemical graph theory has come to be so identified over the last few decades, and significantly overlaps with polymer statistics, stereochemistry, semi-empirical quantum-chemistry, nanotechnology, structure generation, chemo-metrics/QSAR, and chemo-informatics, all already mentioned. But there are numerous other works, e.g., just in the particular area of fullerenes (yet again involving a Nobel prize, to Kroto, Smalley, and Curl) including: combinatoric methodology to apply the conjugated-circuits scheme (Herndon 1974, Randić 1977a,b); Manolopolous & Fowler’s (1992) important development of ‘topological coordinates’ for a simple geometric realization of fullerene structures; Brinkmann’s powerful methodology for generating fullerenes (and related structures) (Brinkmann & Dress 1997, 1998, Brinkmann & Greinas 2003, Brinkmann et al. 1999 in Appendix 17); characterizations of fullerene transformations (Brinkmann & Fowler 2003, Brinkmann et al. 2003); and numerous other theorematic and algorithmic fullerenic results. For a more embracing (older) overview of chemical graph theory see Trinajstić 1992 (or more briefly several earlier reviews (Trinajstić & Gutman 2002, King 2000, Balaban 2005) or an intended follow up article). (For references, focused largely just on fullerenes, see Appendix 25.)
Note that certainly there are many more examples within the frequently overlapping listed areas, likely with very important examples missing. Yet there is quite a variable degree of importance for the articles collected in the Appendix, and sometimes just secondary sources (reviews or books) are quoted – and undoubtedly biases of this reviewer are manifested. Much more could be said about mathematical results for very many of these areas – such incompleteness should not be construed as indicating exclusions of various results from mathematical chemistry, but rather as an indication of the great difficulty of making a comprehensive review. Each one of the areas are often only sparsely sampled and could be extensively expanded upon.
3. Comparisons and Qualifications
Comparison to earlier discussions may be made. Primas (1983) (over 2 decades ago) expansively described a quite abstract mathematical view of mathematical chemistry, or at least the part concerned with ‘fundamental’ quantum mechanics, which might be then taken to indicate that this is all of mathematical chemistry. Trinajstić & Gutman (2002), Balaban (2005), Gutman (2006) and King (2000) discuss mathematical chemistry with a focus on chemical graph theory, though it may be seen that the references quoted in these three articles and in the chemical-graph-theory area here are all more or less disjoint. Hauberditzl’s survey (1979) as well as March’s (1983) and Laughlin et al.’s (2000) comments again focus on quantum chemical aspects. The comments of Mackey (1997), Mallion (2005), Pauling (1987), Prelog (1987), and Karle (1987) each admittedly focus on different special areas (and seemingly do not have the intent of addressing mathematical chemistry in its fullness). Löwdin (1990) illustrates his ideas with very few of the areas in our listing, indicating just two areas, quantum chemistry and chemical graph theory, though this first area is likely intended to include our ‘ab initio quantum chemistry’, ‘semiempirical quantum chemistry’, and ‘solid-state chemistry’. Balaban (2005), Rouvray (1987), Löwdin (1990), King (2000), and Klein (1986), perhaps along with Primas (1983), all define mathematical chemistry formally similarly as we have. Yet further seemingly even D’Arcy Thompson (1918) indicates much the same definition (in his visionary ‘Growth and Form’ where he goes on to focus on his view for mathematical biology). Rouvray (1987) makes no attempt at examples, while perhaps the best attempt to indicate the great broadness is but a brief letter (1986), with only very few examples. As an overall indication of mathematical chemistry the present listing is comparatively very comprehensive and complete. The various works identified in the listings here are generally arguably mathematical.[1]
The present overall view to be taken from the listing here given is that mathematical chemistry is incredibly overwhelming. Some of the indicated areas historically derive more from physics than others, and in some of these areas significant work by physicists has then been referenced in the listing here, though all the listed applications are arguably ‘chemical’ – applying to chemical systems. Most of the researchers indicated in the listings here are primarily identified as chemists, though some (e.g., Gibbs, Hückel, Jahn, Teller, deGennes, and Wigner) are often identified as physicists, some (Debye, Prigogine, and Fisher) are often identified both as chemists and as physicists, while others (Hauptmann, Pólya, Kerber, Brinkmann, and F. Zhang) are identified as mathematicians, and a few (e.g., MacKay, Shubnikov, and Belov) are perhaps best described as crystallographers (whose field has a long independent tradition between chemistry, physics, and mineralogy). Some (like K. Ruedenberg or M. Randić) are commonly identified to a field (chemistry in these cases) other than that of their doctoral degree. There is no fundamental reason why mathematical chemistry cannot be done by scientists other than those trained exclusively as chemists. The type of mathematics used can be varied, and even the use of physics should be allowed – indeed even encouraged, as this extends and deepens the results, and interconnects the fields (chemistry and physics). But all such work dealing with (novel) mathematically formalized descriptions of chemical systems is properly part of ‘mathematical chemistry’, which then reflects the awesome richness and complexity of chemistry itself.
Thus the present view differs notably from earlier announced views of mathematical chemistry, questions remain as to its relation to more traditional areas of chemistry – such as theoretical chemistry, computer chemistry, or physical chemistry.
4. Where Does Mathematical Chemistry Fit?
Though mathematical chemistry is seemingly widespread with a long history, it is also evident that there must be intimate relations to ‘theoretical chemistry’ and ‘computer chemistry’. Particularly, the distinction between mathematical, theoretical, and computational chemistry might be deemed a delicate matter. But (in common with typical usages in physics and biology) one may look upon these distinctions as involving the three-way interplay of:
- the degree of adherence to mathematical formalism (say with explicit theorems and proofs in mathematical chemistry);
- the use of ‘scientific induction’ in theoretical chemistry, with the associated immediacy of general chemical predictions;
- the extent of usage of the computer.
Especially Coulson in 1960, but also later Primas (1983), Löwdin (1990), Roberts (1996), and King (2000) emphasized the distinction of ‘mathematical chemistry’ from ‘computational chemistry’. Perhaps Coulson’s (1960) description is clearest and most dramatic, with ‘computational chemistry’ being (in some sense) ascribed as somewhat like experimental chemistry – just involving seemingly ever more complicated computer ‘experiments’, with the ‘experimental apparatus’ being the computer.[2] That is, an experiment often seeks to test a theory with there often being much effort using extensive apparatus to draw forth the numerical data – while also computational chemistry makes much the same effort with extensive apparatus (namely the computer, and associated software) to draw forth data – and neither the experimentalist nor the computer chemist need understand the underlying theory or mathematics. As a related incidental point, the leaving of H.C. Longuet-Higgins and J.S. Griffith from theoretical (or mathematical) chemistry is said to have been born of their aversion to an ever more dominating view that theoretical chemistry was to evolve to naught but computational chemistry (March 2002). One point of some possible confusion concerns the development of novel computer algorithms[3] (Metropolis et al. 1953), which proceed by way of (mathematical) derivation (though their use is by way of computation), so that the derivation is properly part of mathematical chemistry. Again once the algorithm is in hand, there remains a problem of programming it, and at a yet later stage running it in production runs, with this last stage having evolved out of what is here argued to be mathematical chemistry. In further support of the view of computational chemistry’s experimental aspects, Coulson (1960) (as well as John Roberts (1996)) emphasized that after a ‘computer experiment’ which has generated great tabulations of numbers, there typically still remains a need of theoretical (perhaps mathematically refined) interpretation and understanding. Presumably now with ever more voluminous computer data to interpret, there is a consequent ever increasing need of theory (and mathematics) – there surely being a useful mathematics concerning ‘data mining’. Overall in its developmental stage it is deeply mathematical, while in ‘production runs’ a program’s use is more like that of an instrument in an experimental lab. Moreover, the data so generated only adds to the need for theoretical and mathematical chemistry.
The question as to the distinction between ‘mathematical chemistry’ and ‘theoretical chemistry’ is delicate, with a large degree of overlap. In fact perhaps even half the articles noted in the preceding listings of different mathematical chemistry areas may be reasonably argued to belong more to theoretical chemistry than mathematical chemistry – though still the quoted articles and books may be seen to have some (often strong) novel mathematical component. Again a difference with ‘computational chemistry’ is that it tends to deal more with individual cases (such as also does experimental chemistry), while ‘mathematical chemistry’ generally adheres more to ‘mathematical deduction’ (perhaps even with formal theorems and proofs) often of wide generality, while ‘theoretical chemistry’ uses more ‘scientific induction’. Here ‘mathematical deduction’ is understood to be by way of strict logic, while ‘scientific induction’ is by way of analogy and repeated agreements of individual predictions with experimental measurements. Of course, there are always articles which partake of more than one of these aspects – e.g., computations which are then interpreted and perhaps a novel theoretical explanation given, or theoretical articles which introduce novel mathematics but further rely on experimental interpretation or fitting to cement the relevance. For an article with different parts each closer to a different area (mathematical, theoretical, or computer chemistry), it may be proper to classify it to more than one of these areas. And some articles classifiable to one or more of these areas might also involve experimental chemistry.
That there is overlap between theoretical, mathematical, computational, and experimental chemistry should not be taken as a criticism of these distinctions. These simply correspond to different activities of which different scientists partake, and some may partake of two or more, perhaps intimately intermixed – while others may focus almost entirely on one of these aspectual activities. That is, the distinction of these aspects gives a more complete characterization of what goes on in chemistry in a quite different manner than the categorization into the various chemical divisions and fields of the preceding section. Notably this categorization of theoretical, mathematical, computational, and experimental cuts across all of science much outside of chemistry.
The relations of mathematical chemistry to the different main fields of chemistry and especially to physical chemistry and chemical physics bear further examination. But these relations have much to do with broad historical trends of development not only in chemistry, but also in physics and in mathematics. This then entails extensive further discussion, all as is to be addressed in a future separate article.
It seems that some of the previous articles on mathematical chemistry have sought to exclude or preclude mathematics mediated by physics (or by physical chemistry). But no ‘substantive’ reason has been made for such an exclusion – the exclusions being introduced by way of definitional fiat, or more subtly by way of quoted examples of mathematical chemistry. It is certain that many of the exemplary physical-chemistry-related (or chemical-physics-related) articles noted in the preceding listing here are highly mathematical and often of a novel character, while revealing very interesting things about chemical systems (e.g., as judged in several cases by awards of Nobel prizes). That such often beautiful work comes from physical chemistry should not count against the work as being part of mathematical chemistry.
Somewhat similarly, that mathematicians do not immediately pick up on much mathematical chemistry should not necessarily discount it either. Mathematical fundamentalness can be obscured due to the chemical context and applications, so that even if something is mathematically very fundamental, it may take some time to be so recognized. As an example, note Lars Onsager’s solution (1944, in Appendix 2) of the 2-dimensional Ising model, which mathematicians seem not to have noted for some decades, till especially following work by E. Lieb (1969a,b), Yang & Yang (1966a,b), and R.H. Baxter (1969, 1970, 1972) (and by many others) combining Onsager’s work with further early ideas of H.A. Bethe (1931), where-after it was seen (e.g., Biggs 1977, Takhtadzhan & Fadeev 1979) as entailing novel fundamental mathematics. Another example is Ruch & Schönhofer’s (1970, in Appendix 14) symmetry chirality characterizations, which was later recognized by Dress (1979, in Appendix 14), Fulton & Harris (1991), and Kerber (Gugisch et al. 2000, Kerber 1999, in Appendix 19) to entail novel fundamental mathematics. Another more minor case is that of Eyring & Polanyi’s ideas (1931, in Appendix 12) about ‘navigation’ (or reaction) on complex potential-energy hyper-surfaces, as has recently been seen (Porter & Critanovic 2005) to be mathematically fundamental in a general theory of dynamical systems. Sometimes it can be just an incidental albeit challenging integral evaluation (Onsager & Samaras 1934) only much later done (Lossers 2005) in pure mathematics. Again the view here is that mathematical chemistry includes novel mathematical results for chemistry, regardless of whether the results are mediated by way of physics. It seems that often the mathematical novelty is recognized in mathematics only after some individual recognized mathematician makes a point of this, so that without such a stimulus, the recognition in mathematics might even take much longer.
A mirror attitude to that of excluding physical-chemical mathematical articles is that mathematical and theoretical chemistry are entirely subsumed within physical chemistry (and chemical physics). And though one finds physical chemists or chemical physicists that seem to think this, this attitude is comparably inappropriate. That is, there is no reason to imagine that novel mathematical (and again often beautiful) work from other subdivisions of chemistry should not be counted as theoretical or mathematical. Indeed the example (of the preceding paragraph) concerning Ruch and Schönhofer’s work (1970, in Appendix 14) can be argued to come more from organic (or general) chemistry than from physical chemistry. Moreover many of the ideas identified in the listing of different mathematical chemistry areas are not generally viewed as part of physical chemistry. As a related point it is here suggested that the disguise of the field of mathematical chemistry has been fed by the (misguided) attitude that mathematical chemistry is subsumed within physical chemistry and chemical physics. This is taken up in a follow-up article – especially as regards chemical graph theory.
Though the broadness of mathematical chemistry should be clear from our detailed listings of areas, this broadness of view is in (often sharp) contrast to most of the earlier mentioned reviews of mathematical chemistry (Rouvray 1987, Löwdin 1990, Mackey 1997, Mallion 2005, Trinajstic & Gutman 2002, King 2000, Haberditzl 1979, Balaban 2005, Pauling 1987, Prelog 1987, Karle 1987, Primas 1983, March 1983), which end up often making a tight focus on the areas which are to comprise mathematical chemistry. Again mathematical chemistry is seen to overlap with all the traditional fields of chemistry.
5. Conclusion
To answer the question in the title, it is concluded that mathematical chemistry certainly ‘is’, which is to say that ‘it exists’, and moreover that it properly is an extremely broad field, with even a long and incredibly rich history of over a century of developments. Here it is argued that often many of the older mathematical developments are elsewhere categorized in other manners, so that often the field has been somewhat disguised. A substantial part of mathematical chemistry has been embedded in physical chemistry (where the connection to physics rather than mathematics has been emphasized), and other substantial portions of mathematical chemistry have been embedded in chemical structure, notation, and concepts – where often the non-numerical and non-geometrical nature of the relevant mathematics has led many to view such ideas as non-mathematical. Again, the present grand view has notable difference in comprehensiveness as compared to several previous presumably general commentaries (Rouvray 1987, King 2000, Haberditzl 1979, Balaban 2005),[4] while the present definition of ‘mathematical chemistry’ is quite similar to other earlier commentaries (Rouvray 1987, Löwdin 1990, Thompson 1918),[4] which however provide very much less overall detail than with the documentation presently marshalled here. Mathematical chemistry is seen to contact all ‘classical’ chemical fields: inorganic, organic, analytical, biochemical, and physical. Evidently some areas of mathematical chemistry have much contact with chemical physics, physics, mathematical physics, or even with biology or mathematical biology. At the same time computational chemistry has here and elsewhere (Mackey 1997, Haberditzl 1979, Coulson 1960) been distinguished from mathematical and theoretical chemistry.
Some historical questions remain to be clarified, e.g., as to why it has taken so long to make an explicit recognition of the field of mathematical chemistry. This and other questions relating to the manner of its development and to the areas of mathematics naturally distinctively close to classical chemical structure theory (such as graph theory) are to be addressed in a second article, building from the presently established broad view. As a plausible conclusion, one could argue that university curricula include mathematical chemistry – say as indicated in the Figure 1.
The curriculum could plausibly encompass computer chemistry as part of mathematical chemistry – most especially the part involving program development.
Especially mathematical and theoretical chemistry reflect the overall richness and complexity of chemistry itself. Evidently the general philosophical aim in science in making precise and unambiguous statements (of fact, of theory, or of prediction) is to implement a mathematical framework. Indeed this is somewhat a tautology – if one grants that mathematics is the realm of precision and clarity of statement (with numerics being just one form in which to so cast such statements). Notably this view of science is in complete concert with Leonardo da Vinci’s statement (White 2001): "No human investigation can be called true science which has not passed through mathematical demonstrations". And also note Galileo’s statement (1623): "The great book of nature is written in the mathematical language, ... without whose help it is impossible to comprehend a single word of it". And in a similar vein Immanuel Kant wrote (1900-2000, vol. 4, p. 470): "I believe that one may ascribe to every study of nature only so much scientific character as it contains mathematics".
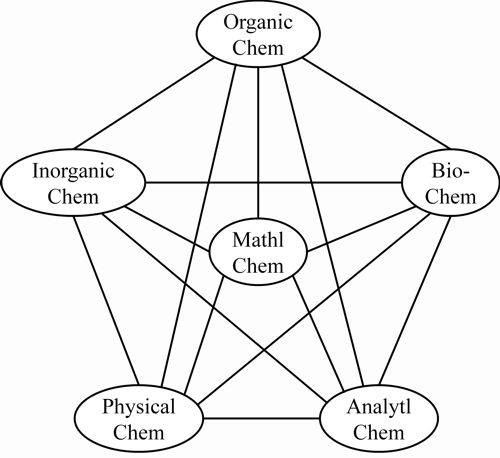
Figure 1: Inclusion of mathematical chemistry in university curricula
Thence it is emphasized that mathematics is an integral part of fundamental science in general, and chemistry in particular, so that a subdiscipline such as mathematical chemistry[5] is naturally anticipated – or perhaps even demanded. Reflecting chemistry as a whole, it is not surprising that the field is rich and diverse. Mathematical and theoretical chemistry are seen to be at the foundation of the science of chemistry. Indeed, as indicated in our discussion of the appearance of mathematical chemistry in different chemical fields, the general relevance of mathematical chemistry is well recognized in terms of the numerous examples of associated Nobel prizes awarded.
Acknowledgement
Acknowledgement is made of support (through grant BD-0894) from the Welch Foundation of Houston, Texas.
Notes
[1] Sometimes it seems likely that some of the quoted articles might be argued to be non-mathematical. Some such further discussion of just what is ‘mathematical’ is taken up in a synoptic history, where for example, there is discussion of an early article of Crum Brown (1864) on chemical notation, which many at the time considered fundamental chemistry but not mathematical, whereas we argue that it is mathematical – just not numerical. Of the quoted articles in the present exemplar section, articles which many might consider not so mathematical include those concerning acids and bases (Brønsted 1923, Lewis 1923, 1938, Usanovich 1939 in Appendix 21), which nevertheless here are argued to manifest a fundamental mathematical germ. Lewis (1938, p. 302, in Appendix 21) enunciates his ideas in terms of four formal definitional (arguably axiomatic) conditions. He allows the idea of degree of acidity, but notes (on page 299) "how impossible it is to arrange our acids in any single monotonic order", so that one perceives an indication of a ‘partial ordering’, such as is elaborated in a more formally mathematical framework (Klein 1995, Klein & Babic 1997, in Appendix 21). Overall, if something of a concrete or substantive nature has been enunciated, then it should be susceptible to mathematical formalization. Or perhaps the converse statement is better to make, that if it is not susceptible to mathematical formalization, then it is not really substantive. Perhaps it would be appropriate to leave a few of the articles out of the listing of mathematical articles, though the position taken here is that the foundational work which is being formalized has some element of the mathematical content. Another area which many might question as mathematical concerns ‘classification’ (e.g., as complicit in the mentioned chemical nomenclature). But classification is fundamentally mathematical, if made precise – this often entailing not only equivalence classes, but also various hierarchical orderings of these classes. Such matters are neatly (and often deeply) considered in isomer classification (as in Mislow 1977, in Appendix 14), substance classification, and nomenclature.
[2] In addition to computer chemistry having similarities to experiment, there are sharp differences. In computational chemistry the ‘real world’ of chemistry is substituted by a ‘virtual computer world’ controlled by the theoretical model employed. Still in either case the ‘studied world’ is itself so complex that it is often studied by a rather explicitly trial and error method, e.g., perhaps involving Monte Carlo sampling. Often significant guidance from theory is non-trivially employed, though this may be done in the usual experimental context also. Indeed techniques for guidance in one field (computer chemistry or experimental chemistry) might often be profitably transferred to the other field.
[3] A nice example here is the development of the Metropolis Monte-Carlo algorithm (Metropolis et al. 1953) for sampling state ‘configurations’ to appear in a statistical-mechanical partition function (and then entering into different statistical mechanical expectations). In fact there are numerous other examples involving derivations of ‘unbiased’ Monte-Carlo sampling techniques, e.g., Wall’s ‘slithering snake’ algorithm (Wall & Mandel 1975, in Appendix 15), or various constrained-diffusion algorithms for quantum Monte-Carlo electronic structure (Reynolds et al. 1982, Ceperley 1991; ten Haaf et al. 1995, in Appendix 9).
[4] King (2000) seems to imagine a wide range to mathematical chemistry when in passing he ascribes the development of quantum mechanics in the early 20th century as a development in mathematical chemistry. In the current article here a less extreme, more pragmatic (more conventional) view is taken: when both experiment and theory are done primarily by physicists (i.e., scientists in physics departments) who think that they are doing physics, this is identified as physics. Ambiguities remain (e.g., with thermodynamics or statistical mechanics), but so it is. Returning to King’s review, once past the comment about quantum mechanics, it is quite lop-sided in an opposite way, in illustrating mathematical chemistry such that there is essentially no mention of most of the areas detailed in the present article. Perhaps 90% of his discussion is drawn from ‘chemical graph theory’, and then almost all from within a special sub-area of this – without clearly indicating this narrow focus.
[5] Again it is noted that there is some qualification in that it is demanded that mathematical chemistry involve novel mathematics. The general argument expounded for the development of science demands only that mathematics be part of (substantive) science, without the demand that the mathematics be novel. But granted mathematics appearance in science, it seems that extensive scientific development should ultimately lead to some novel mathematics arising at some point along the way. Again in chemistry much of the more evident less trivial mathematics has often been perceived to be filtered through physics, though in principle this is something that is independent of the novelty. In some of our examples the mathematics might be argued not to be so novel – but here we let our idea of ‘novelty’ be colored by its chemical application. For instance, in the discussion of physical organic theory, various ‘linear free-energy relationships’ were identified as mathematical chemistry (thence with some novelty), though this mainly involves expressing logarithms of quantities (equilibrium constants or rate constants) as a linear combination of structural characteristics. What is novel in this case is not so much the logarithms or linear combinations, but rather the manner in which the (graph-theoretic) structural features are treated. That is, though the ‘intrinsic’ mathematics might not be novel, the area or manner of its application might be novel – perhaps so much so that some fundamental mathematics is reinvented (in a new context). Indeed such a phenomenon may be seen to occur even within mathematics proper, and an even standard sort of modus operandi in mathematics is to borrow (or more colloquially ‘steal’) from one area to build in another.
References
Balaban, A.T.: 2005, ‘Reflections on mathematical chemistry’, Foundations of Chemistry, 7, 289-306.
Baxter, R.J.:1969, ‘F model on a triangular lattice’, Journal of Mathematical Physics, 10, 1211-6.
Baxter, R.J.:1970, ‘Three colorings of the square model’, Journal of Mathematical Physics, 11, 3116-24.
Baxter, R.J.:1972. ‘Partition function of the eight-vertex lattice model’, Annals of Physics, 70, 193-228.
Bethe, H.A.: 1931, ‘Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen Atomkette’, Zeitschrift für Physik, 71, 205-26.
Biggs, N.L.: 1977, Interaction models, Cambridge: Cambridge University Press, pp. 5-9.
Coulson, C.A.: 1960, ‘Present state of molecular structure calculations’, Review of Modern Physics, 52, 170-7.
Fulton, W. & Harris, J.: 1991, Representation theory, Berlin: Springer, pp. 1-566.
Galilei, G.: 1623, Il saggiatori. Appresso G. Mascardi, Roma. English translation in Galilei, G.: 1957, The assayer. In: Galilei, G. Discoveries and opinions of Galileo, New York: Doubleday & Company, pp. 1-320.
Gutman, I.: 2006, ‘Chemical Graph Theory – The Mathematical Connection’, Advances in Quantum Chemistry, 51, 125-138.
Haberditzl, W.: 1979, ‘100 Jahre ‘Mathematische Chemie’ und 50 Jahre Theorie der Chemischen Bindung: Versuch einer Bilanz’, MATCH Communications in Mathematical and in Computer Chemistry, 7, 197-215.
Harary, F. & Palmer, E.G.:1973, Graphical enumeration, New York: Academic Press, p. 236.
Kant, I.: 1900-2000, Akademieausgabe von Immanuel Kants Gesammelten Werken, vol. 4, p. 470 [online available at http://www.korpora.org/kant/verzeichnisse-gesamt.html, accessed 20 June 2012].
Karle, J.: 1987, ‘Welcoming letter’, Journal of Mathematical Chemistry, 1, v-vii.
King, R.B.: 2000, ‘The role of mathematics in the experimental/theoretical/ computational trichotomy of chemistry’, Foundations of Chemistry, 2, 221-36.
Laughlin, R.B.; Pines, D.; Schmalian, J.; Stojković, B. P. & Wolynes, P.: 2000, ‘The middle way’, Proceedings of the National Academy of Sciences, 97, 32-7.
Lieb, E.H.:1969a, ‘Residual entropy of square ice’, Physical Review, 162, 162-71.
Lieb, E.H.:1969b, ‘Two-dimensional ice and ferroelectric models’, in: K.T. Mahantappa & W.E. Brittin (eds.), Lectues in Theoretical Physics, volume XI, New York: Gordon and Breach, pp. 329-54.
Lossers, O.P.: 2005, ‘Integral by Mellin transform’, The American Mathematical Monthly, 112, 843-4.
Löwdin, P-O.: 1990, ‘Mathematics in chemistry and in mathematical chemistry’, Journal of Mathematical Chemistry, 4, 3-14.
Mackey, A.: 1997, ‘Lucretius on the philosophy of chemistry’, Colloids and Surfaces A: Physicochemical and Engineering Aspects, 129/130, 305-10.
Mallion, R.B.: 2005, ‘An autobiographical account of chemical graph theory in the years surrounding the launch of MATCH: an Oxford participant’s highly personal and parochial reminiscence about the period 1969-1976’, MATCH Communications in Mathematical and in Computer Chemistry, 53, 15-52.
March, N.H.: 1983, ‘‘Quantum mechanics has accounted for a large part of physics and the whole of chemistry’. true or false?’, Contemporary Physics, 24, 373-87.
March, N.H.: 2002, Private communication.
Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. & Teller, E.: 1953, ‘Equations of state calculations by fast computing machines’, Journal of Chemical Physics, 21, 1087-92.
Onsager, L. & Samaras, N.N.T.: 1934, ‘The surface tension of Debye-Huckel electrolytes’, Journal of Chemical Physics, 2, 528-36.
Pauling, L.: 1987, ‘Welcoming letter’, Journal of Mathematical Chemistry, 1, v-vii.
Porter, M. & Critanovic, P.: 2005, ‘Ground control to Niels Bohr: Exploring outer space with atomic physics’, Notices of the American Mathematical Society, 52, 1020-5.
Prelog, V.: 1987, ‘Welcoming letter’, Journal of Mathematical Chemistry, 1, v-vii.
Primas, H.: 1983, Chemistry, quantum mechanics and reductionism, Berlin: Springer, pp. 1-441.
Roberts, J.D.: 1996, ‘The beginnings of physical organic chemistry in the US’, Bulletin for the History of Chemistry, 19, 48-56.
Rouvray, D.H.: 1987, ‘Editorial foreword’, Journal of Mathematical Chemistry, 1, i-iv.
Takhtadzhan, L.A. & Fadeev, L.D.: 1979, Russian Mathematical Surveys, 34, 11-68.
Thompson, D.W.: 1918, On growth and form, Cambridge: Cambridge University Press, pp. 1-14.
Trinajstić, N. & Gutman I.: 2002, ‘Mathematical chemistry’, Croatica Chemica Acta, 75, 329-56.
White, M.: 2001, Leonardo: the first scientist, London: Abacus Press, p. 153.
Yang, C.N. & Yang, C.P.: 1966a, ‘One-dimensional chain of anisotropic spin-spin interactions. I. Proof of Bethe’s hypothesis for ground state in a finite system’, Physical Review, 150, 321-7.
Yang, C.N. & Yang, C.P.: 1966b, ‘One-dimensional chain of anisotropic spin-spin interactions. II. Properties of the ground-state energy per lattice site for an infinite system’, Physical Review, 150, 327-39.
Appendix: Thematic Bibliography
1. Foundational equilibrium thermodynamics
Arrhenius, S.: 1913, Theories of solutions, New Haven: Yale University Press, pp. 1-72.
Fisher, M.E.: 1972, Proceedings of the 1970 Enrico Fermi summer school, Corso LI, New York: Academic Press, p. 41.
Gibbs, J. W.: 1928, Collected works. Volume I. Thermodynamics, New York: Longman Greens.
Guggenheim, E.A.: 1945, ‘The principle of corresponding states’, The Journal of Chemical Physics, 13, 253-61.
Haber, F.: 1905, Thermodynamik technischer Gasreaktionen, Munich: Oldenbourg, pp. 1-296.
Hill, T.L.: 1964, Thermodynamics of small systems, New York: Benjamin W. A., p. 1-210.
Kepler, J.: 1908, Ostwalds’s Klassiker der exakten Wissenschaften, Leipzig: Engelmann, pp. 1-130.
Lewis, G.N. & Randall, M.: 1961, Thermodynamics, New York: McGraw-Hill, pp. 1-723.
Nernst, W.: 1907, Experimental and theoretical applications of thermodynamics to chemistry, New York: Charles Scribner’s Sons, pp. 1-123.
Ostwald, W.: 1890, Outlines of general chemistry, London: MacMillan & Co., pp. 1-372.
Pitzer, K.S.: 1939, ‘Corresponding states for perfect liquids’, The Journal of Chemical Physics, 7, 583-90.
Ruskai, M.R. & Stillinger, F.H: 1990, ‘Convexity inequalities for estimating free energy and relative entropy’, Journal of Physics A: Mathematical and General, 23, 2421-37.
Weinhold, F.: 1975a, ‘Metric geometry of equilibrium thermodynamics’, The Journal of Chemical Physics, 63, 2479-83.
Weinhold, F.: 1975b, ‘Metric geometry of equilibrium thermodynamics. II. Scaling, homogeneity, and generalized Gibbs–Duhem relations’, The Journal of Chemical Physics, 63, 2484-7.
Weinhold, F.: 1975c, ‘Metric geometry of equilibrium thermodynamics. III. Elementary formal structure of a vector-algebraic representation of equilibrium thermodynamics’, The Journal of Chemical Physics, 63, 2488-95.
Weinhold, F.: 1975d, ‘Metric geometry of equilibrium thermodynamics. IV. Vector-algebraic evaluation of thermodynamic derivatives’, The Journal of Chemical Physics, 63, 2496-501.
Widom, B.: 1965, ‘Surface tension and molecular correlations near the critical point’, The Journal of Chemical Physics, 43, 3892-905.
Widom, B.: 1974, ‘Critical point and scaling theory’, Physica, 73, 107-18.
2. Equilibrium statistical mechanics
Belkasri, A.K. & Huckaby, D.: 1997, ‘Presence of racemic phases at low temperatures in a three-dimensional lattice gas of enantiomers’, Journal of Physics A: Mathematical and Theoretical, 30, 6205-14.
Bethe, H.A. & Kirkwood, J.G.: 1939, ‘Critical behavior of solid solutions in the order-disorder transformation’, The Journal of Chemical Physics, 7, 578-82.
Bogoliubov, N.N.: 1962, Studies in statistical mechanics, Amsterdam: North-Holland, p. 5.
Chandler, D.: 1987, Introduction to Modern Statistical Mechanics, Oxford: Clarendon Press, p. 1-274.
Essam, J.W. & Fisher, M.E.: 1963, ‘Pade approximant studies of the lattice gas and Ising ferromagnet below the critical point’, The Journal of Chemical Physics, 38, 802-12.
Fisher, M.E. & Szpilka, A.M.: 1987a, ‘Domain-wall interactions. I’, Physical Review B, 36, 644-6.
Fisher, M.E. & Szpilka, A.M.: 1987b, ‘Domain-wall interactions. II’, Physical Review B, 36, 5343-62.
Fisher, M.E. & Szpilka, A.M.: 1987c, ‘Domain-wall interactions. III’, Physical Review B, 36, 5363-76.
Green, M.S.: 1956, ‘Boltzmann equation from the statistical mechanical point of view’, The Journal of Chemical Physics, 25, 836-55.
Kauffmann, B. & Onsager, L.: 1949a, ‘Crystal statistics. II’, Physical Review, 76, 1232-43.
Kauffmann, B. & Onsager, L.: 1949b, ‘Crystal statistics. III’, Physical Review, 76, 1244-52.
Kirkwood, J.G.: 1940, ‘Statistical mechanics of cooperative phenomena’, The Journal of Chemical Physics, 8, 623-7.
Mayer, J. & Harrison, S.F.: 1938a, ‘Statistical mechanics of condensing systems. III’, The Journal of Chemical Physics, 6, 87-100.
Mayer, J. & Harrison, S.F.: 1938b, ‘Statistical mechanics of condensing systems. IV’, The Journal of Chemical Physics, 6, 101-4.
Montroll, E.P. & Mayer, J.E.: 1941a, ‘Theory of imperfect gases’ The Journal of Chemical Physics, 9, 626-37.
Montroll, E.P.: 1941b, ‘Statistical mechanics of nearest neighbor systems’, The Journal of Chemical Physics, 9, 706-21.
Onsager, L.: 1944, ‘Crystal statistics I. A two-dimensional model with an order-disorder transition’, Physical Review, 65, 117-49.
Rice, S. A. & Gray, P.: 1965, Statistical mechanics of simple liquids, New York: Interscience Pub., p. 1-582.
Riddell, R.J. & Uhlenbeck, G.E.: 1953, ‘On the theory of the virial development of the equation of state of monoatomic gases’, The Journal of Chemical Physics, 21, 2056-64.
Shinmi, M. & Huckaby, D.: 1989, ‘A lattice gas model for neopentane’, Bulletin of the Chemical Society of Japan, 62, 1376-8.
3. Electrochemistry
Aviram, A. & Ratner, M.A.: 1974, ‘Molecular rectifiers’, Chemical Physics Letters, 29, 277-83.
Bixon, M. & Jortner, J.: 1997, ‘Electron transfer via bridges’, The Journal of Chemical Physics, 107, 5154-70.
Buck, R.P.: 1988, ‘Electron hopping in one dimension: Mixed conductor membranes’, The Journal of Physical Chemistry, 92, 4196-200.
Chandra, A. & Bagchi, B.: 2000, ‘Beyond the classical transport laws of electrochemistry: A new microscopic approach to ionic conductance & viscosity’, The Journal of Physical Chemistry B, 104, 9067-80.
Coronado, E. & Day, P.: 2004, ‘Magnetic molecular conductors’, Chemical Reviews, 104, 5419-48.
Davis, W.B.; Ratner, M.A. & Wasielewski, M.R.: 2001, ‘Conformational gating of Log distance electron transfer through wire-like bridges in donor-bridge-acceptor molecules’, Journal of the American Chemical Society, 123, 7877-86.
Debye, P.W. & Hückel, E.: 1923a, ‘The theory of electrolytes. I. Lowering of freezing point and related phenomena’, Physikalische Zeitschrift, 24, 185-206.
Debye, P.W. & Hückel, E.: 1923b, ‘The theory of electrolytes. II. The limiting law of electrical conductivity’, Physikalische Zeitschrift, 24, 305-25.
Forland, K.S. & Forland, T.: 1995, ‘An alternative approach to electrochemistry’, Journal of Statistical Physics, 78, 513-29.
Fuoss, R.M. & Onsager, L.: 1957, ‘Conductance of unassociated electrolytes’, The Journal of Physical Chemistry, 61, 668-82.
Goychuk, I & Hanggi, P.: 2001, ‘Minimal quantum rectifiers’, The Journal of Physical Chemistry B, 105, 6642-7.
Grahame, D.C.: 1947, ‘The electrical double layer and the theory of electrocapillarity’, Chemical reviews, 41, 441-501.
Haberkorn, R.; Michel-Beyerle, M.E. & Marcus, R.A.: 1979, ‘On spin-exchange and electron-transfer rates in bacterial photosynthesis’, Proceedings of the National Academy of Sciences of the United Satates of America, 76, 4185-8.
Ise, N. & Okubo, T.: 1980, ‘‘Ordered’ distribution of electrically charged solutes in dilute solutions’, Accounts of Chemical Research, 13, 303-9.
Kemp, M.; Mujica, V. & Ratner, M.A.: 1994, ‘Molecular electronics: Disordered molecular wires’, The Journal of Chemical Physics, 101, 5172-8.
Kestner, N.R.: 1980, ‘Theory of electron transfer reactions of solvated electrons’, The Journal of Physical Chemistry, 84, 1270-5.
Kolb, D.M.: 2002, ‘An atomistic view of electrochemistry’, Surface Science, 500, 722-40.
Lustenberger, P.; Rohrer, H.; Christoph, R. & Siegenthaler, H.: 1988, ‘Scanning tunneling microscopy at potential-controlled electrode surfaces in electrolytic environment’, Journal of Electroanalytical Chemistry, 243, 225-35.
Marcus, R.A.: 1956, ‘The theory of oxidation-reduction reactions involving electron transfer. I’, The Journal of Chemical Physics, 24, 966-78.
Marcus, R.A.: 1965, ‘Theory of electron-transfer reactions. VI. Unified treatment for homogeneous and electrode reactions’, The Journal of Chemical Physics, 43, 679-701.
Marcus, R.A.: 1977, On the theory of overvoltage for electrode processes possessing electron transfer mechanisms. I., Amsterdam: Elsevier, p. 180-209.
Marcus, R.A.: 1993, ‘Electron transfer reactions in chemistry. Theory and experiment’, Reviews of Modern Physics, 65, 599-610.
McIntyre, D.E. & Kolb, D.M.: 1970, ‘Specular reflection spectroscopy of electrode surface films’, Symposia of the Faraday Society, 4, 99-113.
Pitzer, K.S.: 1973, ‘Thermodynamics of electrolytes. I. Theoretical basis and general equations’, The Journal of Physical Chemistry, 77, 268-77.
Pitzer, K.S. & Mayorga, G.: 1973, ‘Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent’, The Journal of Physical Chemistry, 77, 2300-8.
Pitzer, K.S. & Kim, J.J.: 1974, ‘Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes’, Journal of the American Chemical Society, 96, 5701-7.
Pitzer, K.S.: 1995, ‘Ionic fluids: Near-critical and related properties’, The Journal of Physical Chemistry, 99, 13070-7.
Ratner, M.A. & Madhukar, A.: 1978, ‘On the role of nuclear motions in electron and excitation transfer rates: Importance of transfer-integral dependence upon nuclear coordinate’, Chemical Physics, 30, 201-15.
Schlag, E.W.; Yang, D.-Y.; Sheu, S.-Y.; Selzle, H.L.; Lin, S.H. & Rentzepis, P.M.: 2000, ‘Dynamical principles in biological processes: A model of charge migration in proteins & DNA’, Proceedings of the National Academy of Sciences of the United States of America, 97, 9849-54.
Skourtis, S.S. & Beratan, D.N.: 1997, ‘Electron transfer contact maps’, The Journal of Physical Chemistry B, 101, 1215-34.
Stuchebrukhov, A.A.: 1996, ‘Tunneling currents in electron transfer reaction in proteins’, The Journal of Chemical Physics, 104, 8424-32.
Sumi, H. & Kakitani, T.: 2001, ‘Unified theory on rates for electron transfer mediated by a midway molecule, bridging between superexchange and sequential processes’, The Journal of Physical Chemistry B, 15, 9603-22.
4. Chemical kinetics
Clark, B.: 1975, ‘Stability of topologically similar networks’, The Journal of Chemical Physics, 62, 3726-38.
Eigen, M.: 1971, ‘Self-organization of matter and the evolution of biological macromolecules’, Naturwissenschaften, 58, 465-523.
Eigen, M. & Schuster, P.: 1977, ‘The hypercycle. A principle of natural self-organization. Part A: Emergence of the hypercycle’, Naturwissenschaften, 64, 541-65.
Eigen, M. & Schuster, P.: 1978, ‘The hypercycle. A principle of natural self-organization. Part C. The realistic hypercycle’, Naturwissenschaften, 65, 341-69.
Field, R.J. & Noyes, R.M.: 1974, ‘Oscillations in chemical systems. V. Quantitative explanation of band migration in the Belousov-Zhabotinskii reaction’, Journal of the American Chemical Society, 96, 2001-6.
Gray, B.F. & Aarons, L.J.: 1974, ‘Small parasitic parameters and chemical oscillations’, Faraday Symposia of the Chemical Society, 9, 129-36.
Hill, T.L.: 1977, Free energy transduction in biology, New York: Academic Press, p. 1-229.
Lefever, R.; Nicolis, G. & Prigogine, I.: 1967, ‘On the occurrence of oscillations around the steady state in systems of chemical reactions far from equilibrium’, The Journal of Chemical Physics, 47, 1045-6.
Lefever, R.; Nicolis, G. & Prigogine, I.: 1968, ‘On the occurrence of oscillations around the steady state in systems of chemical reactions far from equilibrium’, The Journal of Chemical Physics, 48, 1045-8.
Noyes, R.M.; Field, R. & Koros, E.: 1972a, ‘Oscillations in chemical systems. I. Detailed mechanism in a system showing temporal oscillations’, Journal of the American Chemical Society, 94, 1394-5.
Noyes, R.M.; Field, R. & Koros, E.: 1972b, ‘Oscillations in chemical systems. II. Thorough analysis of temporal oscillation in the bromate-cerium-malonic acid system’, Journal of the American Chemical Society, 94, 8649-64.
Noyes, R.M. & Field, R.J.: 1974, ‘Oscillatory chemical reactions’, Annual Review of Physical Chemistry, 25, 95-119.
Oster, G.F. & Auslander, D.M.: 1971a, ‘Topological representations of thermodynamic systems – I. Basic concepts’, Journal of the Franklin Institute, 292, 1-17.
Oster, G.F. & Auslander, D.M.: 1971b, ‘Topological representations of thermodynamic systems – II. Some elemental subunits for irreversible thermodynamics’, Journal of the Franklin Institute, 292, 77-92.
Peusner, L.: 1986, Studies in network thermodynamics, Amsterdam: Elsevier, p. 1-369.
Prigogine, I. & Lefever, R.: 1968, ‘Symmetry breaking instabilities in dissipative systems. II’, The Journal of Chemical Physics, 48, 1695-700.
Rice, S.A.; Toda, M.; Komatsuzaki, T.; Konishi, T. & Berry, R.S.: 2005, Geometric Structures of Phase Space in Multi-Dimensional Chaos: Applications to Chemical Reaction Dynamics in Complex Systems, Volume 130, New York: John Wiley & Sons, pp. 1-542.
Schnakenberg, J.: 1977, Thermodynamic network analysis of biological systems, Berlin: Springer, pp. 1-149.
Scott, S.K.: 1991, Chemical chaos, Oxford: Clarendon, pp. 1-451.
5. Non-equilbrium thermodynamics
Katchalsky, A. & Curran, A.P.: 1965, Nonequilibrium thermodynamics for biophyics, Cambridge: Harvard U. Press, pp. 1-248.
Keizer, J.: 1987, Statistical thermodynamics of nonequilibrium processes, Berlin: Springer, pp. 1-495.
Kirkwood, J.G. & Crawford, B.: 1952, ‘Macroscopic equations of transport’, The Journal of Physical Chemistry, 56, 1048-51.
Onsager, L.: 1931, ‘Reciprocal relations in irreversible processes. I,’ Physical Review, 37, 405-26.
Onsager, L. & Machlup, S.: 1953a, ‘Fluctuations & irreversible thermodynamics. I’, Physical Review, 91, 1505-12.
Onsager, L. & Machlup, S.: 1953b, ‘Fluctuations & irreversible thermodynamics. II’, Physical Review, 91, 1512-22.
Prigogine, I.: 1945, ‘The theorem of minimum entropy production’, Academie Royale de Belgique. Bulletin de la Classe des Sciences, 31, 600-6.
Prigogine, I.: 1967, Introduction to thermodynamics of irreversible processes, New York: Wiley-Interscience, pp.1-147.
Prigogine, I. & Henin, F.: 1969, ‘Kinetic theory and subdynamics’, Journal of the Soviet Academy of Sciences, 356-64.
Prigogine, I.; George, C.; Henin, F. & Rosenfeld, L.: 1973, ‘Unified formulation of dynamics and thermodynamics. With special reference to non-equilibrium statistical thermodynamics’, Chemica Scripta, 4, 5-32.
Ruch, E.: 1975, ‘The diagram lattice as structural principle. A. & B.’, Theoretica Chimica Acta, 8, 167-83.
Ruch, E.: 1992, ‘Der Richtungsabstand’, Acta Applicandae Mathematicae, 30, 67-93.
6. Spectroscopic theory
Abragam, A.: 1961, The principles of nuclear magnetism, Oxford: Oxford University Press, pp. 1-599.
Allen, H.C. & Cross, P.C.: 1963, Molecular vib-rotors, New York: Wiley, p. 1-324.
Carrington, A. & MacLachlan, A.D.: 1967, Introduction to magnetic resonance, New York: Harper, pp. 1-266.
Corio, P.L.: 1966, Structure of high-resolution NMR spectra, New York: Academic Press, pp. 1-548.
Davydov, A.S.: 1951, Molecular exciton theory, New York: McGraw-Hill.
Decius, J.C. & Hexter, R.M.: 1977, Molecular vibrations in crystals, New York: McGraw-Hill, p. 1-391.
Engelmann, R.: 1972, The Jahn-Teller effect in molecules and crystals, New York: Wiley-Interscience, p. 1-350.
Ernst, R.R.; Bodenhausen, G. & Wokaun, A.: 1987, Principles of nuclear magnetic resonance in one and two dimensions, New York: Oxford University Press, pp. 1-640.
Ernst, R.R.: 1992, ‘Nuclear magnetic resonance Fourier transform spectroscopy’, Angewandte Chemie International Edition, 31, 805-23.
Field, R. W.: 1988, Nonlinear spectroscopy for molecular structure determination, Massachusetts: Oxford Blackwell Science, pp. 1-276.
Griffiths, P.R. & De Haseth, J.A.: 1986, Fourier transform infrared spectroscopy, New York: Wiley, pp. 1-529.
Herzberg, G.: 1950, Electronic spectra and electronic structure of diatomic molecules, Princeton: van Nostrand.
Herzberg, G.: 1967, Electronic spectra and electronic structure of polyatomic molecules, Princenton: van Nostrand, pp. 1-741.
Herzberg, G.: 1968, Infrared and Raman spectra of polyatomic molecules, Pricenton: van Nostrand, p. 1-632.
James, T.L.; Suzuki, E.-I.; Tattabiraman, N. & Zon, G.: 1987, ‘2D NOE full relaxation matrix analysis and molecular mechanics calculations for structure determination in solution: DNA fragments’, The Bulletin of Magnetic Resonance, 8, 152-7.
Jeener, J.; Meier, B.H.; Bachmann, P. & Ernst, R.R.: 1979, ‘Investigation of exchange processes by two-dimensional NMR spectroscopy’, The Journal of Chemical Physics, 71, 4546-53.
Kroto, H.W.: 1975, Molecular rotation spectra, New York: Wiley, pp. 1-311.
Kroto, H.W.: 1992, Molecular rotation spectra, New York: Dover, pp. 1-352.
Lascombe, J. & Huong, P.V.: 1982, Raman spectroscopy linear and nonlinear, New York: Wiley, pp. 1-834.
Marshall, A. G.: 1985, ‘Fourier transform ion cyclotron resonance mass spectrometry’, Accounts of Chemical Research, 18, 316-22.
Marshall, A.G. & Verdun, F.R.: 1990, Fourier transforms in NMR, optical, and mass spectrometry: A users handbook, Amsterdam: Elsevier, pp. 1-450.
McGilp, J.; Weaire, D.L.; Patterson, C.H.: 1995, Epiotics: Linear and nonlinear optical spectroscopy of surfaces and interfaces, Berlin: Springer, pp. 1-230.
Merrifield, R.E.: 1964, ‘Theory of the vibrational structure of molecular exciton states’, The Journal of Chemical Physics, 40, 445-50.
Mertz, J.; Guntert, P.; Wuthrich, K. & Braun, W.: 1991, ‘Complete relaxation matrix refinement of NMR structures of proteins using analytically calculated dihedral angle derivatives of NOE intensities’, Journal of Biomolecular NMR, 1, 257-69.
Mukamel, S. & Abramavicius, D.: 2004, ‘Many-body approaches for simulating coherent nonlinear spectroscopies of electronic and vibrational excitons’, Chemical Reviews, 104, 2073-98.
Mukamel, S.: 1995, Principles of nonlinear optical spectroscopy, Oxford: Oxford University Press, pp. 1-543.
Perrin, C.L. & Dwyer, T.J.: 1990, ‘Application of two-dimensional NMR to kinetics of chemical exchange’, Chemical Reviews, 90, 935-67.
Pollans, W. & Choi, S.: 1970, ‘Exciton states and optical spectra in linear molecular crystals’, The Journal of Chemical Physics, 52, 3691-702.
Schmidt-Rohr, K. & Spiess, H.: 1994, Multidimensional Solid-State NMR and polymers, Amsterdam: Elsevier, p. 1-496.
Sorensen, O.W.; Eich, G.W.; Levitt, M.H.; Bodenhausen, G. & Ernst, R.R.: 1983, ‘Product operator formalism for the description of NMR pulse experiments’, Progress in Nuclear Magnetic Resonance Spectroscopy, 16, 161-92.
Villaeys, A.A. & Fujimura, Y.: 2008, Advances in multi-photon processes and spectroscopy, Singapore: World Scientific, pp. 1-304.
Wigner, E.P.: 1930, ‘Über die elastischen Eigenschwingungen symmetrischer Systeme’, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, Heft 2, 133-46.
Wigner, E.P.: 1931, Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomspektren, Braunschweig: Vieweg, pp. 1-332 (translated & reprinted as Wigner, E.P.: 1959, Group theory and its application to the quantum mechanics of atomic spectra, New York: Academic Press, pp. 1-386).
Wilson, E.B.: 1934, ‘The degeneracy, selection rules and other properties of the normal vibrations of certain polyatomic molecules’, The Journal of Chemical Physics, 2, 432-3.
Wilson, E.B.; Decius, J.C. & Cross, P.C.: 1955, Molecular vibrations: the theory of infrared and Raman vibrational spectra, New York: McGraw-Hill, p. 1-388.
Wilson, E.B. & Howard, J.B.: 1936, ‘Vibration-Rotation Energy Levels Polyatomic Molecules. I. Mathematical Theory for Semirigid Asymmetrical Top Molecules’, Journal of Chemical Physics, 4, 260-8.
7. Mathematical crystallography
De Bruijn, N.G.: 1981, ‘Algebraic theory of Penrose’s non-periodic tilings’, Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen A, 84, 39-66.
Delgado-Friedrichs, O. & O’Keeffe, M.: 2003, ‘Identification of and symmetry computation for crystal nets’, Acta Crystallographica A, 59, 351-60.
Hauptman, H. & Karle, J.: 1957a, ‘A unified algebraic approach to the phase problem. I. Space group P1’, Acta Crystallographica, 10, 267-70.
Hauptman, H. & Karle, J.: 1957b, ‘A unified algebraic approach to the phase problem. II. Space group P1’, Acta Crystallographica, 10, 515-24.
Hauptmann, H.A.: 2008, On the beauty of science, New York: Prometheus Books, pp. 1-113.
Karle, J. & Hauptman, H.: 1953, ‘Probability distribution of the magnitude of a structure factor. I. The centrosymmetric crystal’, Acta Crystallographica, 6, 131-5.
Karle, J. & Hauptman, H.: 1960, ‘A unified program for phase determination, type 3P2’, Acta Crystallographica, 13, 469-76.
Kramer, P.: 1982, ‘Non-periodic central space filling with icosahedral symmetry using copies of seven elementary cells’, Acta Crystallographica A, 38, 257-64.
Levine, D. & Steinhardt, P.J.: 1986, ‘Quasicrystals. I. Definition and structure’, Physical Review B, 34, 596-16.
Mackay, A.L.: 1975, ‘Generalised crystallography’, Isvjestaj Jugoslav. Centra Kristalografska, 10, 15-36.
Mackay, A.L.: 1982, ‘Crystallography and the Penrose pattern’, Physica A: Statistical Mechanics and its Applications, 114, 609-13.
O’Keefe, M. & Brese, N.E.: 1992, ‘Uninodal 4-connected 3D nets. I. Nest without 3 or 4-rings’, Acta Crystallographica A, 48, 663-9.
Penrose, R.: 1978, ‘Pentaplexity’, Eureka, 39, 16-22.
Robinson, R.M.: 1978, ‘Undecidable tiling problems in the hyperbolic plane’, Inventiones Mathematicae, 44, 259-64.
Shubinikov, A.V. & Belov, A.N.: 1964, Colored symmetry, New York: Macmillan, pp. 1-263.
Socloar, J.E.S. and Steinhardt, P.J.: 1986, ‘Quasicrystals. II. Unit-cell configurations’, Physical Review B, 34, 617-47.
Wells, A.F.: 1954a, ‘The geometrical basis of crystal chemistry. Part 1’, Acta Crystallographica, 7, 535-44.
Wells, A.F.: 1954b, ‘The geometrical basis of crystal chemistry. Part 2’, Acta Crystallographica, 7, 545-54.
Wells, A.F.: 1972, ‘The geometrical basis of crystal chemistry. Part 12’, Acta Crystallographica B, 28, 711-3.
8. Diffractive methods
Azároff, L.V. & Buergers, J.M.: 1958, The powder method in X-ray crystallography, New York: McGraw-Hill, p. 1-342.
Klug, H.P. & Alexander, L.: 1954, X-ray diffraction procedures for polycrystalline and amorphous materials, New York: Wiley, pp. 1-992.
Sim G.A. & Sutton, L.E.: 1973, Molecular structure by diffraction methods, London: Royal Society of Chemistry, pp. 1-824.
Sim G.A. & Sutton, L.E.: 1975, Molecular structure by diffraction methods, London: Royal Society of Chemistry, pp. 1-514.
Wormald, J.R.: 1973, Diffraction methods, Oxford: Oxford University Press, p. 1-112.
9. Ab initio quantum chemistry
Anderson, J.B.: 1976, ‘Quantum chemistry by random walk: H 2P, H3+ D3h 1A1’, H2 3Σ+u, H4 1Σ+g, Be 1S’, The Journal of Chemical Physics, 65, 4121-7.
Bartlett, R.J.; Kucharski, S.A. & Noga, J.: 1989, ‘Alternative coupled-cluster ansätze. II. The unitary coupled-cluster method’, Chemical Physics Letters, 155, 133-40.
Beste, A. & Bartlett, R.: 2002, ‘Ensuring N-representability: Coleman’s algorithm’, Chemical Physics Letters, 355, 263-9.
Born, G. & Öhrn, Y.: 1978, ‘Alternative inner projections of the superoperator resolvent’, International Journal of Quantum Chemistry, 12, 143-51.
Boys, S.F.: 1950, ‘Electronic wave functions I. A general method to calculate the stationary states of any molecular system’, Proceedings of the Royal Society A, 200, 542-54.
Ceperley, D.M.: 1991, ‘Fermion nodes’, Journal of Statistical Physics, 63, 1237-67.
Cioslowski, J.: 1987, ‘Connected-moments expansion: A new tool for quantum many-body theory’, Physical Review Letters, 58, 83-5.
Čížek, J.: 1966, ‘On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods’, The Journal of Chemical Physics, 45, 4256-65.
Čížek, J.; Paldus, J. & Sroubkova, L.: 1969, ‘Cluster expansion analysis for delocalized systems’ International Journal of Quantum Chemistry, 3, 149-67.
Čížek, J. & Paldus, J.: 1970, ‘Stability conditions for the solutions of the Hartree-Fock equations for atomic and molecular systems. III. Rules for the singlet stability of Hartree-Fock solutions of π-electronic systems’, The Journal of Chemical Physics, 53, 821-9.
Coleman, A.J.: 1963, ‘Structure of fermion density matrices’, Reviews of Modern Physics, 35, 668-86.
Coleman, A.J. & Jukalov, V.I.: 2000, Reduced density matrices: Coulson’s challenge, Berlin: Springer, pp. 1-282.
Davidson, E.R.: 1976, Reduced density matrices in quantum chemistry, New York: Academic Press, pp. 1-135.
Flocke, N. & Bartlett, R.J.: 2004, ‘A natural linear scaling coupled-cluster method’, The Journal of Chemical Physics, 121, 10935-44.
Freed, K.F. & Sheppard, M.G.: 1982, ‘Ab initio treatments of quasidegenerate many-body perturbbation theory within the effective valence shell hamiltonian formalism’, The Journal of Physical Chemistry, 86, 2130-3.
Hall, G.G.: 1951, ‘The molecular-orbital theory of chemical valency. VIII. A method of calculating ionization potentials’, Proceedings of the Royal Society A, 205, 541-52.
Hall, G.G.: 1976, ‘A new formulation of the correlation problem’, in: J-L. Calais, O. Goscinski, J. Linderberg, Y. Öhrn (eds.), Quantum science, New York: Springer Science, pp. 433-44.
Harris, F.E. & Michels, H.: 1967, ‘The evaluation of molecular integrals for Slater-type orbitals’, in: I. Prigogine (ed.), Advances in Chemical Physics, volume 13, New York: Wiley, pp. 205-66.
Hose, G. & Kaldor, U.: 1982, ‘Quasidegenerate perturbation theory’, The Journal of Physical Chemistry, 86, 2133-53.
Huzinaga, S.: 1965, ‘Gaussian-type functions for polyatomic systems’, The Journal of Chemical Physics, 42, 1293-303.
Jensen, B.R. & Linderberg, J.: 1999, ‘Propagation matrices from the finite element method’, The Journal of Physical Chemistry A, 103, 9475-8.
Klein, D.J. & Pickett, H.M.: 1976, ‘Nodal hypersurfaces and Anderson’s random-walk simulation of the Schroedinger equation’, The Journal of Chemical Physics, 64, 4811-2.
Kotani, M.; Amemiya, A.; Ishiguro, E. & Kimura, T.: 1955, Tables of molecular integrals, Tokyo: Maruzen, pp. 1-328.
Kryachko, E.S. & Ludena, E.V.: 1991, ‘Formulation of N- and v-representable density functional theory. VIII’, The Journal of Chemical Physics, 95, 9054-9.
Kutzelnigg, W.; Shamasundar, K.R. & Mukherjee, D.: 2010, ‘Spin free formulation of reduced density matrices, density cumulants, and generalized normal ordering’, Molecular Physics, 108, 433-51.
Lefebvre, R. & Moser, C.: 1969, Advances in Chemical Physics: Correlation effects in atoms and molecules, vol. 14, New York: Interscience Pub., pp. 1-546.
Löwdin, P.O.: 1955, ‘Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals and convergence problems in the method of configuration interaction’, Physical Review, 97, 1474-89.
Mishra, M.; Froelich, P. & Öhrn, Y.: 1981, ‘The dilated electron propagator: a bi-orthogonal approach’, Chemical Physics Letters, 81, 339-46.
Nakatsuji, H.: 1999, ‘Equation for the direct determination of the density matrix: Time-dependent density equation and perturbation theory’, Theoretical Chemistry Accounts, 102, 97-104.
Nooijen, M. & Bartlett, R.J.: 1997, ‘Similarity transformed equation-of-motion coupled-cluster theory: Details, examples, and comparisons’, The Journal of Chemical Physics, 107, 6812-30.
Paldus, J & Čížek, J.: 1971, ‘Stability conditions for the solutions of the Hartree-Fock equations for atomic and molecular systems. IV. Doublet stability for odd linear polyenic radicals’, The Journal of Chemical Physics, 54, 2293-303.
Poshusta, R.D. & Browne, J.C.: 1962, ‘Quantum-mechanical integrals over Gaussian atomic orbitals’, The Journal of Chemical Physics, 36, 1933-7.
Primas, H.: 1965, Separability in many-electron systems, New York: Academic Press, p. 45-74.
Redmond, L.T.; Purvis, G. & Öhrn, Y.: 1975, ‘Higher-order decoupling of the electron propagator’, The Journal of Chemical Physics, 63, 5011-7.
Reynolds, P.J.; Ceperley, D.M.; Alder, B.J. & Lester, W.A.: 1982, ‘Fixed-node quantum Monte Carlo for molecules’, The Journal of Chemical Physics, 7, 5593-603.
Roothaan, C.C.J.: 1951, ‘New developments in molecular orbital theory’, Reviews of Modern Physics, 23, 69-89.
Ruedenberg, K.: 1951, ‘Two-center integrals useful in calculations on molecular structure. II. The two-center exchange integrals’, The Journal of Chemical Physics, 19, 1459-77.
Shavitt, I.: 1963, ‘The gaussian function in calculations of statistical mechanics and quantum mechanics’, in: B. Alder; H. Feshbach & M. Rotenberg (eds.), Methods in computational physics, volume 2, New York: Academic Press, pp. 1-72.
Sheppard, M.G.; Freed, K.F.; Herman, M.F. & Yeager, D.L.: 1979, ‘Generalized perturbation theory of effective valence shell Hamiltonians’, Chemical Physics Letters, 61, 577-81.
Sinanoglu, O.: 1962, ‘Many-electron theory of atoms and molecules I. Shells, electron pairs vs. many-electron correlations’, The Journal of Chemical Physics, 36, 706-17.
Slater, J.C.: 1930, ‘Atomic shielding constants’, Physical Review, 36, 57-64.
ten Haaf, D.F.B.; van Bemmel, H.J.M.; van Leeuwen, J.M.J. & van Saarloos, W.: 1995, ‘Proof for an upper bound in fixed-node Monte Carlo for lattice fermions’, Physical Review B, 51, 13039-45.
Valdemoro, C.: 1992, ‘Approximating the second-order reduced density matrix in terms of the first order one’, Physical Review A, 45, 4462-7.
10. Density functional theory
Bader, R.F.W.: 1994, Atoms in Molecules: A quantum theory, Oxford: Oxford University Press, pp. 1-458.
Gyftopoulos, E.P. & Hatsopoulos, G.N.: 1968, ‘Quantum-thermodynamic definition of electronegativity’, Proceedings of the National Academy of Sciences USA, 60, 786-93.
Hohenberg, P. & Kohn, W.: 1964, ‘Inhomogeneous electron gas’, Physical Review, 136, B864-71.
Kohn, W. & Sham, L.J.: 1965, ‘Self-consistent equations including exchange and correlation effects’, Physical Review, 140, A1133-8.
Levy, M.L.: 1979, ‘Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem’ Proceedings of the National Academy of Sciences USA, 76, 6062-5.
Liu, S.: 1996, ‘Expansions of the pair distribution function and the second-order density matrix in terms of homogeneous functionals’, Physical Review A, 54, 4863-7.
March, N.H. & Parr, R.G.: 1980, ‘Chemical potential, Teller’s theorem, and the scaling of atomic and molecular energies’, Proceedings of the National Academy of Sciences USA, 77, 6285-8.
March, N.H.: 1982, ‘Electron density theory of atoms and molecules’, The Journal of Physical Chemistry, 86, 2262-7.
Mezey, P.G.: 1999, ‘The holographic electron density theorem and quantum similiarity measures’, Molecular Physics, 96, 169-78.
Mulliken, R.S.: 1934, ‘A new electroaffinity scale; together with data on valence states and on valence ionization potentials and electron affinities’, The Journal of Chemical Physics, 2, 782-93.
Nagy, A. & March, N.H.: 1991, ‘The exact form of the Pauli potential for the ground state of two- and three-level atoms and ions’, International Journal of Quantum Chemistry, 34, 615-23.
Parr, R.G. & Pearson, R.G.: 1983, ‘Absolute hardness: Companion parameter to absolute electronegativity’, Journal of the American Chemical Society, 105, 7512-6.
Parr, R.G. & Yang, W.: 2000, ‘Density functional approach to the frontier-electron theory of chemical reactivity’, Theoretical Chemistry Accounts, 103, 353-60.
Pauling, L.: 1932, ‘The nature of the chemical bond. IV. The energy of single bonds and the relative electronegativity of atoms’, Journal of the American Chemical Society, 54, 3570-82.
Pearson, R.G.: 1963, ‘Hard and soft acids and bases’, Journal of the American Chemical Society, 85, 3533-9.
Pearson, R.G.: 1994, ‘Principle of maximum physical hardness’, The Journal of Physical Chemistry, 98, 1989-92.
Pearson, R.G.: 1997, Chemical hardness, New York: Wiley, pp. 1-198.
Perdew, J.P.; Parr, R.B.; Levy, M. & Balduz, H.L.: 1982, ‘Density-functional theory for fractional particle number: derivative discontinuities of the energy’, Physical Review Letters, 49, 1691-4.
Primas, H.: 1967, ‘A density functional representation of quantum chemistry. I. Motivation and general formalism’, International Journal of Quantum Chemistry, 1, 493-519.
Sanderson, R.T.: 1951, ‘An interpretation of bond lengths and a classification of bonds’, Science, 114, 670-2.
11. Group-theoretic methodology
Ballhausen, C.J.: 1962, Introduction to ligand field theory, New York: McGraw-Hill, pp. 1-320.
Bethe, H.A.: 1929, ‘Splitting of terms in crystals’, Annalen Physik, 3, 133-208.
Bochvar, D.A.; Stankevich, I.V. & Chistyakov, A.L.: 1961, ‘Energy levels of truly alternant systems’, Russian Journal of Physical Chemistry, 35, 656-8.
Bunker, P.R. & Jensen, P.: 1998, Molecular Symmetry and Spectroscopy, Ottawa: NRC Research Press, pp. 1-752.
Cooper, I.L. & McWeeny, R.: 1966, ‘Studies in configuration interaction. I.’, The Journal of Chemical Physics, 45, 226-34.
Cotton, F.A.: 1963, Chemical applications of group theory, New York: Interscience, pp. 1-295 (and later editions of 1971 & 1990).
Coulson, C.A. & Rushbrooke, G.S.: 1940, ‘Note on the method of molecular orbitals’, Mathematical Proceedings of the Cambridge Philosophical Society, 36, 193-200.
Ezra, G.S.: 1982, Symmetry properties of molecules, Berlin: Springer Verlag, pp. 1-202.
Frei, H., Groner, P., Bauder, A. & Gunthard, H.H.: 1978, ‘Isometric group of semi-rigid models: Relation to the permutation-inversion group and extension of the concept to non-rigid molecules’, Molecular Physics, 36, 1469-95.
Griffith, J.S.: 1962, The irreducible tensor method for molecular symmetry groups, Englewood Cliffs: Prentice-Hall, pp. 1-134.
Hartmann, H. & Schläfer, H.L.: 1951, ‘Colour and constitution of complex compounds. II. Light absorption of complex ions of Ti(III)’, Zeitschrift für Physikalische Chemie, 197, 116-42.
Hartmann, H. & Schläfer, H.L.: 1954, ‘Farbe und Konstitution von Komplexverbindungen der Übergangselemente’, Angewandte Chemie, 66, 768-76.
Hubbard, L.M.; Wulfman, C. & Rabitz, H.: 1986, ‘Parameter space mapping of first-order linear ordinary differential equations’, The Journal of Physical Chemistry, 90, 2273-80.
Iachello, F. & Levine, R.D.: 1995, Algebraic theory of molecules, Oxford: Oxford University Press, pp. 1-272.
Iachello, F. & Oss, S.: 1996, ‘Algebraic approach to molecular spectra: Two-dimensional problems’, The Journal of Physical Chemistry, 104, 6956-63.
Iachello, F.: 1997, ‘Lie algebraic methods in molecular spectroscopy’, Trends in Chemical Physics, 5, 1-24.
Jeziorski, B.; Paldus, J. & Jankowski, P.: 1995, ‘Unitary group approach to spin-adapted open-shell coupled cluster theory’, International Journal of Quantum Chemistry, 56, 129-55.
Kaplan, I.G.: 1975, Symmetry of many-electron systems, New York: Academic Press, pp. 1-370.
Klein, D.J. & Zivkovic, T.P.: 1990, ‘Graphical and color-pairing symmetries’, International Journal of Quantum Chemistry, 37, 423-36.
Koutecky, J., Paldus, J. & Čížek, J.: 1985, ‘Alternancy symmetry: A unified viewpoint’, Journal of Chemical Physics, 83, 1722-35.
Koutecky, J.: 1966, ‘Contribution to the theory of alternant systems’, The Journal of Chemical Physics, 44, 3702-6.
Levine, R.D.: 1982, ‘Representation of one-dimensional in a Morse oscillator by a quadratic Hamiltonian’, Chemical Physics Letters, 95, 87-90.
Liehr, A.D.: 1960, ‘Reciprocation of electrostatic and electromagnetic forces in ligand field theory’, The Journal of Physical Chemistry, 64, 43-51.
Litvin, D.B. & Opechowski, W.: 1974, ‘Spin symmetries’, Physica, 76, 538-54.
Longuet, H.C.: 1963, ‘The symmetry groups of non-rigid molecules’, Molecular Physics, 6, 445-60.
MacLachlan, A.D.: 1959, ‘The pairing of electronic states in alternant hydrocarbons’, Molecular Physics, 2, 271-84.
Matsen, F.A.: 1964, ‘Spin-free quantum chemistry’, Advances in Quantum Chemistry, 1, 59-114.
Matsen, F.A. & Pauncz, R.: 1986, The unitary group in quantum chemistry, Amnsterdam: Elsevier, p. 1-391.
Matsen, F.A.: 1987, ‘Spin-free quantum chemistry. XXIII. The generator-state approach’, International Journal of Quantum Chemistry, 32, 71-86.
Matsen, F.A.: 1992, ‘Gel’fand structures: Primitive patterns of understanding’, Journal of Molecular Structure: THEOCHEM, 259, 65-81.
Nefedova, V.V.; Boldyrev, A.I. & Simons, J.: 1993, ‘Graphical description of the symmetries of potential energy surfaces’, Journal of Chemical Physics, 98, 8801-9.
Opechowski, W.: 1980, ‘Remarks on metacrystallagraphic groups’, MATCH Communications in Mathematical and in Computer Chemistry, 9, 51-64.
Paldus, J.: 1974, ‘Group theoretical approach to the configuration interaction and perturbation theory calculations for atomic and molecular systems’, The Journal of Chemical Physics, 61, 5321-30.
Paldus, J.: 1975, ‘Pattern calculus for the unitary group approach to the electronic correlation problem’, International Journal of Quantum Chemistry, 9, 165-74.
Paldus, J. & Jeziorski, B.: 1988, ‘Clifford algebra and unitary group formulations of the many-electron problem’, Theoretica Chimica Acta, 73, 81-103.
Paldus, J.; Rettrup, S. & Sarma, C.R.: 1989, ‘Clifford algebra realization of Rumer-Weyl basis’, Journal of Molecular Structure: THEOCHEM, 58, 85-101.
Pauncz, R.: 1995, The symmetric group in quantum chemistry, Florida: CRC, pp. 1-330.
Serre, J.: 1974, ‘Symmetry of non-rigid molecules’, Advances in Quantum Chemistry, 8, 1-36.
Simonetta, M.; Gianinetti, E. & Vandoni, I.: 1968, ‘Valence-bond theory for simple hydrocarbon molecules, radicals, and ions’, The Journal of Chemical Physics, 48, 1579-94.
Weyl, H.: 1928, Gruppentheorie und Quantenmechanick, Leipzig: Hirzel, pp. 1-288.
Wigner, E.P.: 1931, Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomspektren, Braunschweig: Vieweg, pp. 1-332.
Wulfman, C.E. & Takahata, Y.: 1967, ‘Noninvariance groups in molecular quantum mechanics. I.’ The Journal of Chemical Physics, 47, 488-98.
Wulfman, C.E.: 1998, ‘Dynamical symmetries of Schroedinger equations and geometrical symmetries of classical total energy surfaces’, The Journal of Physical Chemistry A, 103, 9542-8.
Yutsis, A.P.; Levinson, I.B.; Vanagas, V.V.: 1962, Mathematical apparatus of the theory of angular momentum, Washintong D.C.: National Science Foundation, pp. 1-158.
12. Molecular dynamics
Avron, J.E.; Berger, J.: 1998, ‘The Longuet-Higgins phase and charge transport in molecular rings’, Chemical Physics Letters, 294, 13-18.
Ben, A., Levine; R.D. & Bernstein, R.B.: 1972, ‘Product state distribution in exoergic chemical reactions and the concept of temperature’, Chemical Physics Letters, 15, 160-4.
Bernstein, R.B.: 1972, ‘Entropy and chemical change. I. Characterization of product (and reactant) energy in reactive molecular collisions: Information and entropy deficiency’, Journal of Chemical Physics, 57, 434-49.
Broeckhove, J.; Claessens, M.; Lathouwers, L.; Van Leuven, P.; Deumens, E. & Öhrn, Y.: 1990, ‘Applications of the generator coordinate approximation to diatomic systems. III. Curve-crossing problems’, Journal of Chemical Physics, 93, 8945-53.
Diz, A.; Deumens, E. & Öhrn, Y.: 1990, ‘Quantum electron-nuclear dynamics’, Chemical Physics Letters, 166, 203-10.
Eyring, H. & Polyani, M.: 1931, ‘On simple gas reaction’, Zeitschrift für physikalische Chemie B, 12, 279-311.
Fukui, K.: 1981, ‘The path of chemical reactions – the IRC approach’, Accounts of Chemical Research, 14, 363-8.
Heidrich, D.: 1995, The reaction path in chemistry: Current approaches and perspectives, Amsterdam: Kluwer, pp. 1-299.
Heller, E.J.: 1977, ‘Phase space interpretation of semiclassical theory’, Journal of Chemical Physics, 67, 3339-51.
Heller, E.J.: 1981, ‘The semiclassical way to molecular spectroscopy’, Accounts of Chemical Research, 14, 368-75.
Herzberg, G. & Longuet, H.C.: 1963, ‘Intersection of potential energy surfaces in polyatomic molecules’, Faraday Discussions of the Chemical Society, 35, 77-82.
Ho, T.S. & Rabitz, H.: 1996, ‘A general method for construction multidimensional molecular potential energy surfaces from ab initio calculations’, Journal of Chemical Physics, 104, 2584-97.
Jahn, H.A. & Teller, E.: 1937, ‘Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy’ Proceedings Royal Society A, 161, 220-35.
Levine, R.D. & Bernstein, R.B.: 1973, ‘Energy disposal and energy requirements for elementary chemical reactions’, Faraday Discussions of the Chemical Society, 55, 100-12.
Liehr, A.D.: 1963a, ‘Topological aspects of the electronic stability problem. Part I. Degenerate electronic states’, The Journal of Physical Chemistry, 67, 389-471.
Liehr, A.D.: 1963b, ‘Topological aspects of the electronic stability problem. Part II. Non-degenerate electronic states’, The Journal of Physical Chemistry, 67, 471-94.
Light, J.C. & Walker, R.B.: 1976, ‘An R-Matrix approach to the solution of coupled equations for atom-molecule reactive scattering’, Journal of Chemical Physics, 65, 4272-82.
Lill, J.V.; Schmalz, T.G. & Light, J.C.: 1983, ‘Imbedded Green’s functions in atomic and molecular scattering theory’, Journal of Chemical Physics, 78, 4456-61.
Longuet, H.C.; Opik, U.; Pryce, M.H.L. & Sack, R.A.: 1958, ‘Studies of the Jahn-Teller effect. II. The dynamical problem’, Proceedings Royal Society A, 244, 1-16.
Marcus, R.A.: 1964, ‘Generalization of the activated complex theory of reaction rates. I. Quantum mechanical treatment’, Journal of Chemical Physics, 41, 2614-23.
Marcus, R.A.: 1964, ‘Generalization of the activated complex theory of reaction rates. II. Classical mechanical treatment’, Journal of Chemical Physics, 41, 2624-33.
Marcus, R.A.: 1979, ‘Vibrational nonadiabaticity and tunneling effects in transition state theory’, The Journal of Physical Chemistry, 83, 204-07.
McNutt, J.F. & Wyatt, R.E.: 1979, ‘Generalized hyperbolic coordinates for colinear reactive scattering’, Journal of Chemical Physics, 70, 5307-12.
Meade, C.A. & Truhlar, D.G.: 1979, ‘On the determination of Born-Oppenheimer nuclear motion wave functions including complications due conical intersections and identical nuclei’, Journal of Chemical Physics, 70, 2284-96.
Meade, C.A.: 1980, ‘The molecular Aharonov-Bohm effect in bound states’, Chemical Physics, 49, 23-32.
Mezey, P.G.: 1987, Potential energy hypersurfaces, Amsterdam: Elsevier, pp. 1-538.
Miller, W.H.; Handy, N.C. & Adams, J.E.: 1980, ‘Reaction path Hamiltonian for polyatomic molecules’, Journal of Chemical Physics, 72, 99-112.
Moon, F.C.: 2004, Chaotic vibrations: An introduction for applied scientists and engineers, New York: Wiley, pp. 1-309.
Murrell, J.N.: 1977, ‘The potential energy surfaces of polyatomic molecules’, Structure and Bonding, 32, 93-146.
Nesbet, R.K.: 1981, ‘Surprisal theory’, in: D. Henderson (ed.), Theoretical Chemistry – Advances and Perspectives, Volume 6, New York: Academic Press Inc., pp. 79-126.
Pearson, R.G.: 1969a, ‘Symmetry rule for predicting molecular structure & reactivity’, Journal of the American Chemical Society, 91, 1252-4.
Pearson, R.G.: 1969b, ‘A symmetry rule for predicting molecular structure’, Journal of the American Chemical Society, 91, 4947-55.
Pechukas, P.: 1982, ‘Kolmogorov entropy and ‘quantum chaos’’, The Journal of Physical Chemistry, 86, 2239-43.
Remacle, F. & Levine, R.D.: 1991, ‘The maximum entropy of an optical spectrum and the redistribution in phase space’, Chemical Physics Letters, 181, 307-11.
Schwenke, D.W.; Truhlar, D.G. & Kouri, D.J.: 1987, ‘Propagation method for the coupling channel arrangement equations for reactive scattering in three dimensions’, Journal of Chemical Physics, 86, 2772-86.
Wigner, E.P.: 1937, ‘Calculation of the rate of elementary association reactions’, Journal of Chemical Physics, 5, 720-5.
Wyatt, R.E. & Zhang, J.Z.H.: 1996, Dynamics of molecules and chemical reactions, New York: Marcel Dekker, pp. 1-704.
Zilberg, S. & Haas, Y.: 2000, ‘Conical intersections in molecular photochemistry – the role of phase change’, Journal of Chemical Physics, 259, 249-61.
13. Solid-state chemistry
Burdett, J.K. & McLarnan, T.J.: 1982, ‘Geometrical and electronic links among the structures of MX2 solids: Structural enumeration and electronic stability of pyrite-like systems’, Inorganic Chemistry, 21, 1119-28.
Burdett, J.K. & Lee, S.: 1985, ‘Moments and the energies of solids’, Journal of the American Chemical Society, 107, 3050-63.
Burdett, J.K.: 1988, ‘Topological control of the structures of molecules and solids’, Accounts of Chemical Research, 21, 189-94.
Burdett, J.K.; Gramsch, S.A.; Stephen, A. & Smith, L.: 1996a, ‘Some factors influencing metal-insulator transitions’, Zeitschrift für Anorganische und Allgemeine Chemie, 622, 1667-76.
Burdett, J.K.: 1996b, ‘Electronic structure and properties of solids’, The Journal of Physical Chemistry, 100, 13263-74.
Hoffmann, R.: 1988, Solids and surfaces: A chemist’s view of bonding in extended structures, Weinheim: VCH, pp. 1-152.
Klein, D.J. & Seitz, W.A.: 1974, ‘Partially filled linear Hubbard model near the atomic limit’, Physical Review B, 10, 3217-26.
Krugler, J.L.; Montgomery, C.G. & McConnell, H.M.: 1964, ‘Collective electronic states in molecular crystals’, Journal of Chemical Physics, 41, 2421-8.
Lee, S.: 1990, ‘Projection operator Hückel method and antiferromagnetism’, Journal of the American Chemical Society, 112, 6777-83.
Longuet, H.C. & Salem, L.: 1959, ‘Alternation of bond lengths in long conjugated chain molecules’, Proceedings Royal Society A, 251, 172-85.
McConnell, H.M. & Soos, Z.G.: 1964, ‘Phonon-coupled interactions between paramagnetic excitons’, Journal of Chemical Physics, 40, 586-8.
Merrifield, R.E.: 1958, ‘Propagation of electronic excitation in insulating crystals’, Journal of Chemical Physics, 28, 647-50.
Pople, J.A. & Walmsley, S.J.: 1962, ‘Bond alternation defects in long polyene molecules’, Molecular Physics, 5, 15-20.
Soos, Z.G.: 1965, ‘Theory of the linear Heisenberg antiferromagnet. Application to paramagnetic excitations in organic crystals’, Journal of Chemical Physics, 43, 1121-40.
Soos, Z.G. & Strebel, P.G.: 1970, ‘Theory of charge transfer in aromatic donor-acceptor crystals’, Journal of Chemical Physics, 53, 4077-90.
Soos, Z.G.; Ducasse, L.R. & Metzger, R.M.: 1982, ‘Partial ionicity, cohesion, and charge correlations in narrow-band solids’, Journal of Chemical Physics, 77, 3036-45.
Su, W.; Schreiffer, J.R. & Heeger, A.J.: 1980, ‘Soliton dynamics in polyacetylene’, Physical Review B, 22, 2099-111.
Zhu, H.Y.; Balaban, A.T.; Klein, D.J. & Zivković, T.P.: 1994, ‘Conjugated circuit computations on two-dimensional carbon networks’, Journal of Chemical Physics, 101, 5281-92.
14. Stereochemistry
Buda, A.B.; Auf der Heyde, T.P.E. & Mislow, K.: 1991, ‘Geometric chriality products’, Journal of Mathematical Chemistry, 6, 243-53.
Crawford, B.L.; Wilson, E.B.: 1941, ‘The normal vibrations of molecules with internal torsional motions’, Journal of Chemical Physics, 9, 323-29.
Dickerson, R.E. & Lipscomb, W.N.: 1957, ‘Semitopological approach to boron-hydride structures’, Journal of Chemical Physics, 27, 212-17.
Dress, A.: 1979, ‘Eine Bemerkung zur Ruch-Schönhofer’schen Halbordunung von Young-Diagrammen’, MATCH Communications in Mathematical and in Computer Chemistry, 7, 317-25.
Flapan, E.: 2000, When topology meets chemistry, New York: Cambridge University Press, pp. 1-241.
Havel, T.F. & Crippen, G.M.: 1988, Distance geometry and molecular conformation, New York: Research Studies Press, pp. 1-541.
Johnston, R.L. & Mingos, D.M.P.: 1986, ‘Molecular orbital calculations relevant to the hyper-closo vs. iso-closo controversy in metallaboranes’, Inorganic Chemistry, 25, 3321-3.
Kilpatrick, J.E.; Pitzer, K.S. & Spitzer, R.: 1947, ‘The thermodynamics and molecular structure of cyclopentane’, Journal of the American Chemical Society, 69, 2483-8.
King, R. B.: 1991, ‘Chirality algebra’, in: P.G. Mezey (ed.), New developments in molecular chirality, Dordrecht: Kluwer Academic Publishers, pp. 131-64.
Liang, C. & Mislow, K.: 1994, ‘Classification of topological chiral molecules’, Journal of Mathematical Chemistry, 15, 245-60.
Lipscomb, W.N.: 1958, ‘Possible boron hydride ions’, The Journal of Physical Chemistry, 62, 381-2.
Lipscomb, W.N.: 1973, ‘Three-center bonds in electron-deficient compounds. The localized molecular orbital approach’, Accounts of Chemical Research, 6, 257-62.
Meade, A.: 1974, ‘Permutation groups, symmetry, and chirality in chemistry’, Topics in Current Chemistry, 49, 1-88.
Mezey, P.G.: 1993, Shape in chemistry: An introduction to molecular shape and topology, Amsterdam: Elsevier, pp. 1-224.
Mingos, D.M.P. & Johnston, R.L.: 1987, ‘Theoretical models of cluster bonding’, Structure and Bonding, 68, 29-87.
Mislow, K.: 1977, ‘On the classification of pairwise relations between isomeric structures’, Bulletin des Sociétés Chimiques Belges, 86, 595-01.
Pauling, L.: 1931, ‘The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules’, Journal of the American Chemical Society, 53, 1367-400.
Ruch, E. & Schönhofer, A.: 1970, ‘Theorie der Chistalitätsfuntionen’, Theoretica Chimica Acta, 19, 225-87.
Rudolph, R.W. & Pretzer, W.R.: 1972, ‘Hückel-type rules and the systematization of borane and heteroborane chemistry’, Inorganic Chemistry, 11, 1974-8.
Rudolph, R.W.: 1976, ‘Boranes and heteroboranes: A paradigm for the electron requirements of clusters?’, Accounts of Chemical Research, 9, 446-52.
Simon, J.: 1978, ‘A topological approach to the stereochemistry of nonrigid molecules’, in: R.B. King & D.H. Rouvray (eds.), Graph theory and topology in chemistry, Amsterdam: Elsevier, pp. 43-75.
Sippl, M.J. & Scheraga, H.A.: 1986, ‘Cayley-Menger coordinates’, Proceedings of the National Academy of Sciences of the United States of America, 83, 2283-7.
Stone, A.J. & Alderton, M. J.: 1982, ‘A new model of structure and bonding in the boron hydrides’, Inorganic Chemistry, 21, 2297-302.
Ugi, I.; Marquarding, D.; Klusacek, H.; Gokel, G. & Gillespie, P.: 1970, ‘Chemistry and logical structures’, Angewandte Chemie International Edition, 9, 703-30.
Walba, D.M.: 1991, ‘A topological hierarchy of molecular chirality and other tidbits in topological stereochemistry’, P.G. Mezey (ed.), New developments in molecular chirality, Dordrecht: Kluwer Academic Publishers, pp. 119-29.
Williams, R.E.: 1992, ‘The polyborane, carborane, carbocation continuum: Architectural patterns’, Chemical Reviews, 92, 177-207.
Wilson, E.B.: 1935, ‘Symmetry considerations concerning the splitting of vibration-rotation levels in polyatomic molecules’, Journal of Chemical Physics, 3, 818-21.
Zabrodsky, H.; Peleg, S. & Avnir, D.: 1992, ‘Continuous symmetry measures’, Journal of the American Chemical Society, 114, 7843-51.
15. Polymer statistics
Avnir, D.: 1987, ‘The geometry factor in photoprocesses on irregular (fractal) surfaces. 1. Static considerations’, Journal of the American Chemical Society, 109, 2931-8.
Brazhnik, O.D. & Freed, K.F.: 1996, ‘Application of graph theory to the statistical thermodynamics of lattice polymers. I. Elements of theory and test for dimers’, Journal of Chemical Physics, 105, 837-61.
Brender, C.; Ben, D. & Havlin, S.: 1983, ‘Study of Monte Carlo methods for generating self-avoiding walks’, Journal of Statistic Physics, 31, 661-70.
DeGennes, P.G.: 1979, Scaling concepts in polymer physics, Ithaca: Cornell University Press, pp. 1-319.
Ercolani, G.: 1998, ‘Physical basis of self-assembly macrocyclizations’, The Journal of Physical Chemistry, 102, 5699-703.
Fischer, M. & Vögtle, F.: 1999, ‘Dendrimers: From design to application – a progress report’, Angewandte Chemie International Edition, 38, 884-905.
Flory, P.J.: 1953, Fundamentals of polymer chemistry, Ithaca: Cornell University Press, pp. 1-688.
Flory, P.J.: 1969, Statistical mechanics of chain molecules, New York: Interscience Publishers, pp. 1-432.
Freed, K.F.: 1971, ‘Self-consistent field theories of the polymer excluded volume problem. I. Edwards’ functional integral approach’, Journal of Chemical Physics, 35, 3910-21.
Heath, J.R., Kuekes; P.J.; Snider, G.S. & Williams, R.S.: 1998, ‘A defect-tolerant computer architecture: Opportunities for nanotechnology’, Science, 280, 1716-21.
Kirkwood, J.G.: 1996, ‘The general theory of irreversible processes in solutions of macromolecules’, Journal of Polymer Science, 34, 1-14.
Klein, D.J.: 1980, ‘Distributions for self-avoiding walks on strips, cylinders, and tubes’, Journal of Statistical Physics, 23, 561-86.
Kosmas, M.K. & Freed, K.F.: 1978, ‘On scaling theories of polymer solutions’, Journal of Chemical Physics, 69, 3647-59.
Kuchanov, S.I.; Koralev, S.V. & Panyukov, S.V.: 1988, ‘Graph in chemical physics of polymers’, Advances in Chemical Physics, 72, 115-326.
Montroll, E.W.: 1950, ‘Markoff chains and excluded volume effect in polymer chains’, Journal of Chemical Physics, 18, 734-43.
Pfeiffer, P. & Avnir, D.: 1983, ‘Chemistry in noninteger dimensions between two and three. I. Fractal theory of heterogeneous surfaces’, Journal of Chemical Physics, 79, 3558-65.
Rachovsky, S. & Scheraga, H.A.: 1980, ‘Differential geometry and polymer conformation. 2. Development of a conformational distance function’, Macromolecules, 13, 1440-53.
Seitz, W.A. & Klein, D.J.: 1981, ‘Monte Carlo results for a branched polymer model including volume exclusion’, Journal of Chemical Physics, 77, 5190-3.
Seri, A. & Avnir, D.: 1993, ‘Kinetrics of diffusion-limited adsorption on fractal surfaces’, The Journal of Physical Chemistry, 97, 10380-4.
Stang, P.J. & Olenyuk, B.: 1977, ‘Self-assembly, symmetry, and molecular architecture: Coordination as the motif in the rational design of supramolecular metallacyclic polygons and polyhedra’, Accounts of Chemical Research, 30, 502-18.
Sumners, D.W. & Whittington, S.G.: 1988, ‘Knots in self-avoiding walks’, Journal of Physics A, 21, 1689-94.
Tomalia, D.A.; Naylor, A.M. & Goddard, W.A.: 1990, ‘Starburst dendrimers: Molecular-level control of size, shape, surface chemistry, topology, and flexibility from atoms to macroscopic matter’, Angewandte Chemie International Edition, 29, 138-75.
Tomalia, D.A.: 2005, ‘Birth of a new macromolecular architecture: Dendrimers as quantized building blocks for nanoscale syntehetic polymer chemistry’, Progress Polymer Science, 30, 294-324.
Wall, F.T.; Hiller, L.A. & Wheeler, D.J.: 1954, ‘Statistical Computation of Mean Dimensions of Macromolecules. I.’, Journal of Chemical Physics, 22, 1036-41.
Wall, F.T. & Mandel, F.: 1975, ‘Macromolecular dimensions obtained by an efficient Monte Carlo method without sample attrition’, Journal of Chemical Physics, 63, 4592-5.
Yamakawa, H.: 1968, ‘Asymptotic solution of the excluded-volume problem in a linear polymer chain’, Journal of Chemical Physics, 48, 3845-9.
16. Chemical reaction-network analysis
Baerbel, M.R. & Stadler, P.F.: 2002, ‘Generalized topological spaces in evolutionary theory and combinatorial chemistry’, Journal of Chemical Information and Computer Sciences, 42, 577-85.
Balaban, A.T.: 1994, ‘Reaction graphs’, in: D. Bonchev & O. Mekenyan (eds.), Graph theoretical approaches to chemical reactivity, Dordrecht: Springer Science, pp.137-80.
Balaban, A.T.; Farcasiu, D. & Banica, R.: 1966, ‘Chemical graphs. II. Graphs of multiple 1,2-shifts in carbonium ions and related systems’, Revue Roumaine de Chimie, 11, 1205-27.
Barabási, A.L.: 2012, ‘The network takeover’, Nature Physics, 8, 14-16.
Benkoe, G.; Flamm, C. & Stadler, P.F.: 2003, ‘A graph-based toy model of chemistry’, Journal of Chemical Information and Computer Sciences, 43, 1085-93.
Corey, E.J.; Jeffrey, W. & David, A.: 1974, ‘Computer-assisted synthetic analysis. Methods for machine generation of synthetic intermediates involving multistep look-ahead’, Journal of the American Chemical Society, 96, 7724-37.
Corey, E.J. & Jorgensen, W.L.: 1977, ‘Computer-assisted synthetic analysis. Synthetic strategies based on appendages and the use of reconnective transforms’, Journal of the American Chemical Society, 98, 189-03.
Cracium, G. & Feinberg, M.: 2005, ‘Multiple equilibria in complex chemical reaction networks: I’, SIAM Journal on Applied Mathematics, 65, 1526-46.
Cracium, G. & Feinberg, M.: 2006, ‘Multiple equilibria in complex chemical reaction networks: II’, SIAM Journal on Applied Mathematics, 66, 1321-38.
Crutchfield, J.P.: 2012, ‘Between order and chaos’, Nature, 8, 17-24.
Dubois, J.E.: 1973, ‘DARC system in chemistry’, in: W.T. Wipke (ed.), Computer representation and manipulation of chemical information, New York: John Wiley & Sons, pp. 239-63.
Dugundji, J. & Ugi, I.: 1973, ‘An algebraic model of constitutional chemistry as a basis for chemical computer programs’, Topics in Current Chemistry, 39, 19-64.
Estrada, E.; Higham, D.J.; Fox, M. & Oppo, G.L.: 2010, Network science: Complexity in nature and technology, Berlin: Springer, pp. 1-256.
Feinberg, M.: 1972, ‘Complex balancing in general kinetic systems’, Archive for Rational Mechanics and Analysis, 49, 187-94.
Feinberg, M.: 1989, ‘Necessary and sufficient conditions for detailed balancing in mass action systems of arbitrary complexity’, Chemical Engineering Science, 44, 1819-27.
Fujita, S.: 2001, Computer-oriented representation of organic reactions, Kyoto: Yoshioka Shoten, pp. 1-371.
Gao, J.; Buldyrev, S.V.; Stanley, H.E. & Havlin, S.: 2002, ‘Networks formed from interdependent networks’, Nature Physics, 8, 40-8.
Hendrickson, J.B.: 1976, ‘A general protocol for systematic synthesis design’, Topics Current Chemistry, 62, 49-172.
Hendrickson, J.B.: 1986, ‘Approaching the logic of synthesis design’, Accounts of Chemical Research, 19, 274-81.
Hendrickson, J.B. & Toczko, A.G.: 1989, ‘SYNGEN program for synthesis design: Basic computing techniques’, Journal Chemical Information and Computer Sciences, 29, 137-45.
Horn, F. & Jackson, R.: 1972a, ‘General mass action kinetics’, Archive for Rational Mechanics and Analysis, 47, 81-116.
Horn, F.: 1972b, ‘Necessary and sufficient conditions for complex balancing in chemical kinetics’, Archive for Rational Mechanics and Analysis, 49, 172-86.
Ivanciuc, T. & Klein, D.J.: 2004, ‘Parameter-free structure-property correlation via progressive reaction posets for substituted benzenes’, Journal of Chemical Information and Computer Sciences, 44, 610-17.
Ivanciuc, T.; Ivanciuc, O. & Klein, D.J.: 2011, ‘Network-QSAR with reaction poset quantitative superstructure-activity relationships (QSSAR) for PCB chromatographic properties’, Current Bioinformatics, 6, 25-34.
Joshi, R. & Shiu, A.: 2013, ‘Atoms of multistationarity in chemical reaction networks’, Journal of Mathematical Chemistry, 51, 153-78.
Newman, M.E.J.: 2012, ‘Communities, modules and large-scale structure in networks’, Nature Physics, 8, 25-31.
Rouvray, D.H. & Bonchev, D.: 2003, Mathematical chemistry. Volume VII, Complexity in Chemistry, London: Taylor and Francis, pp. 1-208.
Spann, M.L.; Chu, K.C.; Todd, W. & Ouchi, G.: 1978, ‘Use of computerized methods to predict metabolic pathways and metabolites’, Journal of Environmental Pathology, Toxicology and Oncology, 2, 123-31.
Stadler, P.F.; Schnabl, W.; Forst, C.V. & Schuster, P.: 1995, ‘Dynamics of small autocatalytic reaction networks. II. Replication, mutation and catalysis’, Bulletin of Mathematical Biology, 57, 21-61.
Stadler, P.F.: 1996, ‘Landscapes and their correlation functions’, Journal Mathematical Chemistry, 20, 1-45.
Tratch, S.S.; Molchanova, M.S. & Tratch, N.S.: 2002, ‘The ARGENT program system: A second-generation tool aimed at combinatorial search for new types of oragnic reactions. 2. Mathematical models in ARGENT-1’, MATCH Communications in Mathematical and in Computer Chemistry, 46, 275-301.
Ugi, I. & Gillespie, P.D.: 1971, ‘Representation of chemical systems and interconversions by be matrices and their transformation properties’, Angewandte Chemie International Edition, 10, 914-7.
Vespignani, A.: 2012, ‘Modelling dynamical processes in complex socio-technical systems’, Nature Physics, 8, 32-9.
Wipke, W.T. & Rogers, D.: 1984, ‘Artificial intelligence in organic synthesis. SST: Starting material selection strategies. An application of superstructure search’, Journal of Chemical Information and Computer Sciences, 24, 71-81.
Wipke, W.T. & Vladutz, G.: 1990, ‘An alternative view of reaction similarity: Citation analysis’, Tetrahedron Computer Methodology, 3, 83-107.
Zefirov, N.S.; Tratch, S.S. & Molchanova, M.S.: 2002, ‘The ARGENT program system: A second-generation tool aimed at combinatorial search for new types of oragnic reactions.1. Main concepts and potentialities’, MATCH Communications in Mathematical and in Computer Chemistry, 46, 253-73.
17. Chemical nanotechnology
Aihara, J.I.; Yamabe, T. & Hosoya, H.: 1994, ‘Aromatic character of graphite and carbon nanotubes’, Synthetic Metals, 64, 309-13.
Amendola, V.; Fabbrizzi, L.; Mangano, C.; & Pallavicini, P.: 2001, ‘Molecular machines based on metal ion translocation’, Accounts of Chemical Research, 34, 488-93.
Ballardini, R.; Balzani, V.; Credi, A.; Gandolfi, M.T. & Venturi, M.: 2001, ‘Artificial molecular-level machines: Which energy to make them work?’, Accounts of Chemical Research, 34, 445-55.
Brinkmann, G.; Fowler, P.W.; Manolopoulos, D.E. & Palser, A.H.R.: 1999, ‘A census of nanotube caps’, Chemical Physics Letters, 315, 335-47.
Bustamante, C.; Keller, D. & Oster, G.: 2001, ‘The physics of molecular motors’, Accounts of Chemical Research, 34, 412-20.
Collin, J-P.; Dietrich-Buchecker, C.; Gaviña, P.; Jimenez-Molero, M.C. & Sauvage, J-P.: 2001, ‘Shuttles and muscles: Linear molecular machines based on transition metals’, Accounts of Chemical Research, 34, 477-87.
Dietrich, C.O. & Sauvage, J.P.: 1987, ‘Interlocking of molecular threads: From the statistical approach to the templated synthesis of catenands’, Chemical Reviews, 87, 795-810.
Dobrowlski, J.C.: 2002, ‘On the belt and Moebius isomers of the coronene molecule’, Journal of Chemical Information and Computer Sciences, 42, 490-9.
Ernst, C. & Sumners, D.W.: 1990, ‘A calculus for rational tangles: Applications to DNA recombination’, Mathematical Proceedings of the Cambridge Philosophical Society, 108, 489-15.
Feringa, B.L.: 2001, ‘In control of motion: From molecular switches to molecular motors’, Accounts of Chemical Research, 34, 504-13.
Fisher, M.E. & Kolomeisky, A.B.:1999, ‘The force exerted by a molecular motor’, Proceedings of the National Academy of Sciences of the United States of America, 96, 6597-602.
Flynn, G.W.: 2011, ‘The dawning of the age of graphene’, Journal of Chemical Physics, 135, 050901.
Frisch, H.L. & Wasserman, E.: 1961, ‘Chemical topology’, Journal of the American Chemical Society, 83, 3789-95.
Harada, A.: 2001, ‘Cyclodextrin-based molecular machines’, Accounts of Chemical Research, 34, 456-64.
Jackman, R.J.; Brittain, S.T.; Adams, A.; Prentiss, M.B. & Whitesides, G.M.: 1998, ‘Design and fabrication of topologically complex, three-dimensional microstructures’, Science, 280, 2089-91.
Kelly, T.R.: 2001, ‘Progress toward a rationally designed molecular motor’, Accounts of Chemical Research, 34, 514-22.
King, R.B.: 1996, ‘Chemical applications of topology and group theory. 29. Low density polymeric carbon allotropes based on negative curvature structures’, The Journal of Physical Chemistry, 100, 15096-104.
Kirby, E.C.: 1993a, ‘Cylindrical and toroidal polyhex structures’, Croatica Chemica Acta, 66, 13-26.
Kirby, E.C.; Mallion, R.B. & Pollak, P.: 1993b, ‘Toroidal polyhexes’, Journal of the Chemical Society, Faraday Transactions, 89, 1945-53.
Klein, D.J.; Seitz, W.A. & Schmalz, T.G.: 1993, ‘Symmetry of infinite tubular polymers: Application to Buckytubes’, The Journal of Physical Chemistry, 97, 1231-6.
Klein, D.J.: 1994, ‘Elemental benzenoids’, Journal of Chemical Information and Computer Sciences, 34, 453-9.
Klein, D.J.: 2002, ‘Topo-combinatoric categorization of quasi-local graphitic defects’, Physical Chemistry Chemical Physics, 4, 2099-110.
Liang, C. & Mislow, K.: 1995, ‘Topological features of protein structures: Knots and links’, Journal of the American Chemical Society, 117, 4201-13.
Millet, K.C.: 1987, ‘Stereotopological indices for a family of chemical graphs’, Journal of Computational Chemistry, 8, 536-48.
Misra, A. & Klein, D.J.: 2002, ‘Characterization of cyclo-polyphenacenes’, Chemical Information and Computer Sciences, 42, 1171-5.
Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V. & Firsov, A.A.: 2004, ‘Electric field effect in atomically thin carbon films’, Science, 306. 666-9.
Pease, A.R.; Jeppesen, J.O.; Stoddart, J.F.; Luo, Y.; Collier, C.P. & Heath, J.R.: 2001, ‘Switching devices based on interlocked molecules’, Accounts of Chemical Research, 34, 433-44.
Rao, C.N.R.; Sood, A.K.; Subrahmanyam, K.S. & Govindaraj, A.: 2009, ‘Graphene: The new two-dimensional nanomaterial’, Angewandte Chemie International Edition, 48, 7752-77.
Schalley, C.A.; Beizai, K. & Vögtle, F.: 2001, ‘On the way to rotaxane-based molecular motors: Studies in molecular mobility and topological chirality’, Accounts of Chemical Research, 34, 465-76.
Shinkai, S.; Ikeda, M.; Sugasaki, A. & Takeuchi, M.: 2001, ‘Positive allosteric systems designed on dynamic supramolecular scaffolds: Toward switching and amplification of guest affinity and selectivity’, Accounts of Chemical Research, 34, 494-503.
Shipway, A.N. & Willner, I.: 2001, ‘Electronically transduced molecular mechanical and information functions on surfaces’, Accounts of Chemical Research, 34, 421-32.
Stoddart, J.F.: 2001, ‘Molecular machines’, Accounts of Chemical Research, 34, 410-1.
Terrones, M.; Hsu, W.K.; Hare, J.P.; Kroto, H.W.; Terrones, H. & Walton, D.R.M.: 1996, ‘Graphitic structures: From planar to spheres, toroids, and helices’, Philosophical Transaction of the Royal Society, 354, 2025-54.
18. Semi-empirical quantum chemistry
Cooper, D.: 2001, Valence bond theory, Amsterdam: Elsevier, pp. 1-836.
Coulson, C.A. & Longuet, H.C.: 1974a, ‘The electronic structure of electronic systems I’, Proceedings of the Royal Society, 191, 39-60.
Coulson, C.A. & Longuet, H.C.: 1974b, ‘The electronic structure of electronic systems II’, Proceedings of the Royal Society, 192, 16-32.
Coulson, C.A. & Longuet, H.C.: 1974c, ‘The electronic structure of electronic systems III’, Proceedings of the Royal Society, 193, 447-56.
Coulson, C.A. & Longuet, H.C.: 1974d, ‘The electronic structure of electronic systems IV’, Proceedings of the Royal Society, 193, 456-64.
Coulson, C.A. & Longuet, H.C.: 1974e, ‘The electronic structure of electronic systems V’, Proceedings of the Royal Society, 195, 188-97.
Dewar, M.J.S. & Longuet, H.C.: 1952, ‘The correspondence between the resonance and molecular orbital theories’, Proceedings of the Royal Society, 214, 482-93.
Fischer, I.: 1962, ‘Different MO approximations applied to aniline’, Arkiv for Fysik, 21, 123-43.
Fukui, K.; Yonezawa, T. & Shigu, H.: 1952, ‘A molecular orbital theory of reactivity in aromatic hydrocarbons’, Journal of Chemical Physics, 20, 722-5.
Fukui, K.: 1971, ‘Recognition of stereochemical paths by orbital interaction’, Accounts of Chemical Research, 4, 57-64.
Hoffmann, R. & Woodward, R.B.: 1965, ‘Selection rules for concerted cycloaddition reactions’, Journal of the American Chemical Society, 87, 2046-8.
Hückel, E.: 1931, ‘Quantentheoretische Beitrage zum Benzolproblem’, Zeitschrift für Physik, 70, 204-86.
Klein, D.J. & Trinajstić, N.: 1990, Valence bond theory and chemical structure, Amsterdam: Elsevier, pp. 1-629.
Linderberg, J. & Öhrn, Y.: 1968, ‘Derivation and analysis of the Pariser-Parr-Pople model’, Journal of Chemical Physics, 49, 716-27.
Longuet, H.C.: 1950a, ‘Some studies in molecular orbital theory I. Resonance structures and molecular orbitals in unsaturated hydrocarbons’, Journal of Chemical Physics, 18, 265-74.
Longuet, H.C.: 1950b, ‘Some studies in molecular orbital theory II. Ionization constants in heteroaromatic amines and related compounds’, Journal of Chemical Physics, 18, 275-82.
Longuet, H.C.: 1950c, ‘Some studies in molecular orbital theory III. Substitution in aromatic and heteroaromatic systems’, Journal of Chemical Physics, 18, 283-91.
Parisier, R. & Parr, R.G.: 1953, ‘A semi-empirical theory of the electronic spectra and electronic structure of complex unsaturated molecules: I’, Journal of Chemical Physics, 21, 466-71.
Parr, R.G.: 1964, The quantum theory of molecular electronic structure, New York: W. A. Benjamin, pp. 1-374.
Pauling, L.: 1933a, ‘The calculation of matrix elements for Lewis electronic structures of molecules’, Journal of Chemical Physics, 1, 280-3.
Pauling, L. & Wheland, G.W.: 1933b, ‘The nature of the chemical bond. V. The quantum-mechanical calculation of the resonance energy of benzene and naphthalene and the hydrocarbon free radicals’, Journal of Chemical Physics, 1, 362-74.
Pople, J.A.: 1955, ‘The electronic spectra of aromatic molecules. II: A theoretical treatment of excited states of alternant hydrocarbon molecules based on self-consistent molecular orbitals’, Proceedings of the Physical Society, 68, 81-9.
Ruedenberg, K. & Scherr, C.W.: 1953, ‘Free-electron network model for conjugated systems. I. Theory’, Journal of Chemical Physics, 21, 1565-81.
Shaik, S.S. & Hiberty, P.C.: 2007, A chemist’s guide to valence bond theory, New York: Wiley, pp. 1-316.
Woodward, R.B. & Hoffmann, R.: 1965a, ‘Stereochemistry of electrocyclic reactions’, Journal of the American Chemical Society, 87, 395-7.
Woodward, R.B. & Hoffmann, R.: 1965b, ‘Selection rules for sigmatropic reactions’, Journal of the American Chemical Society, 87, 2511-3.
Woodward, R.B. & Hoffmann, R.: 1970, The conservation of orbital symmetry, Weinheim: VCH, pp. 1-177.
19. Structure generation & enumeration
Balasubramanian, K.: 1981, ‘The combinatorics of symmetry adaptation’, Theoretica Chimica Acta, 59, 47-54.
Balasubramanian, K.: 1985, ‘Applications of combinatorics and graph theory to spectroscopy and quantum chemistry’, Chemical Reviews, 85, 599-18.
Balasubramanian, K.: 1993, ‘Generalization of de Bruijn’s extension of Pólya’s theorem to all characters’, Journal of Mathematical Chemistry, 14, 113-20.
Benecke, C.; Gruner, T.; Kerber, A.; Laue, R. & Wieland, T.: 1997, ‘Molecular structure generation with MOLGEN’, Fresenius’ Journal of Analytical Chemistry, 359, 23-32.
Brocas, J.: 1986, ‘Double cosets and enumeration of permutational isomers of fixed symmetry’, Journal of the American Chemical Society, 108, 1135-45.
Brown, H. & Masinter, L.: 1974, ‘An algorithm for the construction of the graphs of organic molecules’, Discrete Mathematics, 8, 227-44.
Buchanan, B.G. & Lederberg, J.: 1971, The heuristic dendral program for explaining empirical data, Stanford: Stanford University Press, pp. 1-22.
Bytautas, L. & Klein, D.J.: 1998, ‘Chemical combinatorics for alkane-isomer enumeration and more’, Journal of Chemical Information and Computer Sciences, 38, 1063-78.
Bytautas, L. & Klein, D.J.: 1999, ‘Alkane isomer combinatorics: Stereostructure enumeration and graph-invariant and molecular-property distributions’, Journal of Chemical Information and Computer Sciences, 39, 803-18.
Bytautas, L.; Klein, D.J. & Schmalz, T.G.: 2000, ‘All acyclic hydrocarbons: Formula periodic table and property overlap plots via chemical combinatorics’, New Journal of Chemistry, 24, 329-36.
Davidson, R.A.: 1981, ‘Isomers and isomerization: Elements of Redfield’s combinatorial theory’, Journal of the American Chemical Society, 103, 312-4.
El-Basil, S.: 2000, Combinatorial organic chemistry: An educational approach, New York: Nova Science, pp. 1-238.
Fujita, S.: 1991, Symmetry and combinatorial enumeration in chemistry, Berlin: Springer, pp. 1-368.
Gugisch, R.; Kerber, A.; Laue, R.; Meringer, M. & Weidinger, J.: 2000, ‘MOLFEN-COMB, a software package for combinatorial chemistry’, MATCH Communications in Mathematical and in Computer Chemistry, 41, 189-203.
Hässelbarth, W.: 1985, ‘On the inter-relation between orbits and double cosets’, Theoretica Chimica Acta, 67, 427-37.
Kerber, A.: 1999, Applied finite group actions, Berlin: Springer, pp. 1-454.
Kerber, A.: 2002, ‘Enumeration under finite group action, basic tools, results, and methods’, MATCH Communications in Mathematical and in Computer Chemistry, 46, 151-98.
Klein, D.J. & Cowley, A.H.: 1975, ‘Permutational isomerism’, Journal of the American Chemical Society, 97, 1633-40.
Klemperer, W.G.: 1972, ‘Enumeration of permutation isomerization reactions. II’, Inorganic Chemistry, 11, 2678-88.
Pólya, G.: 1937, ‘Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen’, Acta Mathematica, 68, 145-254.
Pólya, G. & Read, R.C.: 1987, Combinatorial enumeration of groups, graphs, and chemical compounds, New York: Springer, pp. 1-148.
Ruch, E. & Ugi, I.: 1969, ‘The stereochemical analogy model – A mathematical theory of dynamic stereochmistry’, Topics Stereochemistry, 4, 99-125.
Ruch, E.; Hässelbarth, W.; Richter, B.: 1970, ‘Doppelnebenklassen als Klassenbegriff und Nomenklaturprinzip fur Isomere und Ihre Abzahlung’, Theoretica Chimica Acta, 19, 288-300.
20. Physical organic theory
Baskin, I.I.; Skvortsova, M.I.; Stankevich, I.V. & Zefirov, N.S.: 1994, ‘Basis of invariants of labeled molecular graphs’, Doklady Chemistry, 359, 346-50.
Benson, S.W.: 1976, Thermochemical kinetics, New York: Wiley, pp. 1-336.
Bhatnagar, S.S. & Mathur, K.M.: 1935, Physical principles and applications of magnetochemistry, London: MacMillan, pp. 1-375.
Blaive, B. & Ziegler, J.C.: 2001, ‘Modeling of substituent effects: self-parameterization, a case of interdependence of the coefficients, illustrated on the linear plus cross-term models’, Journal of Mathematical Chemistry, 30, 69-81.
Cohen, N. & Benson, S.W.: 1993, ‘Estimation of heats of formation of organic compounds by additivity methods’, Chemical Reviews, 93, 2419-38.
Cox, J.D. & Pilcher, G.: 1970, Thermochemistry of organic and organometallic compounds, New York: Academic Press, pp. 1-643.
Essam, J.W.; Kennedy, J.W.; Gordon, M. & Whittle, P.:1977, ‘The graph-like state of matter.8.’, Journal of the Chemical Society, Faraday Transaction II, 73, 1289-307.
Fliszár, S.: 1983, Charge distributions and chemical effects: A new approach to the electronic structure and energy of molecules, Berlin: Springer, pp. 1-205.
Gordon, M. & Kennedy, J.W.:1973, ‘The graph-like state of matter. Part 2 – LCGI Schemes for the thermodynamics of alkanes and the theory of inductive inference’, Journal of the Chemical Society, Faraday Transaction II, 69, 484-504.
Hammett, L.P.: 1937, ‘The effect of structure upon the reactions of organic compounds. Benzene derivatives’, Journal of the American Chemical Society, 59, 96-103.
Hansch, C.; Leo, A. & Taft, R.W.: 1991, ‘A survey of Hammett substituent constants and resonance and field parameters’, Chemical Reviews, 91, 165-95.
Hässelbarth, W.: 1994, ‘Cluster-of-variables decomposition, a new mathematical tool for analysing structure-property relations’, MATCH Communications in Mathematical and in Computer Chemistry, 31, 7-21.
Jaffe, H.H.: 1953, ‘A reexamination of the Hammett equation’, Chemical Reviews, 53, 191-261.
Janz, G.J.: 1955, ‘The estimation of thermodynamic properties for organic compounds and chemical reactions’, Quarterly Reviews, 9, 229-54.
Kamlet, R.J. & Taft, R.W.: 1985, ‘Linear solvation energy relationships. Local empirical rules – or fundamental laws of chemistry? A reply to the chemometricians’, Acta Chemica Scandinavica, 39, 611-28.
Kennedy, J.W. & Gordon, M.: 1979, ‘Graph contractions and a generalized Möbius inversion’, Annals of the New York Academy of Sciences, 319, 331-8.
Klein, D.J.: 1986, ‘Chemical graph-theoretic cluster expansions’, International Journal of Quantum Chemistry, 20, 153-71.
Klein, D.J.; Schmalz, T.G. & Bytautas, L.: 1999, ‘A chemical sub-structural cluster expansions for molecular properties’, SAR & QSAR Environmental Research, 10, 131-56.
Leroy, G.: 1985, ‘Theoreical approach to some chemical problems’, Advances in Quantum Chemistry, 17, 1-95.
Lyman, W.J.; Reehl, W.F. & Rosenblatt, D.H.: 1982, Handbook of chemical property estimation methods, New York: McGraw-Hill, pp. 1-977.
Nguyen, T.H.; Goss, K.U. & Ball, W.P.: 2005, ‘Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments’, Environmental Science and Technology, 39, 913-24.
Parks, G.S. & Huffman, H.M.: 1932, The free energies of some organic compounds, New York: Chemical Catalog Company, pp. 1-251.
Pedley, J.B.; Naylor, R.D. & Kirby, S.P.: 1986, Thermochemical data of organic compounds, London: Chapman & Hall, pp. 1-792.
Rossini, F.D.; Pitzer, K.S.; Arnett, R.L.; Braun, R.M. & Pimentel, G.C.:1953, Selected values of physical and thermodynamic properties of hydrocarbons and related compounds, Pittsburgh: Carnegie Press, pp. 1-1050.
Shorter, J.: 1982, Correlation analysis of organic reactivity with particular reference to multiple regression, Chichester: Research Studies Press, pp. 1-248.
Skvortsova, M.I.; Baskin, I.I.; Slovokhotova, O.L. & Zefirov, N.S.: 1994, ‘Methodology of constructing a general model for the structure-property relationship at the topological level’, Doklady Chemistry, 336, 496-9.
Smiles, S.: 1919, The relations between chemical constitution and some physical properties, London: Longmans & Green, pp. 1-234.
Smolenski, E.A.: 1964, ‘Application of the theory of graphs to calculations of the additive structural properties of hydrocarbons’, Russian Journal of Physical Chemistry, 38, 700-2.
Tateavskii, V.M.; Benderskii, V.A. & Yarovoi, S.S.: 1961, Rules and methods for calculating the physico-chemical properties of paraffinic hydrocarbons, Oxford: Pergamon, pp. 1-128.
Wells, P.R.: 1963, ‘Linear free energy relationships’, Chemical Reviews, 63, 171-219.
21. Chemical classification
Brønsted, J.N.: 1923, ‘The conception of acids and bases’, Recueil des Travaux Chimiques des Pays-Bas et de la Belgique, 42, 718-28.
Jensen, B.B.: 2002, Mendeleev on the periodic law: selected writings, 1869 – 1905, New York: Dover, pp. 1-320.
Klein, D.J.: 1995, ‘Similarity and dissimilarity in posets’, Journal of Mathematical Chemistry, 18, 321-48.
Klein, D.J. & Babic, D.: 1997, ‘Partial orderings in chemistry’, Journal Chemical Information and Computation Sciences, 37, 656-71.
Leal, W.; Restrepo, G. & Bernal, A.: 2012, ‘A network study of chemical elements: from binary compounds to chemical trends’, MATCH Communications in Mathematical and in Computer Chemistry, 68, 417-42.
Leigh, G.H.: 1990, IUPAC nomenclature of inorganic chemistry, London: Blackwell.
Lewis, G.N.: 1923, Valence and the structure of atoms and molecules, New York: Chemical Catalog Co. pp. 1-172.
Lewis, G.N.: 1938, ‘Acids and bases’, Journal of the Franklin Institute, 226, 293-13.
Metanomski, W.V.: 1991, IUPAC compendium of macromolecular nomenclature, Oxford: Blackwell.
Panico, R.; Powell, W.H. & Richer, J.C.: 1993, IUPAC nomenclature of organic compounds, London: Blackwell, pp. 1-208.
Randić, M.: 2003, ‘Aromaticity of conjugated polycyclic hydrocarbons’, Chemical Reviews, 103, 3449-605.
Usanovich, M.: 1939, Zhurnal Obschei Khimii, 9, 182.
22. Chemo-metrics & QSAR
Bennett, C.A. & Franklin, N.L.: 1954, Statistical analysis in chemistry and chemical industry, New York: Wiley.
Brereton, R.G.: 2003, Chemometrics: Data analysis for the laboratory and chemical plant, New York: Wiley, pp. 1-504.
Devillers, J. & Balaban, A.T.: 1999, Topological indices and related descriptors in QSAR and QSPR, New York: Gordon & Breach, pp. 1-811.
Hansch, C. & Albert, L.: 1995, Exploring QSAR, Volume 1: Fundamentals and applications in chemistry and biology, Washington DC: ACS, pp. 1-580.
Jurs, P.C. & Isenhour, T.L.: 1975, Chemical applications of pattern recognition, New York: Wiley, pp. 1-184.
Karelson, M.: 2000, Molecular descriptors in QSAR/QSPR, New York: Wiley, pp. 1-448.
Kier, L.B. & Hall, L.H.: 1976, Molecular Connectivity in Chemistry and Drug Research, New York: Academic Press, pp. 1-257.
Kier, L.B. & Hall, L.H.: 1986, Molecular connectivity in structure-activity analysis, New York: Wiley, pp. 1-262.
Randić, M.: 1991, ‘Resolution of ambiguities in structure-property studies by use of orthogonal descriptors’, Journal Chemical Information and Computer Sciences, 31, 311-20.
Richards, W.G.: 1977, Quantum pharmacology, London: ButterworthsLondon, pp. 1-273.
Todeschini, R. & Consonni, V.: 2000, Handboook of molecular descriptors, New York: Wiley, pp. 195-7.
23. Molecular biology
Armstrong, C.M. & Bezanilla, F.M.: 1973, ‘Current related to the movement of the gating particles of the sodium channels’, Nature, 242, 459-61.
Arratia, R.; Bollobás, B.; Coppersmith, D. & Sorkin, G.B.: 2000, ‘Euler circuits and DNA sequencing by hybridization’, Discrete Applied Mathematics, 104, 63-96.
Betancourt, M.R. & Onuchic, J.N.: 1995, ‘Kinetics of proteinlike models: The energy landscape factors that determine folding’, Journal Chemical and Physics, 103 , 773-87.
Brynegeloson, J.D.; Onuchic, J.N.; Socci, N. & Wolynes, P.G.: 1995, ‘Funnels, pathways, and the energy landscape of protein folding: A synthesis’, Proteins: Structure, Function and Genetics, 21, 167-95.
Chan, H.S. & Dill, K.A.: 1994, ‘Transition states and folding dynamics of proteins and heteropolymers’, Journal Chemical and Physics, 100, 9238-57.
Chance, B.: 1943, ‘The kinetics of the enzyme-substrate compound of peroxidase’, The Journal of Biological Chemistry, 151, 553-7.
Changeux, J.P. & Konishi, M.: 1987, The neural and molecular basis of learning, England: Ellis Horwood.
Cole, K.S.: 1962, ‘The advance of electrical models for cells and axons’, Biophysics Journal, 2, 101-19.
Delbrück, M.: 1985, Mind from Matter?, London: Blackwell, pp. 1-302.
Dickerson, R.E.; Timkovich, R.E.R. & Almassy, R.J.: 1976, ‘The cytochrome fold and the evolution of bacterial energy metabolism’, Journal of Molecular Biology, 100, 473-91.
Dill, K.A.: 1990, ‘Combinant forces in protein folding’, Biochemistry, 29, 7133-55.
Dove, W.F. & Davidson, N.: 1962, ‘Cation effects on the denaturation of DNA’, Journal of Molecular Biology, 5, 195-208.
Eigen, M.; Winkler, R. & Dress, A.: 1988, ‘Statistical geometry in sequence space: A method of quantitative comparative sequence analysis’, Proceedings of the National Academy of Sciences of the United States of America, 85, 5913-7.
Frauenfelder, H.; Sligar, S.G. & Wolynes, P.G.: 1991, ‘the energy landscapes and motions of proteins’, Science, 254, 1598-603.
Galzitskaya, O.V. & Finkelstein, A.V.: 1999, ‘A theoretical search for folding/unfolding nuclei in three-dimensional protein structures’, Proceedings of the National Academy of Sciences of the United States of America, 96, 11299-304.
Hodgkin, A.L. & Katz, B.: 1949, ‘The effect of sodium ions on the electrical activity of the great axon of the squid’, The Journal of Physiology, 108, 37-77.
Hodgkin, A.L.: 1975, ‘The optimum density of sodium channels in an unmylinated nerve’, Philosophical Transaction of the Royal Society, 270, 297-300.
Holste, D.; Grosse, I.; Buldyrev, S.V.; Stanley, H.E. & Herzel, H.: 2000, ‘Optimization of coding potentials using positional dependence of nucleotide frequencies’, Journal of Theoretical Biology, 206, 525-37.
Howell, J.A.; Smith, T.F. & Waterman, M.S.: 1980, ‘Computation of generating functions for biological molecules’, SIAM Journal on Applied Mathematics, 39, 119-33.
Hull, D.E.: 1960, ‘Thermodynamics and kinetics of spontaneous generation’, Nature, 1986, 693-4.
Kauzmann, W.: 1959, ‘Some factors in the interpretation of protein denaturation’, Advances in Protein Chemistry, 14, 1-63.
Kruskal, J.B.: 1983, ‘An overview of sequence comparison: Time warps, string edits, and macromolecules’, SIAM Review, 25, 201-33.
Kuhn, H.: 1972, ‘Self-organization of molecular systems and the evolution of the genetic apparatus’, Angewandte Chemie International Edition, 11, 798-820.
Li, J. & Scheraga, H.A.: 1984, ‘Real-space renormalization group treatment of the helix-coil transition in a homoplyamino acid chain’, Journal of Physical Chemistry, 99, 6580-6.
Maiorov, V.N. & Crippen, G.M.: 1992, ‘Contact potential that recognizes the correct folding of globular proteins’, Journal of Molecular Biology, 227, 876-88.
Miller, S. & Orgel, L.: 1974, The origins of life on earth, New Jersey: Prentice-Hall.
Mirsky, A.E. & Pauling, L.: 1936, ‘On the structure of native, denatured, and coagulated proteins’, Proceedings of the National Academy of Sciences of the United States of America, 22, 439-47.
Munson, P.J. & Robard, D.: 1980, ‘LIGAND: A versatile computerized approach for the characterization of ligand-binding systems’, Analytical Biochemistry, 107, 220-39.
Nemethy, G. & Scheraga, H.A.: 1962, ‘The structure of water and hydrophobic bonding in proteins. III. The thermodynamic properties of hydrophobic bonds in proteins’, The Journal of Physical Chemistry, 66, 1773-89.
Oparin, A.I.: 1957, The origin of life on the earth, New York: Academic Press, pp. 1-691.
Pauling, L. & Delbrück, M.: 1940a, ‘The nature of the intermolecular forces operative in biological processes’, Science, 92, 77-9.
Pauling, L.: 1940b, ‘A theory of the structure and process of formation of antibodies’, Journal of the American Chemical Society, 62, 2643-57.
Pauling, L.; Corey, R.B. & Branson, H.R.: 1951, ‘The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain’, Proceedings of the National Academy of Sciences of the United States of America, 37, 205-11.
Pauling, L.; Itano, H.A.; Singer, S.J. & Wells, I.C.: 1949, ‘Sickle-cell anemia, a molecular disease’, Science, 110, 543-8.
Perutz, M.F.: 1963, ‘X-ray analysis of hemoglobin’, Science, 140, 863-9.
Poland, D.; Vournakis, J.N. & Scheraga, H.A.: 1966, ‘Cooperative interactions in single-strand oligomers of adenylic acids’, Biopolymers, 4, 223-35.
Rackovsky, S. & Scheraga, H.A.: 1984, ‘Differential geometry and protein folding’, Accounts of Chemical Research, 17, 17-24.
Rich, A. & Davidson, N.: 1968, Structural chemistry and molecular biology, San Francisco: ed. W. H. Freeman Press, pp. 1-907.
Schrödinger, E.: 1945, What is life?, New York: MacMillan, pp. 1-194.
Teorell, T.: 1953, ‘Transport process and electrical phenomena in ionic membrames’, Progress in biophysics and biophysical chemistry, 3, 305-69.
Timoféeff-Ressovsky, N.V.; Zimmer, K.G. & Delbrück, M.: 1935, ‘Über die Natur der Genmutation und der Genstruktur’, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, mathematisch-physikalische Klasse, Fachgruppe VI: Biologie, 1, 189-45.
Turing, A.M.: 1952, ‘The chemical basis of morphogenesis’, Philosophical Transactions of the Royal Society, 237, 37-72.
Watson, J.D. & Crick, F.H.C.: 1953, ‘A Structure for desoxyribose nucleic acids’, Nature, 171, 737-8.
Welland, G.A. & Molinoff, P.B.: 1981, ‘Quantitative analysis of drug-receptor interactions. I. Determination of kinetic and equilibrium properties’, Life Sciences, 29, 313-30.
Wicken, J.: 1981, ‘Evolutionary self-organization and the entropy principle’, Nature and System, 3, 303-22.
Yue, K. & Dill, K. A.: 1993, ‘Sequence-structure relationships in proteins and copolymers’, Physical Review E, 48, 2267-78.
Zhu, H.Y. & Braun, W.: 1999, ‘Sequence specificity, statistical potentials, and three-dimensional structure prediction with self-correcting distance geometry calculations of -sheet formation in proteins’, Protein Science, 8, 326-42.
Zwanzig, R.: 1997, ‘Two-state models of protein folding kinetics’, Proceedings of the National Academy of Sciences of the United States of America, 94, 148-50.
Zwolinski, B.J.; Eyring, H. & Reese, C.E.: 1949, ‘Diffusion and rate theory in protein synthesis’, Archives of Biochemistry and Biophysics, 1, 52-62.
24. Chemo-informatics
Cammann, K. & Vögtle, F.: 1985, Biomimetic and bioorganic chemistry, New York: Springer, pp. 1-259.
Dolphin, D.; McKenna, C.; Murakami, Y.; Tabushi, I.: 1980, Biomimetic chemistry, Washington DC: ACS, pp. 1-437.
Fort, G. & Lambert S.: 2005, ‘Classification using partial least squares with penalized logistic regression’, Bioinformatics, 21, 1104-11.
Gasteiger, J. & Engel, T.: 2003, Chemoinformatics, New York: Wiley-VCH, pp. 1-680.
Gordon, E.M. & Kerwin, J.F.: 1988, Combinatorial chemistry and molecular diversity in drug discovery, New York: Wiley, pp. 1-544.
Gruber, D.B.: 2000, ‘MCR XVI. Mathematical support for combinatorial chemistry’, Journal of Chemical Information and Computation Sciences, 40, 580-7.
Hanko, R. & Hartwig, W.: 2002, Handbook of combinatorial chemistry, New York: Wiley-VCH, pp. 10-23.
Illet, P.: 1989, Similarity and clustering in chemical information systems, England: Wiley, pp. 1-266.
Jenkins, J.L.; Glick, M. & Davies, J.W.: 2004, ‘A 3D similarity method for scaffold hopping from known drugs or natural ligands to new chemotypes’, Journal of Medicinal Chemistry, 47, 6144-59.
Johnson, M.A. & Maggiora, G.M.: 1990, Concepts and applications of molecular similarity, New York: Wiley, pp. 1-393.
Kuchanov, S.; Pizik, I. & Ivanov, V.: 2004, ‘Theoretical consideration of the grafting of polymer chains onto fullerene C60’, Macromolecular Theory and Simulations, 13, 230-40.
Likhtenshtein, G.I.: 2003, New trends in enzyme catalysis and biomimetic chemical reactions, Boston: Kluwer, pp. 1-230.
Mann, S.: 1995, Biomimetic materials chemistry, Berlin: VCH, pp. 1-400.
Monev, V.: 2004, ‘Introduction to similarity searching in chemistry’, MATCH Communications in Mathematical and in Computer Chemistry, 51, 7-38.
Taguchi, Y.H. & Oono, Y.: 2005, ‘Nonmetric multidimensional scaling as a data-mining tool: new algorithm and new targets’, Advance in Chemical Physics, 130-B, 315-51.
Toldo, L. & Rippmann, F.: 2005, ‘Integrated bioinformatics application to automated target discovery’, Journal of the American Society for Information Science and Technology, 56, 483-92.
25. Chemical graph theory
Aihara, J.; Babic, D. & Gutman, I.: 1996, ‘Matching spectra of fullerenes’, MATCH Communications in Mathematical and in Computer Chemistry, 33, 7-16.
Babic, D.; Brinkmann, G. & Dress, A.: 1997, ‘Topological resonance energy of fullerenes’, Journal of Chemical Information and Computer Sciences, 37, 920-3.
Brinkmann, G. & Dress, A.W.M.: 1997, ‘A constructive enumeration of fullerenes’, Journal of Algorithms, 23, 345-58.
Brinkmann, G. & Dress, A.W.M.:1998, ‘A reliable and efficient top-down approach to fullerene-structure enumeration’, The Advances in Applied Mathematics and Mechanics, 21, 473-80.
Brinkmann, G. & Greinas, J.: 2003, ‘Pentagon-hexagon patches with short boundaries’, European Journal of Combinatorics, 24, 517-29.
Brinkmann, G. & Fowler, P.W.: 2003, ‘A catalogue of growth transformations of fullerene polyhedra’, Journal of Chemical Information and Computer Sciences, 43, 1837-43.
Brinkmann, G.; Fowler, P.W. & Justus, C.: 2003, ‘A catalogue of isomerization transformations of fullerene polyhedra’, Journal of Chemical Information and Computer Sciences, 43, 917-27.
Došlić, T.: 1998 ‘On lower bounds of number of perfect matchings in fullerene graphs’, Journal of Mathematical Chemistry, 24, 359-64.
Došlić, T.: 2002a, ‘On some structural properties of fullerene graphs’, Journal of Mathematical Chemistry, 31, 187-95.
Došlić, T.: 2002b, ‘On lower bounds on the number of perfect matchings in n-extendable bricks’, The Australasian Journal of Combinatorics, 26, 193-8.
Fowler, P.W.: 1986, ‘How unusual is C60? Magic numbers for carbon clusters’, Chemical Physics Letters, 131, 444-50.
Herndon, W.C.: 1974, ‘Thermochemical parameters for benzenoid hydrocarbons’, Thermochimica Acta, 8, 225-37.
Klein, D.J. & Liu, X.: 1991, ‘Many-body conjugated-circuit computations’, Journal of Computational Chemistry, 12, 1260-4.
Klein, D.J. & Liu, X.: 1992, ‘Theorems for carbon cages’, Journal of Mathematical Chemistry, 11, 199-205.
Klein, D.J.; Seitz, W.A. & Schmalz, T.G.: 1990, ‘Conjugated-circuit computations for conjugated hydrocarbons’ in: D.H. Rouvray (ed.), Computational chemical graph theory, New York: Nova Sciences Publisher, pp. 128-47.
Kroto, H.W.: 1987, ‘The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60, & 70’, Nature, 329, 529-32.
Manolopolous, D.E. & Fowler, P.W.: 1992, ‘Molecular graphs, point groups, and fullerenes’, Journal of Chemical Physics, 96, 7603-14.
Randić, M.: 1977a, ‘A graph theoretical approach to conjugation and resonance energies of hydrocarbons’, Tetrahedron, 33, 1905-20.
Randić, M.: 1977b, ‘Aromaticity and conjugation’, Journal of the American Chemical Society, 99, 444-50.
Sah, C.H.: 1993, ‘Combinatorial construction of fullerene structures’, Croatica Chemica Acta, 66, 1-12.
Schmalz, T.G.; Seitz, W.A.; Klein, D.J. & Hite, D.J.: 1988, ‘Elemental carbon cages’, Journal of the American Chemical Society, 110, 1113-27.
Trinajstić, N.: 1992, Chemical graph theory, Florida: CRC Press, p. 303.
Zhang, H. & Zhang, F.: 2002, ‘New lower bound on the number of perfect matchings in fullerene graphs’, Journal of Mathematical Chemistry, 30, 343-7.
Douglas J. Klein:
Texas A&M University at Galveston, Galveston, Texas 77553-1675, USA; kleind@tamug.edu
Copyright © 2013 by HYLE and Douglas J. Klein
|