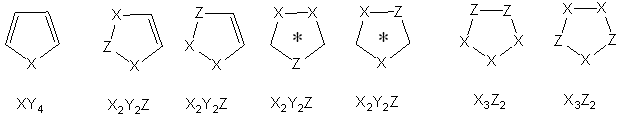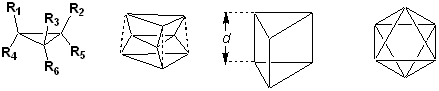Chemical Graph Theory and the Sherlock Holmes Principle

  

Abstract: The development of chemical applications of graph theory is reviewed from a personal perspective. Graph-theoretical methods for finding all graphs fulfilling certain mathematical conditions followed by eliminating chemically impossible solutions are equivalent to the ‘Sherlock Holmes principle’. For molecular graphs, this is illustrated by monocyclic aromatic systems and by valence isomers of annulenes. Using dualist graphs for benzenoids and diamond hydrocarbons it was possible to develop simple encoding systems that allowed convenient enumerations of isomers. Starting with the invention of reaction graphs in 1966 that included the Petersen graph which is also the 5-cage (the smallest graph with girth 5) two gaps were filled by discovering the first 10-cage and the unique 11-cage, showing how chemical clues can lead to interesting mathematical developments. Graphs of a third type are represented by synthon graphs that are helping chemical synthesis. Connections between chemical structure and molecular properties allow the design of biologically active substances on the basis of quantitative structure-activity relationships (QSARs). Some of the simplest tools for QSAR are topological indices and they are briefly discussed.

Keywords: mathematical chemistry, molecular graphs, reaction graphs, synthon graphs, topological indices, QSAR.

 

1. Introduction

This article presents a personal account of the author’s research activity centered on chemical applications of graph theory including an overview of the interactions between chemistry and discrete mathematics. A few previous retrospective essays have been published earlier (Balaban 1993a, 1995, 2000b, 2005, 2011a, 2012a,b).

During my high school years, I was equally fascinated by experiments with chemicals in my ‘amateur-chemist’ home-laboratory and by trying to find solutions to mathematical problems, of course at elementary levels in both cases. Thus I devised formulas for solid angles of regular and semiregular polyhedra, for which I had built cardboard models, and I published these data about 60 years later (Balaban & Bonchev 2005, Vukičević & Balaban 2008). In 1949 I decided to become a chemist rather than a mathematician, and after graduating as a chemical engineer in 1953, I was enrolled as a Ph. D. student with the best organic chemistry professor in Romania, Costin D. Nenitzescu. After six years I defended my thesis and the results were described in two chapters of Olah’s multi-volume monograph Friedel-Crafts and Related Reactions (Balaban & Nenitzescu 1964, Nenitzescu & Balaban 1964). Organic chemical reactions which have come to be recognized and referred to by name within the chemistry community are known as Organic Name Reactions; Nenitzescu’s name is associated with two such name reactions (indole syntheses). One of the discoveries I made during my Ph. D. work, which is now known as the Balaban-Nenitzescu-Praill reaction (Hassner & Stumer 2002, Balaban 2011b) was a new synthesis of pyrylium salts (these are benzene analogs with a positively-charged oxygen heteroatom replacing a CH group of benzene). Together with my ‘doctor-father’ Nenitzescu, I published many papers on syntheses of various pyrylium salts and their reactions. After Nenitzescu passed away in 1970, I continued to study conversions of pyrylium salts into other aromatic systems, and published several reviews on pyrylium salts (Balaban et al. 1982, Balaban & Balaban 2003). The preceding review was written with my son, Teodor-Silviu Balaban, who is a professor of chemistry at the University of Marseille. In Roumania after 1970 experimental research became more and more difficult, and I gradually started to lean towards theoretical studies.

Looking back now at the theoretical part of my research activity that started soon afterwards, I realized that (like many organic chemists) I was imitating a character in Molière’s play Le Bourgeois Gentilhomme who was speaking in prose without realizing it. More precisely, in writing organic chemical formulas and figuring out all constitutional isomers, chemists made unconscious use of graph theory. Realizing that a chemist needs to use consciously graph theory, I tried to become familiar with the ‘chemical versus graph-theoretical vocabulary’ (see Table 1). Articles by Dennis Rouvray also helped (Rouvray 1971, 1974). In what follows I will review some aspects of mathematical chemistry from a very personal view point.

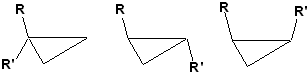
In chemistry, constitutional isomers are substances with the same molecular formula, i. e. composed from the same kinds of atoms bonded differently, such as butane and isobutane C₄H₁₀: the former has a linear chain of carbon atoms, and the latter a branched chain (each carbon atom is tetravalent and is symbolized by a vertex of degree 4 in the graph where all C and H atoms are displayed; usually, however, organic chemists use hydrogen-depleted graphs). When rings or double bonds are present, diastereoisomers with the same constitution (connectivity) but with different geometry may result; and when three-dimensional structures are taken into account, enantiomers result for instance when a tetravalent carbon atom is connected to four different substituents, and such a molecule is not superimposable on its mirror image. As an example, let us examine disubstituted cyclopropanes shown in Fig. 1, where R and R’ are monovalent substituents such as halogen atoms or alkyl groups like methyl, ethyl. 1,1-Disubstituted cyclopropane (1) has a different connectivity than 1,2-disubstituted cyclopropanes 2 and 3, hence 1 is a constitutional isomer of 2 and 3. On the other hand, 2 (trans) and 3 (cis) are stereoisomers. If R = R’ then 3 has an internal plane of symmetry, hence it is achiral and cannot be split into two enantiomers, but it can if R ≠ R’. However, 2 is always achiral, irrespectively whether R = R’ or R ≠ R’, because such molecules are not superimposable on their mirror images.

Valence isomers form a special class of constitutional isomers and they conserve atomic partitions but differ in the distribution of shared electrons; examples are valence isomers of annulenes (CH)_2k, to be discussed in a separate section, or of adamantane (CH₂)₆(CH)₄.

2. The Sherlock Holmes Principle and constitutional formulas of all isomers

In several of Conan Doyle’s stories, Sherlock Holmes identifies the felon by using the following principle: When you have eliminated the impossible, whatever remains, no matter how improbable, must contain the truth. This principle can be applied profitably to chemical problems by considering all possibilities and then systematically eliminating the impossible. For organic-chemical problems involving molecules (i.e. aggregates of atoms symbolized by graph vertices connected by covalent bonds symbolized by graph edges), graph theory is the tool for dealing with the first part, namely the enumeration of all possibilities. Subsequently, chemical restrictions and other considerations will have to be used for solving the problem.

One of my ambitious goals at the beginning was finding all possible aromatic compounds that fulfill the famous Hückel Rule (aromatic rings must have 4n + 2 π-electrons) when a ring of m atoms has continuous conjugation. Restricting the choice of atoms to elements in the same period from boron to oxygen as well as the global charges to +1, 0, and −1, and reasoning that according to the Pauli Principle a molecular orbital can host at most two π-electrons, there are three and only three types of atoms that may form an aromatic ring, namely with 2, 1, and 0 π-electrons, denoted by X, Y, and Z, respectively, so that the formula of this ring is X_xY_yZ_z and the coefficients x, y, and z must satisfy a pair of Diophantine equations for given m and n values:

Fig. 2 presents the three types of atoms with the above restrictions. It is easy to see that there are many solutions for this problem, and that for some solutions one has to solve a graph-theoretical problem known as ‘the necklace problem’ for three bead colors (see below).

Thus, for five-membered rings (m = 5) with π-electron sextet (n = 1), there are three solutions presented in Fig. 3: the unique XY₄ molecule, the four X₂Y₂Z necklaces, and the pair of X₃Z₂ necklaces. In this text Y-type atoms (which may be neutral or electrically charged) are not shown explicitly.

When considering heterocycles with more than one Z-type heteroatom, the number of possible isomers increases tremendously. In order to cut down these numbers one may consider only systems with no adjacent Z-type atoms, and one may also exclude molecules that have sequences of odd numbers of Y-type atoms (mesoionic molecules). Most of such systems have little chance of leading to stable aromatics. This reasoning was continued when I tried to obtain experimentally new boron-containing heteroaromatics such as boroxaro-pyrylium salts (Balaban et al. 1964a, 1964b, 1970a).

In 1959, when I obtained my Ph. D. degree and embarked on an academic pathway at the Bucharest Polytechnic, where Nenitzescu was the Head of the Organic Chemistry Department, I published in Romanian this systematic approach to enumerating all possible monocyclic aromatic compounds (Balaban 1959). By devising for each atom type in Figure 2 an ‘aromaticity constant’ based on electronegativities relatively to CH groups and summing all such constants for the complete ring, it was possible to establish an approximate range for stabilities. Thus one obtains –100 for cyclopentadienyl anion, 0 for benzene, +100 for tropylium ion. For substituents R ≠ H an approximate relationship based on Hammett constants was devised (Balaban & Simon 1962). Three recent reviews about aromaticity of heterocycles mention this XYZ approach (Balaban et al. 2004; Balaban 2009a, 2010).

With the help of my lifelong mathematician friend, Silviu Teleman, the necklace problem was solved by an elaborate formula (I learned later that it was similar, but not identical to Redfield’s approach). The simplest solution would have been via Polya’s Theorem that was using the molecular symmetry (rotations around proper symmetry axes) to obtain the cycle index Z(G) of the graph G and from it the isomer-counting series ICS(G), as shown in the next section.

3. Valence isomers of annulenes (CH)_2k

The next problem I turned my attention to involved valence isomers of [n]annulenes. In Bucharest, the first of such isomers of (CH)₁₀ had been prepared (Avram et al. 1957), and Doering called it the Nenitzescu hydrocarbon (Doering & Rosenthal 1966). I realized (Balaban 1966) that this is equivalent to enumerating all possible cubic multigraphs (i.e. regular graphs of valence three, in which each vertex has degree 3, allowing multiple bonds). By eliminating the non-planar graphs, impossible to correspond to chemical compounds, one can then consider separately planar graphs containing only single bonds ( -electrons) and planar multigraphs that have also double bonds (π-electrons). Till then, the valence isomers of benzene, (CH)₆, which were being sought after experimentally, did not include bis-cyclopropenyl, but it became clear that my graph-theoretical enumeration (which was based on general graphs where loops and multiple bonds were allowed) resulted in six cubic multigraphs. One of these was the non-planar twisted triprismane that can be considered to be a ‘benz-moebius-stripane’, which is not an isolable molecule. Eventually, all five unsubstituted (Fig. 4) and substituted valence isomers of benzene were obtained in various laboratories. Even more fruitful were my enumerations of valence isomers of [10]annulene, [12]annulene, and [14]annulene, most of which have still to be synthesized. All results were later grouped in a 3-volume monograph (Balaban et al. 1986).

An interesting fact, with historical connotations, is that the cycle indices for constitutional isomers of Kekulé’s benzene (4) and Ladenburg’s benzprismane formulas (7) are identical, and as a consequence the numbers of di- and trisubstituted isomeric derivatives are identical, as will be presented in detail below. When Kekulé presented his formula for benzene, which had been discovered by Faraday four decades earlier, there was a controversy between Kekulé and Ladenburg based on these numbers of isomers. Nowadays one knows that the Ladenburg benzprismane formula has considerable steric strain and that it generates also enantiomers as discussed in Balaban 1974.

4. Polya’s theorem as the best tool for isomer counting

Although the solution of the necklace problem published in 1959 did not make use of the Polya Theorem, later I learnt how to employ it. As an example, for counting isomers of substituted cyclopropanes, consider Fig. 5, which provides more detail than Fig. 1.

The symmetry operations for a trigonal prism are expressed by the cycle index Z:

For counting all constitutional and stereo-isomers with two types of substituents R_i, say H and F, denoted by r and s, we convert the cycle index Z into the isomer counting series (ICS) by substituting into Z the ‘figure-counting series’:

and we obtain ICS = r⁶ + r⁵s + 4r²s² + 4r³s³ + …, meaning that when counting all possible isomers there are: one isomer for the unsubstituted and mono-fluoro-substituted, four difluoro-substituted cyclopropanes (namely 1,1-difluoro-, cis-1,2-difluoro-, R-trans-1,2-difluoro-, and S-trans-1,2-difluorocyclopropane – with the last two being enantiomers), four trifluorosubstituted isomers (namely R-1,1,2-trifluoro-, S-1,1,2-trifluoro-, all-cis-1,2,3-trifluoro-, and cis-trans-1,2,3-trifluorocyclopropane), etc.

Neglecting enantiomerism, we derive a new Z index by ignoring the third dimension, and we consider the symmetry of an infinitely-thin trigonal prism, with d = 0. Then we have

yielding by substitution (4) the isomer-counting series ICS = r⁶ + r⁵s + 3r²s² + 3r³s³ + …, meaning that the two R, S-enantiomers are now no longer counted separately, but the cis/trans isomers still count.

Finally, for counting only constitutional isomers and neglecting completely stereoisomers, we consider the last graph of Fig. 5 (flattened trigonal antiprism) for which the Z-index takes into account both proper and improper axes of rotation:

and by substitution (4) one obtains the isomer-counting series ICS = r⁶ + r⁵s + 2r²s² + 2r³s³ + …, meaning that one counts only the pair of 1,1-difluoro- and 1,2-difluorocyclopropane, or the pair of 1,1,2-trifluoro- and 1,2,3-trifluoro-cyclopropane as constitutional isomers.

The above example shows the original finding on how to use graphs for counting separately various types of isomers (Balaban 1978). A review on methods for isomer counting was published as a book chapter (Balaban 1991).

Cycle indices for the valence isomers of benzene are presented in Table 2. Two of these cycle indices have been examined above in equations (3) and (5). It may be seen that when one excludes stereoisomerism for benzprismane, its cycle index is identical to that of benzene (co-isomeric multigraphs). The complete documented story of the Kekulé-Ladenburg controversy, which ended by favoring the Kekulé structure due to Baeyer’s experiments, was described (Balaban 1974, Klein & Bytautas 2000). It would be interesting for chemistry students (who should be made aware of the bonds between chemistry and discrete mathematics including combinatorics, group theory, and graph theory) to learn how easy it is to enumerate all kinds of chemical isomers by using the powerful Polya Theorem.

5. Benzenoids: collaborating with Harary and Tomescu

Attempts to collaborate with Romanian graph-theorists were unsuccessful, but following Silviu Teleman’s advice, I got in contact by mail with Frank Harary who had authored the best-known book on the graph theory (Harary 1969). Shortly afterwards, Frank visited me in Bucharest and we started to collaborate first with applying Polya’s theorem to enumerating isomers (Balaban & Harary 1967), then with particular cases of enumerating graph-theoretically planar (CH)₁₀ isomers (Balaban et al. 1970b), drawing attention that characteristic polynomials do not characterize graphs up to isomorphism (Balaban & Harary 1971), and writing a chapter for the book entitled Chemical Applications of Graph Theory (Balaban & Harary 1976). I had started to edit this book in Bucharest in the mid-60s, but it took about 10 years till it was published in the summer of 1976 (with a preface written by Vlado Prelog, who was awarded the Nobel Prize at the end of 1976) after I returned from Vienna where I worked as Senior Research Scientist for three years at the International Atomic Energy Agency (there I was in charge with symposia and monographs on radioisotopes and radiopharmaceuticals).

A different type of collaboration with Harary involved polycyclic aromatic hydrocarbons also known as benzenoids. We published jointly a paper using the idea of dualists having the centers of benzenoid rings as vertices and pairs of vertices in rings sharing a CC bond as edges (Balaban & Harary 1968). These dualists are not actually normal graphs because angles between edges do matter for dualists, differentiating for instance anthracene (with a collinear dualist) from phenanthrene (with a kinked dualist). Thus we arrived at a graph-theoretical definition for cata-condensed benzenoids when the dualist by acyclic, for peri-fused benzenoids when the dualist has three-membered rings and possibly acylic branches, and finally for coronoids when the dualist has larger rings. In addition, catafusenes can be encoded by using digit 0 for straight-annelation along the sequence of benzenoid rings from one end of the longest chain of rings, and digits 1 and 2 for kinked annelation (keeping the same digit 1/2 for right/left annelation). Fig. 6 displays all possible polycyclic aromatic hydrocarbons with four benzenoid rings. The cata-condensed benzenoids have their notation in square brackets; the last benzenoid in Fig. 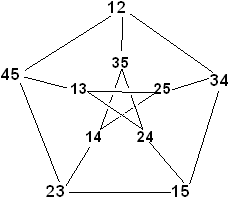6, without notation, is peri-condensed and is called pyrene.

The dualist approach for benzenoids was continued (Balaban 1969a) and reviewed (Balaban 1980b, 1982b), and later extended to three-dimensional diamondoid hydrocarbons as will be discussed further below. For benzenoids I devised a new terminology: by analogy with acenes that have straight chains of benzenoid rings (in Fig. 6 the first one is tetracene with notation [00]), fibonacenes are catafusenes encoded by a sequence of digits 1 and 2, e.g. the 3^rd and 4^th benzenoids in Fig. 6; the numbers of their Kekulé resonance structures are Fibonacci numbers (Balaban 1969b). A more recent review on fibonacenes is available (Gutman & Klavžar 2006).

In collaborations with the Romanian mathematician Ioan Tomescu from Bucharest, we published jointly about generalized Fibonacci numbers characterizing the numbers of Kekulé resonance structures for catafusenes that have straight chains of benzenoid rings alternating with kinks (Balaban & Tomescu 1985). Catafusenes with codes differing only by permutations between digits 1 and 2 (e.g. again the 3^rd and 4^th benzenoids in Fig. 6) share the same numbers of Kekulé resonance structures and are called isoarithmic (Balaban & Tomescu 1983) or isoresonant (Živković et al. 2000). Other mathematical problems connected with the number of resonance (Kekulé) structures of benzenoids were presented (Balaban & Tomescu 1984, 1988).

Polycyclic benzenoids can be defined either as portions of graphene or as benzenoid molecules sharing CC bonds; only in the latter case one should include helicenes, and because of this fact, isomer counts of polycyclic benzenoids differed among various authors. With the agreement of 14 authors working in this field, a consolidated report was published in 1987 (Balaban et al. 1987). Since then, powerful new computer programs for enumerating benzenoids have been developed (Brinkmann et al. 2003).

6. Reaction graphs

So far, the only types of chemical graphs that had been studied were molecular graphs. A different type of graphs became apparent when I tried to visualize all possible intermediates in the cationic 1,2-shift rearrangement of a penta-substituted ethylcarbenium cation with five different substituents. If the two ethyl carbon atoms were distinguishable (e.g. by labeling one of them with a carbon isotope) a nice symmetric cubic graph with 20 vertices resulted, representing each of these intermediates. When I learned that this graph, which some authors called ‘Balaban graph’ (Heller 1969, De Bruin et al. 1969), had been previously described as the Desargues-Levi graph (or Levi graph of the Desargues configuration), I wrote to all these authors asking for the correct name to be used henceforth. If the ethyl carbon atoms are equivalent (indistinguishable), the graph has only 10 vertices and is known as the Petersen graph or the cubic (trivalent) 5-cage, adorning the cover of Harary’s book on Graph Theory (Harary 1969). Together with two coworkers, I published these results on reaction graphs (Balaban et al. 1966) (one of them, Dan Farcasiu, emigrated to USA soon afterwards, and is now Professor Emeritus). Soon afterwards, the same reaction graphs appeared in two publications when examining the intermediates in the rearrangements of trigonal-bipyramidal pentasubstituted phosphoranes: the Desargues-Levi graph resulted when stereoisomerism was considered (Lauterbur & Ramirez 1968) and the Petersen graph resulted when only constitutional isomerism was taken into account (Dunitz & Prelog 1968). It was Mislow who pointed out the priority of my publication (Mislow 1970, Mislow & Zon 1971). As an explanation for the vertex notation in Figures 7 and 8, we discuss reaction graphs for 1,2-shifts of a pentasubstituted ethylcarbenium cation with five different substituents R¹ to R⁵ having one of the two ethyl carbon atoms labeled with ¹³C or ¹⁴C, and denoted by an asterisk (C*). Then we represent in Fig. 7 the cation R¹R²C⁺—C*R³R⁴R⁵ by the notation ‘.12’ and the isotopomeric cation R¹R²C⁺*—CR³R⁴R⁵ with the label at the cationic center by the notation ‘12.’. For the reaction graph of the turnstile rotation for a pentasubstituted phosphorane the same notation would distinguish the two enantiomers having equatorial substituents R¹ and R². In Fig. 8 one can see the Petersen graph for the same processes involving the unlabeled ethylcarbenium ion or the phosphorane without differentiating enantiomers, with vertex notations having no period (full stop) preceding or following the two substituent subscripts.

This area of reaction graphs continued to be developed, and provided other graphs with spectacular higher symmetry, as reviewed in a book chapter (Balaban 1994b). For Schleyer’s catalyzed cationic isomerizations yielding polymantanes, reaction graphs led to interesting perspectives (Whitlock & Siefken 1968, Engler et al. 1973). Also, this area led in 1978 to a collaboration with Schleyer that involved a generalization of dualist graphs to polymantanes (diamondoid hydrocarbons) (Balaban & Schleyer 1978). In 1976 I had published an encoding system for staggered alkane rotamers (Balaban 1976a, 1976b) and I realized that thus, by analogy with the 2-dimensional dualists of benzenoids, one can encode 3-dimensional diamondoids. Whereas for cata-condensed benzenoids the coding was based on three digits 1, 0, and 2 corresponding to dualist angles of 120º, 180º, and 240º, for diamondoids one uses digits 1, 2, 3, and 4 for tetrahedral bond orientations. R.M.K. Carlson, J.E. Dahl and coworkers reported about the isolation of many diamond hydrocarbons from petroleum in the Gulf of Mexico (Dahl et al. 2003). Recently, the encoding mentioned above served for correlations between structures and chromatographic data (gas-liquid and high-pressure liquid chromatography) of diamond hydrocarbons in a collaboration involving Carlson and Dahl as well as Klein (Balaban et al. 2007b).

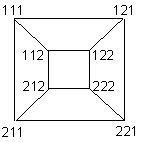
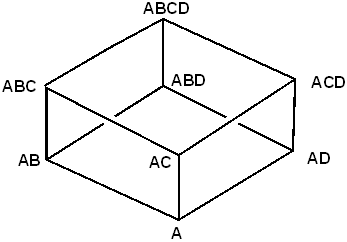
Recently, the partition of diamondoids according to the numbers of CH₂, CH, and C groups, taking also into account the dualists with their partitions according to vertices of degrees 1, 2, 3, and 4, revealed an interesting periodicity (Balaban 2012c, 2013a, 2013b).

7. Synthon graphs and various other chemical graphs

A third type of chemical graphs are the synthon graphs (Balaban 1980a) in which vertices symbolize molecules from multistep synthetic reactions, starting with a target molecule followed by retrosynthetic steps till simple starting materials are reached. This ‘disconnection approach’ to computerized synthetic chemistry has allowed spectacular syntheses of complicated molecular structures. The LHASA program (Logic and Heuristic Applied to Synthetic Analysis) was initiated (Corey & Wipke 1969) and was subsequently developed by Corey with spectacular results as detailed in a book (Corey & Cheng 1989) and Nobel Prize lecture (Corey 1990). For a synthesis to be successful and economical, many conditions must be fulfilled, and one of these is to be convergent (Hendrickson 1977).

For synthesizing an organic compound there are definite numbers of possibilities for connecting synthons. Thus, for connecting n = 4 synthons A, B, C, and D there are 8 possibilities: ABCD, ABC+D, AB+CD, A+BCD, AB+C+D, A+BC+D, A+B+CD, A+B+C+D, and the synthon graph is a cube graph. In Fig. 9, the left-hand cube vertices are labeled by three symbols from a binary set (in this case instead of 0 and 1, we have used 1 and 2). Two vertices are adjacent when they differ by exactly one digit. In general, one obtains an (n – 1)-cube for all possibilities of assembling a linear chain composed of n carbon atoms or n synthons.

In the book about pyrylium salts (Balaban et al. 1982) the synthon graph is represented by a hypercube because for assembling the five carbon atoms of the pyrylium cation, one needs a synthon graph with 2^5–1 = 16 vertices. In agreement with the Sherlock Principle, this hypercube is reduced by the realistic requirement that the 3-component syntheses should contain two identical moieties so as not to yield complicated mixtures. In Fig. 10, the thick lines symbolize C–C bonds, X symbolizes the O⁺ heteroatom, and the circles symbolize one-carbon moieties. The formation of pyrylium salts from 2-pentene-1,5-diones (pyrylium psdeudobases) or 2,4-pentadien-1-ones illustrates one-component synthesis; from the pair of two-component syntheses, the left-hand one represents the acylation of  , - or  , -unsaturated ketones, and the right-hand one illustrates the condensation of a propenone or a 1,3-diketone with a methyl(ene) ketone; and from the triplet of three-component syntheses, the left-hand one represents the diacylation of propenes (Balaban-Nenitzescu-Praill reaction), the middle one illustrates the dehydrogenating condensation between an acyl chloride with two moles of methyl(ene) ketone, and the right-hand one represents the reaction between an ortho-ester and two moles of methyl(ene) ketone. Thus, from all four-membered circuits of the hypercube, the realistic synthon graph from Fig. 10 conserves just one such circuit.

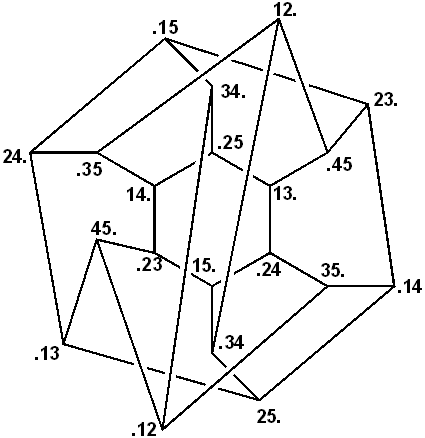
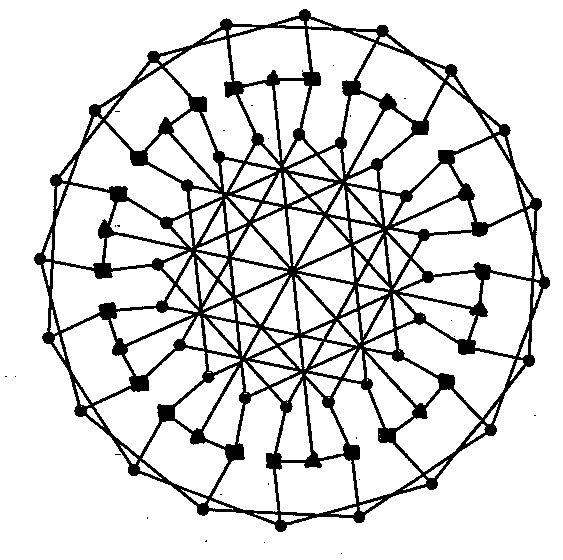
In several publications I discussed how graphs could represent chemical reactions (Balaban 1972b, Balaban & Kerek 1974). There exist other types of chemical graphs, for instance resonance graphs (Herndon 1974, Randić et al. 1996, Klavžar & Petra 2005), in which vertices symbolize Kekulé (resonance) structures. They are portions of hypercubes and are related to product graphs (Imrich & Klavžar 2000, Imrich et al. 2008). In the series of 54 papers that I published between 1966 and 1991 under the general title Chemical Graphs, I have discussed molecular graphs, reaction graphs, synthon graphs, benzenoids, and also topological indices, which will be discussed in the next section.

8. Topological indices

Chemical compounds are associated with physical and chemical properties, and some of these compounds have biological activities. Actually, in the search for new antibacterials and various other medicinal drugs, pharmaceutical companies synthesize and test annually millions of new compounds, characterizing in detail those compounds that show some promise. In 2011 the number of substances registered in the Chemical Abstracts Database reached 60 million. Testing for biological activity is expensive, therefore many theoretical methods have been devised for correlating structures with biological activities or physical-chemical properties. One of the simplest methods for quantitative structure-activity or structure-property relationships (QSAR and QSPR, respectively) involves molecular descriptors called topological indices (TIs). This name was introduced for the Z-index (Hosoya 1971). Since physical properties or bioactivities are expressed in numbers whereas chemical structures are discrete graphs, in order to associate graphs with numbers one has to rely on graph-theoretical invariants such as local vertex invariants, e.g. vertex degree v_i (sum of row/column entries in the adjacency matrix) or distance sum s_i (sum of topological distances from a given vertex i to all other vertices). Several frequently used indices (Wiener 1947, Randić 1975, Kier & Hall 1976, 1986, 1999) have been used extensively for QSAR and QSPR studies. I have added a few other TIs, starting with centric indices (Balaban 1979) and following up with the average distance-based connectivity index, known as the Balaban index J (Balaban 1982a, 1983, 2000b, 2002). This molecular invariant for constitutional graphs has a formula which is similar to that for the Randić index, but instead of vertex degrees uses distance sums and takes averages over the number of edges and rings. Interestingly, it was proved that for an infinitely long polyethylene molecule the value of the J index is the number π = 3.14159… (Balaban et al. 1985). Two advantages of basing index J on local vertex invariants derived from the distance matrix instead of the adjacency matrix are the lower degeneracy and the simple way to account for heteroatoms or multiple bonds (Balaban 1986a, Ivanciuc & Balaban 1994, 1998). A spectacular use of TIs that included J and three other TIs, together with other molecular invariants, was published by Lahana and coworkers (Grassy et al. 1998) in the search for immunosuppressive agents: starting from the information about the bioactivity of a few decapeptides in the form of range values for 13 descriptors and varying the nature of 7 amino acids, they reduced the number of starting structures from about 250,000 to 25. Then they performed elaborate calculations reducing further the number of structures to 5, which were prepared and tested. One of these structures had a 100-fold higher immunosuppressive activity than the lead compound.

Other TIs are based on information theory (Bonchev & Trinajstić 1977, Balaban & Balaban 1991). In Trinajstić’s book a chapter is dedicated to TIs (Trinajstić 1992). In collaboration with my Ph. D. student Ioan Motoc and with colleagues Bonchev and Mekenyan from Burgas, Bulgaria, we published an early review on TIs (Balaban et al. 1983). An edited book reviewing all published information on TIs was published in 1999 (Devillers & Balaban 1999) along with two other books on the same topic (Karelson 2000, Todeschini & Consonni 2009). Another edited book contains chapters on molecular descriptors for three-dimensional molecular structures (Balaban 1997). I authored articles on QSAR in encyclopedias upon invitations (Balaban 2000a, 2009b).

9. Collaborations with L.B. Kier, S.C. Basak, D.J. Klein, N.H. March, M. Randić, and I. Gutman

A brief digression is needed here. In 1963 I had been elected as corresponding member of the Romanian Academy, when I was 32 years old. After returning from Vienna in 1970 and resuming my teaching position at the Bucharest Polytechnic University, life in Romania under the communist regime became gradually worse; my sister and my wife’s brother, independently of each other, emigrated illegally and as a consequence my travels abroad were severely curtailed; until the fall of the communist dictatorship in 1989 my wife was never allowed to accompany me abroad. Experimental research in chemistry became almost impossible due to lack of funding and information, so that my publications became mostly theoretical, on graph-theoretical tools for solving problems in chemistry. Through the scientific exchange between the U.S. National Academy of Sciences and the Romanian Academy I was invited to deliver a series of lectures in the USA in 1975. It so happened that when I lectured at Harvard University, Milan Randić was present and decided to center his research on chemical graphs and topological indices, and we started some joint projects. In 1990, shortly after the political change in Romania, I was promoted in the Romanian Academy to the rank of an academician (titular member).

I received in 1991 an invitation from Professor Lemont B. Kier to come to visit him with my wife at the Department of Medicinal Chemistry, School of Pharmacy, Virginia Commonwealth University, in Richmond. This invitation changed my life, and I am deeply grateful to Monty Kier. During three months in the spring of 1991 we worked on QSPR using topological indices and published three joint papers (Balaban et al. 1992a, 1992b, 1992c).

Several book chapters are reviews on topological indices, QSAR, and QSPR (Balaban 2000b, 2002); collaborations with Subhash C. Basak (Natural Resource Research Institute of the University of Minnesota, Duluth) are summarized in another book chapter (Basak et al. 2002).

Before returning from Richmond to Romania, another invitation came to visit the Texas A&M University at Galveston, where I had been invited repeatedly earlier without being allowed to accept previous invitations. Now again this invitation gave another orientation to my future activity because after a few months in Texas I started to teach alternating semesters in Galveston and Bucharest for several years. Then reaching the mandatory retirement age, as is usual in Europe, I took my retirement from the Bucharest Polytechnic and in 2001 I became a tenured professor at the Texas A&M University at Galveston. In 2012 I was awarded the position of Emeritus Professor so as to teach only during the Spring Semesters (the hurricane season coincides with the Fall Semester). In Galveston I performed some experimental investigations in collaboration with Romanian post-doctoral students who accompanied me with their spouses (Drs. Marc Antoniu Ilies and Monica Ilies on pyridinium cationic lipids as gene transfer agents, with the support of Professor William A. Seitz (Ilies et al. 2004, 2006) and also theoretical research (Drs. Ovidiu Ivanciuc and Teodora Ivanciuc (Ivanciuc et al. 2001a, 2001b). For the latter type of research I benefitted from Professor Douglas J. Klein’s vast knowledge in many collaborations from which only a few are mentioned here (Klein & Balaban 2011, Balaban & Klein 2009), namely those that interpreted regularities in properties of folded graphene sheets forming nanotubes, nanocones, or nanotori as being due to congruence or incongruence of Clar sextets. Several collaborations with Klein and Professor Norman H. March involved theoretical interpretations of phase transitions (Balaban et al. 2005b), especially involving ionic liquids (Balaban et al. 2005a, 2007c, 2008a).

Collaborations with my old friend Milan Randić became more frequent and many recent papers have been published concerning partitions of π-electrons in benzenoids (Balaban & Randić 2005, 2008a, 2008b, 2011) or graphical representations of proteins (Randić et al. 2011) and of DNA or RNA (Randić & Balaban 2003, Balaban et al. 2003, Randić et al. 2005). For partitions of π-electrons in heterocyclic compounds (Balaban et al. 2007a, 2008b) or in nonalternant compounds I collaborated with Professor Ivan Gutman (Balaban et al. 2009, Gutman et al. 2009).

10. (3,g)-Cages

One of the most famous graphs is the Petersen graph; it is a non-Hamiltonian cubic graph with 10 vertices, and it is the smallest trivalent graph with girth g = 5 (Holton & Sheehan 1993). Such smallest cubic graphs with given girth (i.e. smallest circuit) are called cages. At the time when I was in Vienna (1967-1970) the cages with girth 4, 5, 6, 7, 8, and 12 were known; all were unique and had 6, 10, 14, 24, 30, and 126 vertices, respectively. There was an obvious gap for the trivalent 9-, 10- and 11-cages. On examining the relationships between these cases I found a regularity and using it together with the conjectured symmetry, I found by trial-and-error the first 10-cage with 70 vertices (Balaban 1972a), which was selected to appear later on the cover of the first edition of a book entitled Pearls in Graph Theory (Hartsfield & Ringel 1990); two other 10-cages were found soon afterwards by other authors (O’Keefe & Wong 1980). Then, based on the observation that one can generate a lower (2k–1)-cage by excising a branched tree from a 2k-cage, I conjectured about the 11-cage with 112 vertices (Balaban 1973), which was obtained by excision of a 14-vertex branched tree from the 12-cage, and it was proved later to be unique, but another conjecture about a graph with girth 9 and 60 vertices was disproved by Biggs who found the first of the 18 possible 9-cages with 58 vertices (Biggs & Hoare 1980). Thus, starting from chemical graphs, I contributed to enriching graph theory with two cubic graphs that are known as the Balaban-10-cage and Balaban-11-cage, respectively. Both these cages have Hamiltonian circuits. The 10-cage (Fig. 9) has three orbits with four 10-circuits (circles), two 10-circuits (squares) and 5 pairs of adjacent vertices (triangles in Fig. 11). My conjectures were proved by long calculations using arrays of parallel computers by Exoo and by Brinkmann and McKay (Exoo & Jajcay 2008, Brinkmann et al. 1995). Nothing is yet proved about trivalent cages with girth g > 12. Just as there are named reactions, there are also named graphs, available from Wolfram (Math World) or Wikipedia, and probably this is the only case when one and the same name appears in both chemical and graph-theoretical repositories.

Figure 11. The Balaban 10-cage

11. Conclusion and outlook

In the preceding section it was mentioned that symmetry considerations directed my search for the 10-cage, taking into account regularities observed among cages with various girths (Balaban 1972a, 1973). Symmetry and its absence (which leads to chirality) pervade art and science and remain as guiding lights for both these human endeavors (Balaban 1986b, 1994a).

In 1993 mathematicians working on graph theory organized a conference in Fairbanks, Alaska with the provocative title Quo Vadis, Graph Theory? inviting also two chemists, Milan Randić and myself. I talked about solved and unsolved problems in chemical graph theory (Balaban 1993b). This reminded me of an earlier contribution to a volume grouping together specialists of various disciplines (social sciences, communication, electrical networks, statistical mechanics, operations research, geography, architecture, linguistics) who were interested in using graph-theoretical tools and methods (Rouvray & Balaban 1979).

In a paper entitled ‘Reflections about mathematical chemistry’ that was published in Foundations of Chemistry (Balaban 2005), I argued that chemical graph theory proves that there exist chemical problems which can be solved without needing the intermediacy of physics, in agreement with ideas on the "emancipation of chemistry" (Thomas 2012). In turn, some of these problems raise questions that may stimulate mathematical research.

References

Avram, M., Nenitzescu, C.D. & Marica, E.: 1957, ‘Untersuchungen in der Cyclobutanreihe. II. Zur Kenntnis des Cyclobutadiens’, Chemische Berichte, 90, 1857-68.

Balaban, A.T.: 1959, ‘An attempt for the systematization of monocyclic aromatic compounds’ Studii si cercetari de chimie, Acad. R. P. Roumania, 7, 257-295 (in Romanian).

Balaban, A.T.: 1966, ‘Chemical graphs. I. Valence isomerism of cyclopolyenes’, Revue Roumaine de Chimie, 11, 1097-1116; Erratum, ibid. 1967, 12, No. 1, 103.

Balaban, A.T.: 1969a, ‘Chemical graphs. VII. Proposed nomenclature of branched cata-condensed benzenoid polycyclic hydrocarbons’, Tetrahedron, 25, 2949-56.

Balaban, A.T.: 1969b, ‘Chemical graphs. Part 50. Symmetry and enumeration of fibonacenes (unbranched catacondensed benzenoids isoarithmic with helicenes and zigzag catafusenes)’, MATCH, Communications in Mathematical and Computational Chemistry, 24, 29-38.

Balaban, A.T.: 1972a, ‘A trivalent graph of girth ten’, Journal of Combinatorial Theory B, 12, 1-5.

Balaban, A.T.: 1972b, ‘Chemical graphs. XIII. Combinatorial patterns’, Revue Roumaine de Mathématiques Pures et Appliquées, 17, 3-16.

Balaban, A.T.: 1973, ‘Trivalent graphs of girth nine and eleven, and relationships among cages’, Revue Roumaine de Mathématiques Pures et Appliquées, 18, 1033-1043.

Balaban, A.T.: 1974, ‘Chemical graphs. XXII. Valence isomers of heteroannulenes or of substituted annulenes. Coisomeric cubic multigraphs’, Revue Roumaine de Chimie, 8, 1323-1342.

Balaban, A.T.: 1976a, ‘Enumeration of catafusenes, diamondoid hydrocarbons and staggered alkane C-rotamers’, MATCH, Communications in Mathematical and Computational Chemistry, 2, 51-61.

Balaban, A.T.: 1976b, ‘Chemical graphs. XXVII. Enumeration and codification of staggered conformations of alkanes’, Revue Roumaine de Chimie, 21, 1049-71.

Balaban, A.T.: 1978, ‘Chemical graphs. XXXII. Constitutional and steric isomers of substituted cycloalkanes’, Croatica Chemica Acta, 51, 35-42.

Balaban, A.T.: 1979, ‘Chemical graphs. XXXIV. Five new topological indices for the branching of tree-like graphs’, Theoretica Chimica Acta, 53, 355-75.

Balaban, A.T.: 1980a, ‘Chemical graphs. XXXVIII. Synthon graphs’, MATCH, Communications in Mathematical and Computational Chemistry, 8, 159-92.

Balaban, A.T.: 1980b, ‘Is aromaticity outmoded?’, Pure and Applied Chemistry, 52, 1409-29.

Balaban, A.T.: 1982a, ‘Highly discriminating distance-based topological index’, Chemical Physics Letters, 80, 399-404.

Balaban, A.T.: 1982b, ‘Challenging problems involving benzenoid polycyclics and related systems’, Pure and Applied Chemistry, 54, 1075-96.

Balaban, A.T.: 1983, ‘Topological indices based on topological distances in molecular graphs’, Pure and Applied Chemistry, 55, 199-206.

Balaban, A.T.: 1986a, ‘Chemical graphs. 48. Topological index J for heteroatom-containing molecules taking into account periodicities of element properties’, MATCH, Communications in Mathematical and Computational Chemistry, 21, 115-22.

Balaban, A.T.: 1986b, ‘Symmetry in chemical structures and reactions’, Computers and Mathematics with Applications, 12B, 999-1020 (reprinted in Symmetry Unifying Human Understanding (I. Hargittai, ed.) Pergamon Press, New York, 1986, pp. 999-1020).

Balaban, A.T.: 1991, ‘Enumeration of isomers’, in: D. Bonchev & D.H. Rouvray (eds.), Chemical Graph Theory. Introduction and Fundamentals, New York: Abacus Press, Gordon and Breach, pp. 177-234.

Balaban, A.T.: 1993a, ‘Confessions and reflections of a graph-theoretical chemist’, MATCH, Communications in Mathematical and Computational Chemistry, 29, 3-17.

Balaban, A.T.: 1993b, ‘Solved and unsolved problems in chemical graph theory’, Annals of Discrete Mathematics, 55, 109-126 (reprinted in: J. Gimbel, J.W. Kennedy & L.V. Quintas (eds.), Quo Vadis, Graph Theory? A Source Book for Challenges and Directions, North Holland, Amsterdam).

Balaban, A.T.: 1994a, ‘Symmetry of graphs’, in: D. Bonchev & D.H. Rouvray (eds.), Chemical Group Theory. Introduction and Fundamentals, New York: Abacus Press, Gordon and Breach, pp. 155-208.

Balaban, A.T.: 1994b, ‘Reaction graphs’, in: D. Bonchev & O. Mekenyan (eds.), Graph Theoretical Approaches to Chemical Reactivity, Kluwer, Dordrecht, 1994, pp. 137-180.

Balaban, A.T.: 1995, ‘Chemical graphs: looking back and a glimpse ahead’, Journal of Chemical Information and Computer Science, 35, 339-350.

Balaban, A.T. (ed.): 1997, From Chemical Topology to Three-Dimensional Geometry, New York: Plenum.

Balaban, A.T.: 2000a, ‘QSAR and computational methods in drug discovery’, in: R.A. Meyers (ed.), Encyclopedia of Analytical Chemistry", Chichester: Wiley, vol. 8, pp. 7288-311.

Balaban, A.T. 2000b, ‘A personal view about topological indices for QSAR/QSPR’, in: M. Diudea (ed.), QSAR/QSPR Studies by Molecular Descriptors, New York: Huntington, pp. 1-25.

Balaban, A.T.: 2002, ‘A comparison between various topological indices, particularly index J and Wiener’s index W’, in: D.H. Rouvray & R.B. King (eds.), Topology in Chemistry: Discrete Mathematics of Molecules, Chichester: Horwood, pp. 89-112.

Balaban, A.T.: 2005, ‘Reflections about mathematical chemistry’, Foundations of Chemistry, 7, 289-306.

Balaban, A.T.: 2009a, ‘Aromaticity of six-membered rings with one heteroatom’, in: T.M. Krygowski & M.K. Cyranski (eds.), Topics in Heterocyclic Chemistry, vol. 19, Aromaticity in Heterocyclic Compounds, New York: Springer, pp. 203-46.

Balaban, A.T.: 2009b, ‘Molecular descriptors in drug design’, in: R.A. Meyers (ed.), Encyclopedia of Complexity and Systems Science, New York: Springer, Part 4, pp. 2196-215.

Balaban, A.T.: 2010, ‘Monocyclic hetarenes with π-electron aromatic sextet’, in: A.R. Katritzky (ed.), Advances in Heterocyclic Chemistry, Vol. 99, Amsterdam: Elsevier, pp. 61-105.

Balaban, A.T.: 2011a, ‘Autobiographical notes: 80 years of age, 68 years of chemistry’, MATCH, Communications in Mathematical and Computational Chemistry, 66, 7-32.

Balaban, A.T.: 2011b, ‘Balaban–Nenitzescu–Praill Reaction’, in: J.J. Li (ed.), Name Reactions in Heterocyclic Chemistry II, Hoboken, NJ: Wiley, pp. 402-19.

Balaban, A.T.: 2012a, ‘A personal view of chemistry (with emphasis to mathematical chemistry) as science and art’, Internet Electronic Journal of Molecular Design, 11, 1-22.

Balaban, A.T.: 2012b, ‘Brief review of contributions to organic chemistry’, Revue Roumaine de Chimie, 57, 535-57.

Balaban, A.T.: 2012c, ‘Partitioned-formula tables for diamond hydrocarbons (diamondoids)’, Journal of Chemical Information and Modeling, 52, 2856-69.

Balaban, A.T.: 2013a, ‘Diamond hydrocarbons revisited. Partitioned formula tables of diamondoids’, Journal of Mathematical Chemistry, 51, 1043-55.

Balaban, A.T.: 2013b, ‘Diamond hydrocarbons and related structures,’ in: M.V. Diudea & C.L. Nagy (eds.), Diamond and Related Nanostructures, Berlin: Springer, pp. 1-27.

Balaban, A.T. & Balaban, T.S.: 1991, ‘New vertex invariants and topological indices of chemical graphs based on information on distances’, Journal of Mathematical Chemistry, 8, 383-397.

Balaban, A.T. & Bonchev, D.: 2005, ‘Complexity, sphericity, and ordering of regular and semiregular polyhedra’, MATCH, Communications in Mathematical and Computational Chemistry, 54, 137-152.

Balaban, A.T. & Harary, F.: 1967, ‘Chemical graphs. IV. Dihedral groups and monocyclic aromatic compounds’, Revue Roumaine de Chimie, 12, 1511-15.

Balaban, A.T. & Harary, F.: 1968, ‘Chemical graphs. V. Enumeration and proposed nomenclature of benzenoid cata-condensed polycyclic aromatic hydrocarbons’, Tetrahedron, 24, 2505-16.

Balaban, A.T. & Harary, F.: 1971, ‘The characteristic polynomial does not uniquely determine the topology of a molecule’, Journal of Chemical Documentation, 11, 258-259.

Balaban, A.T. & Harary, F.: 1976, ‘Early history of the interplay between graph theory and chemistry’, in: A.T. Balaban (ed.), Chemical Applications of Graph Theory, London: Academic Press, pp. 1-4.

Balaban, A.T. & Kerek, F.: 1974, ‘Chemical graphs. XX. Graphs of parallel and/or subsequent substitution reactions’, Revue Roumaine de Chimie, 19, 631-647.

Balaban, A.T. & Klein, D.J.: 2009, ‘Claromatic carbon nano-structures’, Journal of Physical Chemistry C, 113, 19123-33.

Balaban, A.T. & Nenitzescu, C.D.: 1964, ‘Dehydrogenating Condensations of Aromatics (Scholl and Related Reactions)’, in: G.A. Olah (ed.), Friedel-Crafts and Related Reactions, New York: Wiley, vol. 2, pp. 979-1047.

Balaban, A.T. & Randić, M.: 2005, ‘Partitioning of π-electrons in rings of polycyclic conjugated hydrocarbons. Part 6. Comparison with other methods for estimating the local aromaticity of rings in polycyclic benzenoids’, Journal of Mathematical Chemistry, 37, 443-453.

Balaban, A.T. & Randić, M.: 2008a, ‘Ring signatures for benzenoids with up to seven rings. Part 1. Catacondensed systems’, International Journal of Quantum Chemistry, 108, 865-97.

Balaban, A.T. & Randić, M.: 2008b, ‘Ring signatures for benzenoids with up to seven rings. Part 2. Pericondensed systems’, International Journal of Quantum Chemistry, 108, 898-926.

Balaban, A.T. & Randić, M.: 2011a, ‘Structural approach to aromaticity and local aromaticity in conjugated polycyclic systems’, in: M.V. Putz (ed.), Carbon Bonding and Structures. Advances in Physics and Chemistry, Dordrecht: Springer, pp. 159-204.

Balaban A.T. & Randić, M.: 2011b, ‘Structural Approach to Aromaticity and Local Aromaticity in Conjugated Polycyclic Systems’, in: M.V. Putz (ed.), Carbon Bonding and Structures: Advances in Physics and Chemistry, Dordrecht et al.: Springer, pp. 159-204.

Balaban, A.T. & Schleyer, P.v.R.: 1978, ‘Systematic classification and nomenclature of diamond hydrocarbons. 1. Graph-theoretical enumeration of polymantanes’, Tetrahedron, 34, 3599-609.

Balaban, A.T. & Simon, Z.: 1962, ‘Aromaticity constants’, Tetrahedron, 18, 315-21.

Balaban, A.T. & Tomescu, I.: 1983, ‘Algebraic expressions for the number of Kekulé structures of isoarithmic cata-condensed polycyclic hydrocarbons’, MATCH, Communications in Mathematical and Computational Chemistry, 14, 155-82.

Balaban, A.T. & Tomescu, I.: 1984, ‘Chemical graphs. XL. Three relations between the Fibonacci sequence and the numbers of Kekulé structures for non-branched cata-condensed polycyclic aromatic hydrocarbons’, Croatica Chemica Acta, 57, 391-404.

Balaban, A.T. & Tomescu, I.: 1985, ‘Chemical graphs. XLI. Numbers of conjugated circuits and Kekulé structures for zigzag catafusenes and (j,k)-hexes: generalized Fibonacci numbers’, MATCH, Communications in Mathematical and Computational Chemistry, 17, 91-120.

Balaban, A.T. & Tomescu, I.: 1988, ‘Alternating 6-cycles in perfect matchings of graphs representing condensed benzenoid hydrocarbons’, Discrete Appl. Math., 19, 5-16 (reprinted in: J.W. Kennedy & L.W. Quintas (eds.), Applications of Graphs in Chemistry and Physics, Amsterdam: North-Holland, pp. 5-16).

Balaban, A.T.; Barabas, A. & Arsene, A.: 1964a, ‘1,3,2-Dioxaborinium and 4,5-benzo-1,3,2-dioxaborinium cations, novel aromatic systems’, Tetrahedron Letters, 5, 2721-4.

Balaban, A.T.; Arsene, A.; Bally, I.; Barabas, A.; Paraschiv, M. & Romas, E.: 1964b, ‘1,3,2-Dioxaborinium (boroxaropyrylium) salts and their decomposition to bis-1,3-diketonatoboronium salts’, Tetrahedron Letters, 5, 3917-23.

Balaban, A.T.; Farcasiu, D. & Banica, R.: 1966, ‘Chemical graphs. II. Graphs of multiple 1,2-shifts in carbonium ions and related systems’, Revue Roumaine de Chimie, 11, 1205-27.

Balaban, A.T.; Arsene, A.; Bally, I.; Barabas, A.; Paraschiv, M.; Roman, M. & Romas, E.: 1970a, ‘ Heterocyclic organoboron compounds. XII. 2,4,6-Trisubstituted-1,3,2-dioxaborinium salts’, Revue Roumaine de Chimie, 15, 635-53.

Balaban, A.T.; Davies, R.O.; Harary, F.; Hill, A. & Westwick, R.: 1970b, ‘Cubic identity graphs and planar graphs derived from trees’, Australian Journal of Mathematics, 11, 207-15.

Balaban, A.T.; Dinculescu, A.; Dorofeenko, G.N.; Fischer, G.W.; Koblik, A.V.; Mezheritskii, V.V. & Schroth, W.: 1982, Pyrylium Salts. Syntheses, Reactions and Physical Properties (Advances in Heterocyclic Chemistry, Suppl. Vol. 2), New York: Academic Press.

Balaban, A.T.; Motoc, I.; Bonchev, D.; & Mekenyan, O.: 1983, ‘Topological indices for structure-activity correlations’, Steric Effects in Drug Design (Topics in Current Chemistry), 114, 21-55.

Balaban, A.T.; Ionescu-Pallas, N. & Balaban, T.S.: 1985, ‘Asymptotic values of topological indices J and J’ (average distance sum connectivities) for infinite acyclic and cyclic graphs’, MATCH, Communications in Mathematical and Computational Chemistry, 17, 121-46.

Balaban, A.T.; Banciu, M. & Ciorba, V.: 1986, Annulenes, Benzo-, Hetero-, Homo-Derivatives and Their Valence Isomers, Boca Raton, FL: CRC Press, 3 volumes.

Balaban, A.T.; Brunvoll, J.; Cioslowski, J.; Cyvin, B.N.; Cyvin, S.J.; Gutman, I.; Wenchen, H; Wenjie, H; Knop, J.V.; Kovacevic, M.; Müller, W.R.; Szymanski, K.; Tosic, R.; & Trinajstić, N.: 1987, ‘Enumeration of benzenoid and coronoid hydrocarbons’, Zeitschrift für Naturforschung, 42c, 863-70.

Balaban, A.T.; Joshi, N.; Kier, L.B. & Hall, L.H.: 1992a, ‘Correlations between chemical structure and normal boiling points of halogenated alkanes C₁-C₄’, Journal of Chemical Information and Computer Science, 32, 233-7.

Balaban, A.T.; Kier, L.B. & Joshi, N.: 1992b, ‘Correlation between chemical structure and normal boiling points of acyclic ethers, peroxides, acetals,and their sulfur analogues’, Journal of Chemical Information and Computer Science, 32, 237-44.

Balaban, A.T.; Kier, L.B. & Joshi, N.: 1992c, ‘Structure-property analysis of octane numbers for hydrocarbons (alkanes, cycloalkanes, alkenes)’, MATCH, Communications in Mathematical and Computational Chemistry, 28, 13-27.

Balaban, A.T.; Plavsić, D. & Randić, M.: 2003, ‘DNA invariants based on nonoverlapping triplets of nucleotide bases’, Chemical Physics Letters, 379, 147-54.

Balaban, A.T.; Oniciu, D.; & Katritzky, A.R.: 2004, ‘Aromaticity as a cornerstone in heterocyclic chemistry’, Chemical Reviews, 104, 2777-812.

Balaban, A.T.; Klein, D.J.; March, N.H. & Matthai, C.C.: 2005a, ‘Transport and thermodynamic properties in low melting point ionic liquids related to n-alkyl chain length’, Physics and Chemistry of Liquids, 43, 403-7.

Balaban, A.T.; Klein, D.J.; March, N.H.; Tosi, M.P. & Ausloos, M.: 2005b, ‘Phase transition regularities in critical constants, fusion temperatures and enthalpies of some chemically similar chainlike structures’, ChemPhysChem, 6, 1741-5.

Balaban, A.T.; Gutman, I. & Stanković, S.: 2007a, ‘Partitioning of π-electrons in rings of aza-derivatives of polycyclic benzenoid hydrocarbons’, Polycyclic Aromatic Compounds, 27, 51-6.

Balaban, A.T.; Klein, D.J.; Dahl, J.E. & Carlson, R.M.K.: 2007b, ‘Molecular descriptors for natural diamondoid hydrocarbons and quantitative structure-property relationships for their chromatographic data’, The Open Organic Chemistry Journal, 1, 13-31.

Balaban, A.T.; Klein, D.J.; & March, N.H.: 2007c, ‘Aqueous solutions of a "green" ionic liquid and of lithium chloride compared and contrasted’, Physics and Chemistry of Liquids, 45, 597-600.

Balaban, A.T., March, N.H. & Klein, D.J.: 2008a, ‘Melting points and other properties of ionic liquids, with emphsis on the pressure dependence’, Physics and Chemistry of Liquids, 46, 682-6.

Balaban, A.T., Gutman, I. & Stanković, S.: 2008b, ‘Effect of heteroatoms on partitioning of π-electrons in rings of catafusenes’, Polycyclic Aromatic Compounds, 28, 85-97.

Balaban, A.T.; Durdević, J. & Gutman, I.: 2009, ‘Comments on π-electron conjugation in the five-membered ring of benzo-derivatives of corannulene’, Polycyclic Aromatic Compounds, 29, 185-208.

Balaban, T.S . & Balaban, A.T.: 2003, ‘Pyrylium Salts’, in: Science of Synthesis; Houben-Weyl Methods of Molecular Transformations, Stuttgart: Thieme, vol. 14, pp. 11-200.

Basak, S.C.; Mills, D.; Gute, B.D.; Grunwald, G.D. & Balaban, A.T.: 2002, ‘Applications of topological indices in predicting property/bioactivity/toxicity of chemicals’, in: D.H. Rouvray & R.B. King (eds.), Topology in Chemistry: Discrete Mathematics of Molecules, Chichester: Horwood, pp. 113-84.

Biggs, N.L. & Hoare, M.J.: 1980, ‘A trivalent graph with 58 vertices and girth 9’, Discrete Mathematics, 30, 299-301.

Bonchev, D. & Trinajstić, N.: 1977, ‘Information theory, distance matrix, and molecular branching’, Journal of Chemical Physics, 67, 4517-33.

Brinkmann, G.; McKay, B. & Saager, K.: 1995, ‘The smallest cubic graphs with girth nine’, Combinatorics, Probability, and Computing, 4, 317-9.

Brinkmann, G; Caporossi, G. & Hansen, P.: 2003, ‘A survey and new results on computer enumeration of polyhex and fusene hydrocarbons’, Journal of Chemical Information and Computer Science, 43, 842-51.

Corey, E.J.: 1990, ‘The logic of chemical synthesis: multistep synthesis of complex carbogenic molecules (Nobel Lecture)’, Angewandte Chemie, International Edition, 30, 455-65.

Corey, E.J. & Cheng, X.M.: 1989, The Logic of Chemical Synthesis, New York: Wiley.

Corey, E.J. & Wipke, W.T.: 1969, ‘Computer-assisted design of complex organic syntheses’, Science, 166, 178-92.

Dahl, J.E.; Liu, S.G. & Carlson, R.M.K.: 2003, ‘Isolation and structure of higher diamondoids, nanometer-sized diamond molecules’, Science, 299, 96-9.

De Bruin, K.E.; Naumann, K.; Zon, G. & Mislow, K.: (1969), ‘Topological representations of the stereochemistry of displacement reactions of phosphorus in phosphonium salts and cognate systems’, Journal of the American Chemical Society, 91, 7031-40.

Devillers, J. & Balaban, A.T. (eds.): 1999, Topological Indices and Related Descriptors in QSAR and QSPR, Amsterdam: Gordon and Breach.

Doering, W.v.E. & Rosenthal, J.W.: 1966, ‘9,10-Dihydronaphthalene. Formation from bullvalene and Nenitzescu’s hydrocarbon, thermal reorganization, and photorearrangement to bullvalene’, Journal of the American Chemical Society, 88, 2078-9.

Dunitz, J.D. & Prelog, V.: 1968, ‘Ligand reorganisation in trigonal-bipyramids’, Angewandte Chemie, International Edition in English, 7, 725-6.

Engler, E.M.; Farcasiu, M.; Sevin, A.; Cense, J.M.;& Schleyer, P.V.R.: 1973, ‘Mechanism of adamantane rearrangements’, Journal of the American Chemical Society, 95, 5769-71.

Exoo, G. & Jajcay, R.: 2008, ‘Dynamic cage survey’, Electronic Journal of Combinatorics, September, 15-16.

Grassy, G.; Calas, B.; Yasri, A.; Lahana, R.; Woo, J.; Iyer, S.; Kaczorek, M; Floc'h, R. & Buelow, R.: 1998, ‘Computer-assisted rational design of immunosuppressive compounds’, Nature Biotechnology, 16, 748-52.

Gutman, I. & Klavžar, S.: 2006, ‘Chemical graph theory of fibonacenes’, MATCH, Communications in Mathematical and Computational Chemistry, 55, 39-54.

Gutman, I.; Durdević, J. & Balaban, A.T.: 2009, ‘A regularity for cyclic conjugation in acenaphthylene, fluoranthene and their congeners’, Polycyclic Aromatic Compounds, 29, 3-11.

Harary, F.: 1969, Graph Theory, Reading, MA: Addison-Wesley.

Hartsfield, N. & Ringel, G.: 1990, Pearls in Graph Theory. A Comprehensive Introduction, San Diego: Academic Press.

Hassner, A. & Stumer, C.: 2002, Organic Syntheses Based on Name Reactions, 2^nd ed., Amsterdam: Pergamon-Elsevier, p. 17.

Heller, J.: ‘Höhere Koordinationen von Hauptgruppenelementen’, Chimia (Aarau), 23, 351-362.

Hendrickson, J.B.: 1977, ‘Systematic synthesis design. 6. Yield analysis and convergency’, Journal of the American Chemical Society, 99, 5439-50.

Herndon, W.C.: 1974, Thermochemical parameters for benzenoid hydrocarbons’, Thermochimica Acta, 8, 225-37.

Holton, D.A. & Sheehan, J.: 1993, The Petersen Graph (Australian Mathematical Society Lecture Series 7), Cambridge: Cambridge Univ. Press.

Hosoya, H.: 1971, ‘Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons’, Bulletin of the Chemical Society of Japan, 44, 2332-9.

Ilies, M.A.; Seitz, W.A.; Ghiviriga, I.; Johnson, B.H.; Miller, A.L.; Thompson, E.B. & Balaban, A.T.: 2004, ‘Pyridinium cationic lipids in gene delivery: a structure-activity correlation study’, Journal of Medicinal Chemistry, 47, 3744-54.

Ilies, M.A; Seitz, W.A.; Johnson, B.H.; Ezell, E.L.; Miller, A.L.; Thompson E.B. & Balaban, A.T.: 2006, ‘Lipophilic pyrylium salts in the synthesis of efficient pyridinium-based cationic lipids, gemini surfactants, and lipophilic oligomers for gene delivery’, Journal of Medicinal Chemistry, 49, 3872-87.

Imrich, W. & Klavžar, S.: 2000, Product Graphs. Structure and Recognition, New York: Wiley, 2000.

Imrich, W.; Klavžar, S. & Rall, D.F.: 2008, Graphs and Their Cartesian Product, Topics in Graph Theory, Berlin: Springer.

Ivanciuc, O. & Balaban, A.T.: 1994, ‘ Design of topological indices. Part 5. Precision and error in computing graph theoretic invariants for molecules containing heteroatoms and multiple bonds’, MATCH, Communications in Mathematical and Computational Chemistry, 30, 117-39.

Ivanciuc, O.; Ivanciuc, T. & Balaban, A.T.: 1998, ‘Design of topological indices. Part 10. Parameters based on electronegativity and covalent radius for the computation of molecular graph descriptors for heteroatom-containing molecules’, Journal of Chemical Information and Computer Science, 38, 395-401.

Ivanciuc, O.; Ivanciuc, T.; Klein, D.J.; Seitz, W.A. & Balaban, A.T.: 2001a, ‘Quantitative structure-retention relationships for gas chromatographic retention indices of alkylbenzenes with molecular graph descriptors. SAR and QSAR in Environmental Research, 11, 419-52.

Ivanciuc, O.; Ivanciuc, T.; Klein, D.J.; Seitz, W. . & Balaban, A.T.: 2001b, ‘Wiener index extension by counting even/odd graph distances’, Journal of Chemical Information and Computer Science, 41, 536-549.

Karelson, M.: 2000, Molecular Descriptors in QSAR/QSPR, New York: Wiley.

Kier, L.B. & Hall, L.H.: 1976, Molecular Connectivity in Chemistry and Drug Research, New York: Academic Press.

Kier, L.B. & Hall, L.H.: 1986, Molecular Connectivity in Structure-Activity Analysis, Letchworth: Research Studies Press.

Kier, L.B. & Hall, L.H.: 1999, Molecular Structure Description: The Electrotopological State, New York: Academic Press.

Klavžar, S. & Petra, Ž.: 2005, ‘Fibonacci cubes are the resonance graphs of fibonacenes’, Fibonacci Quarerly, 43, 269-76.

Klein, D.J. & Bytautas, L.: 2000, ‘Directed reaction graphs as posets’, MATCH, Communications in Mathematical and Computational Chemistry, 42, 261-90.

Klein, D.J. & Balaban, A.T.: 2011, ‘Clarology for conjugated carbon nanostructures: molecules, polymers, graphene, defected graphene, fractal benzenoids, fullerenes, nanotubes, nanocones, nanotori, etc.’, The Open Organic Chemistry Journal, 5 (Suppl. 1-M1), 27-61.

Lauterbur, P.C. & Ramirez, F.: 1966, ‘Pseudorotation in trigonal-bipyramidal molecules’, Journal of the American Chemical Society, 90, 6722-6.

Mislow, K.: 1970, ‘Role of pseudorotation in the stereochemistry of nucleophilic displacement reactions’, Accounts of Chemical Research, 3, 321-31.

Mislow, K. & Zon, G.: 1971, ‘Phosphorus stereochemistry’, Topics in Current Chemistry, 19, 61-94.

Nenitzescu, C.D. & Balaban, A.T.: 1964, ‘Aliphatic Acylation’, in: G.A. Olah (ed.), Friedel-Crafts and Related Reactions, New York: Wiley, vol. 3, pp. 1033-152.

O’Keefe, M. & Wong, P.K.: 1980, ‘A smallest graph of girth 10 and valency 3’, Journal of Combinatorial Theory, Series B, 12, 1-5.

Randić, M.: 1975, ‘On characterization of molecular branching’, Journal of the American Chemical Society, 97, 6609-75.

Randić, M. & Balaban, A.T.: 2003, ‘On a four-dimensional representation of DNA primary sequences’, Journal of Chemical Information and Computer Science, 43, 532-9.

Randić, M.; Klein, D.J.; El-Basil, S. & Calkins, P., 1996: ‘Resonance in Large Benzenoid Hydrocarbons’, Croatica Chemica Acta, 69, 1639-60.

Randić, M.; Lers, N.; Plavsić, D.; Basak, S.C. & Balaban, A.T.: 2005, ‘Four-color map representation of DNA or RNA sequences and their numerical characterization’, Chemical Physics Letters, 407, 205-8.

Randić, M.; Zupan, J.; Balaban, A.T.; Vikić-Topić, D. & Plavsić, D.: 2011, ‘On graphical representation of proteins’, Chemical Reviews, 111, 790-862.

Rouvray, D.H.: 1971, ‘Graph theory in chemistry’, Royal Institute of Chemistry Reviews, 4, 173-95.

Rouvray, D.H.: 1974, ‘Isomer enumeration methods’, Chemical Society Reviews, 3, 355-72.

Rouvray, D.H. & Balaban, A.T.: 1979, ‘Chemical Applications of Graph Theory’, in: R.J. Wilson & L.W. Beineke (eds.), Applications of Graph Theory, London: Acadmic Press, pp. 177-221.

Thomas, G.F.: 2012, ‘The emancipation of chemistry’, Foundations of Chemistry, 14, 109-55.

Todeschini, R. & Consonni, V.: 2009, Molecular Descriptors for Chemoinformatics, New York: Wiley-VCH.

Trinajstić, N.: 1992, Chemical Graph Theory, 2^nd edn., Boca Raton, FL: CRC Press.

Vukičević, D. & Balaban, A.T.: 2008, ‘Note on ordering and complexity of Platonic and Archimedean polyhedra based on solid angles’, Journal of Mathematical Chemistry, 44, 725-30.

Whitlock Jr., H.W. & Siefken, M.W.: 1969, ‘The tricyclo[4.4.0.0^3,8]decane to adamantane rearrangement’, Journal of the American Chemical Society, 90, 4929-39.

Wiener, H.: 1947, ‘Structural determination of paraffin boiling points’, Journal of the American Chemical Society, 69, 17-20.

Živković, T. P.; Klein, D.J. & Schmalz, T.G.: 2000, ‘Covalent isoresonance’, Polycyclic Aromatic Compounds, 13, 457-71.

Alexandru T. Balaban:
Texas A&M University at Galveston, Dept. Marine Sciences, Galveston TX 77553-1675, USA; balabana@tamug.edu