Gender in the Substance of Chemistry, Part 1:
The Ideal Gas
Ágnes Kovács*
Abstract: This two-part paper is about the possibility of analyzing the content of chemistry from a gender perspective. The first part provides an example of what such an analysis would look like. The second part is an outline of the theoretical perspective that makes the analysis possible. The example is the model of the ideal gas, the cornerstone of the theory of matter in chemical thermodynamics. I argue that this model is built on fundamental philosophical assumptions (Platonic idealism, hierarchy among states of matter, atomism/individualism, and the negligence of interrelationships among parts and of their embodiment) that have been problematized by feminist scholarship. The same patterns are evident in the treatment of ideal and real solutions in chemical thermodynamics. I argue that it is possible to imagine a theory that utilizes different philosophical ideas and which therefore would be more compatible with feminist values.
Keywords: chemical thermodynamics, models, idealization, gender, values in science.
1. Introduction
If one starts to think about the possible ways in which gender can be brought in relation to chemistry, or indeed to science in general, it is useful to distinguish three approaches. First, we can do research on women in science; second, we can criticize scientific constructions of women, and third, we can investigate if gender ideology is mediated by scientific theories in a more indirect sense (Keller 1992, p. 7, n5).
Obviously, the ‘women in science’ topic is about the process of doing science, while the second and the third topics concern scientific theories, the intellectual product of this process. There is a certain asymmetry between the feminist critique of the life sciences and that of the physical sciences in this respect. Feminist perspectives on evolutionary biology, animal behavior studies, behavioral neuroendocrinology, and human origins have convincingly demonstrated how gender bias on the researchers’ part shapes not only the process but also the outcome of research in these fields (Longino & Doell 1983, Bleier 1984, Haraway 1989, Hubbard 1990, Martin 1991, Fausto-Sterling 1992, Spanier 1995, Gowaty 2003). The feminist critique of the physical sciences, however, has largely remained focussed on scientific knowledge production, leaving issues of content unaddressed.
I believe the reason for this asymmetry is that there is a conceptual and methodological breach between the life sciences and the physical sciences. The life sciences study organisms which do have sex and gender, or at least can be seen as having one. However, since the objects of research in the physical sciences are neither overtly nor projectively gendered, it is not obvious where to start if one wants to discover gender-related values in their theories. How is gender ideology expressed in the content of these fields?
In this two-part paper, I attempt to develop a methodological and epistemological framework which makes it possible to perform a philosophical analysis of the content of the physical sciences from a gender perspective (Part 2). I illustrate the usefulness of this framework by an analysis of the model of the ideal gas in chemical thermodynamics, a branch of physical chemistry (Part 1).[1]
My central thesis is that in the theories of the physical sciences, cultural values (and gender-related ones, among these) are to be found in the principles of natural philosophy utilized by the theory. When looking for gender ideology in the substance of chemistry (in chemical theory, that is), I am looking for general metaphysical principles which serve as the conceptual foundation for the scientific theory in question, and which, in other contexts, constitute the philosophical foundations of a worldview that legitimates gender inequality.
My source for chemical thermodynamics is Atkins’ Physical Chemistry (Atkins & de Paula 2006), a standard text in tertiary chemistry education, currently in its 9th edition.[2] I take the textbook to be the synthesis of a discipline; my focus is not on the idiosyncrasies of Peter Atkins as an author, but rather, on features that would characterize any and every presentation of the same theory. I perform the analysis of chemical thermodynamics in a fashion that is commonly used in the philosophy of chemistry, i.e., identifying the conceptual structure of the theory (Sections 2 and 3) and analyzing the concepts for the philosophical ideas they contain (Section 4). I then link the philosophical ideas to cultural value systems (Section 5). Finally, I sketch an alternative model which is the obverse of the current one in all the aspects that I claim to be problematic from a feminist point of view (Section 6).
2. The properties of gases
The first chapter of Atkins’ Physical Chemistry is titled "The properties of gases" (Atkins & de Paula 2006, pp. 3-14).[3] The ideal or perfect gas[4] is a theoretical construct which is used to explain the properties of more complex systems, such as real gases, and in later chapters, solutions. In accordance with the idea of proceeding from simple systems to more complicated ones, the chapter is divided into two parts: ‘The perfect gas’, and ‘Real gases’, respectively.
Thermodynamics is conducted under a system-centered view of the universe; the unit of analysis is the thermodynamic system. The physical state of a system is defined by its physical properties, such as volume (V), pressure (p), amount of substance (n), and temperature (T). The physical properties are not independent quantities; they are connected by a mathematical relationship called the equation of state, which, in principle, must be determined empirically for each thermodynamic system. Through the synthesis of a wide range of experimental data, thermodynamic theory aims to arrive at an equation of state that describes as many thermodynamic systems as possible – all gases, for example. This is precisely the goal of the textbook chapter under consideration.[5]
The equation of state for a perfect gas is the perfect gas equation (p. 8, equation 1.8):
pV = nRT
Alternatively (p. 19, Table 1.7):
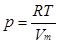
where R (the gas constant) is a constant of nature that has the same value for all gases. Vm is the molar volume of the gas and it equals to V/n. A perfect or ideal gas is a gas that obeys the perfect gas equation under all conditions.
The molecular interpretation of the ideal gas law is the kinetic theory of gases (pp. 748-60), which rests on three fundamental assumptions. First, the gas consists of molecules in ceaseless random motion. Second, the molecules interact only through brief, infrequent and elastic collisions.[6] Third, their size is negligible, in the sense that their diameters are much smaller than the average distance travelled between collisions. The molecules are constantly bumping into the walls of the container, and the pressure comes from the kinetic energy transmitted to the wall in this way. In the kinetic theory of gases, all physical properties of the gas (in particular, pressure and temperature) are traced back to the mechanical behavior of individual molecules.
Real gases do not always obey the perfect gas equation because their molecules interact with one another and have a certain extension in space. Therefore, the perfect gas equation needs to be modified so as to incorporate the effects of repulsive and attractive forces between the molecules and the non-zero volume taken up by them. Atkins describes the effect of the intermolecular forces as follows:
Real gases show deviations from the perfect gas law because molecules interact with one another. Repulsive forces between molecules assist expansion and attractive forces assist compression [p. 14].
The repulsive and attractive forces are assessed for their effect on compressibility, that is, the change of volume with pressure:
At low pressures, when the sample occupies a large volume, the molecules are so far apart for most of the time that the intermolecular forces play no significant role, and the gas behaves virtually perfectly. At moderate pressures, when the average separation of the molecules is only a few molecular diameters, the attractive forces dominate the repulsive forces. In this case, the gas can be expected to be more compressible than a perfect gas because the forces help to draw the molecules together. At high pressures, when the average separation of the molecules is small, the repulsive forces dominate and the gas can be expected to be less compressible because now the forces help to drive the molecules apart [ibid., emphasis mine].
To treat non-ideal behavior quantitatively, a compression factor (Z) is defined. Z is the ratio of the molar volume of a real gas to the molar volume of a perfect gas at the same temperature and pressure. In this way, all non-ideal behavior is condensed into Z: "Because for a perfect gas Z = 1 under all conditions, deviation of Z from 1 is a measure of departure from perfect behaviour" (p. 15).
For real gases, Z can be determined experimentally, and its value varies with pressure as well as with temperature. Indeed, Atkins contains a figure which plots Z as a function of pressure, for several gases, at 0 oC (Figure 1).
Using Z to take account of non-ideal behavior, the gas equation for real gases becomes:
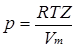
Apart from this adjustment of the perfect gas equation to fit real gases, Atkins relates four more equations of state that take account of intermolecular forces and/or molecular volume and are thus better suited to describe the properties of real gases (p. 19, Table 1.7). The first is the virial equation of state:
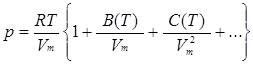
where B is the second virial coefficient, C is the third, etc. and all vary with the temperature. The coefficients are substance-specific constants to be determined empirically for each substance and each temperature. In fact, the term in the parentheses {} can be identified with the compression factor Z, which itself is temperature-dependent.
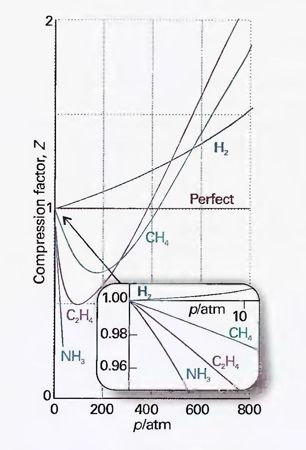
Figure 1: "The variation of the compression factor, Z, with pressure for several gases at 0 oC. A perfect gas has Z = 1 at all pressures". Source: Atkins & de Paula 2006, p. 15, Fig. 1.14, by permission of Oxford University Press
The second equation of state for real gases is the van der Waals equation:
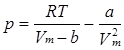
Constants a and b are called the van der Waals coefficients. They are characteristic of each gas but independent of the temperature. In contrast to the virial equation, here a physical meaning is attributed to the constants: a stands for attractive and repulsive forces, and b is the volume taken up by the molecules.
The third and fourth equations of state are the Berthelot equation of state:

and the Dieterici equation of state:

Both describe the pressure of the gas in terms of V, R, T, Vm and constants a and b, respectively, in a more complicated fashion than the van der Waals equation does.
The perfect gas equation and the four equations of state for real gases are all attempts to find a mathematical formula that accounts for as many experimental data (measurements of physical properties of particular substances under various physical conditions) as possible. Each equation complies with some, but none accounts for all. Thus the ideal gas law is roughly accurate for weakly polar gases at low pressures and moderate temperatures, but it becomes increasingly inaccurate for higher pressures and lower temperatures, circumstances which bring about the condensation of a gas to liquid. The van der Waals equation, which is widely used in chemistry education for historical and didactic reasons, is an improvement over the ideal gas law, as it conceives of molecules as particles with volume, not material points, and it also takes intermole cular forces into account. Due to these modifications, it is true for a wider range of substances and physical conditions, but it is not universally valid. At present, there is no equation of state that would accurately predict the properties of all substances under all conditions.
3. The thermodynamics of solutions
In Atkins’ textbook, the thermodynamic description of gases serves as a model for the description of solutions (pp. 148-66). A solution is either (1) a mixture of liquids where the amount of one considerably outweighs the other, or (2) a solid substance (the solute) dissolved in a liquid (the solvent). Solutions are thus mixtures, and so their thermodynamic properties are described in Chapter 5 ("Simple mixtures", pp. 136-73). This chapter starts with discussing the mixing of ideal gases, goes on to mix real gases, and then turns to solutions. The mixing of gases is presented first because the equations obtained here are used in the description of solutions later. Liquids are modeled on the gas state, and the gas state is modeled on the ideal gas.
Mixing is a spontaneous change of composition. According to thermodynamic theory, spontaneous changes in nature are accompanied, and indeed driven, by an increase in entropy (S). Under constant pressure and temperature, which is often the case for chemical systems, this is equivalent to a decrease in the Gibbs free energy (G). S and G are functions of the physical properties (p, T, V, and n) of the thermodynamic systems under consideration, and they are connected by the equation G = H –TS, where H is a further thermodynamic function called enthalpy.
Ideal gases mix spontaneously in all proportions. This means that for any possible composition, the entropy of mixing (∆mixS) is positive, and the Gibbs free energy of mixing (∆mixG) is negative. If there are no interactions between the molecules, no heat is generated or consumed by the process and the enthalpy of mixing (∆mixH) will be zero.
The ideal solution is just like the mixture of two ideal gases, the only difference being that the components are in the condensed phase. Therefore, all the equations obtained for the ideal gas hold: the driving force for mixing is the increasing entropy of the system as the molecules mingle and the enthalpy of mixing is zero. Although the terminology for ideal/real solutions is the same as for gases, there is an important difference:
It should be noted, however, that solution ideality means something different from gas perfection. In a perfect gas there are no forces acting between molecules. In ideal solutions there are interactions, but the average energy of A-B interactions in the mixture is the same as the average energy of A-A and B-B interactions in the pure liquids. […] It is on the basis of this distinction that the term ‘perfect gas’ is preferable to the more common ‘ideal gas’ [p. 149].
From a philosophical point of view, however, the basis of solution ideality is the same as the basis for gas perfection, namely, the lack of interaction between constituting parts (between gas molecules, and between liquids A and B, respectively). Not only is the basis of ideality the same as with ideal gases, but its status is similarly valorized as well. If real gases are treated as imperfect copies of the ideal gas, then real solutions are treated as imperfect copies of the ideal solution. The section "The properties of solutions" (pp. 148-58) is the mirror of the chapter "The properties of gases": it starts with ideal solutions, and then discusses "the deviations from ideal behaviour exhibited by real solutions" (p. 148).
Real solutions are composed of particles for which A-A, A-B, and B-B interactions are all different. Not only may there be enthalpy and volume changes when liquids mix, but there may also be an additional contribution to the entropy arising from the way in which the molecules of one type might cluster together instead of mingling freely with the others [p. 149].
As a result, the Gibbs free energy of mixing may be positive, in which case separation is spontaneous and the liquids are immiscible, or miscible only over a certain range of compositions.
If in the gas case, non-ideality was represented by the compression factor Z, and by the van der Waals constants a and b, then non-ideality of solutions is mathematically represented by the so-called excess functions. An excess function is the difference between the observed thermodynamic function of mixing and the function for an ideal solution, which in turn is the same as for a mixture of ideal gases.
The excess entropy of mixing (SE) is defined as follows (p. 149, equation 5.29):
SE = ∆mixS – ∆mixSideal
where ∆mixS is the entropy of mixing for the real mixture, and ∆mixSideal is the entropy of mixing for the ideal mixture. The same pertains to H and G.[7]
The possibility of being non-ideal on more than one account introduces a further gradation on the scale of perfection-imperfection: mixtures with zero excess entropy and non-zero excess enthalpy are called "regular solutions" (ibid.). This model system is afflicted by one source of non-ideality, but not with the other: the two kinds of molecules are distributed randomly, as they would be in an ideal solution (hence, the entropy of mixing has its ideal value), but have different energies of interaction with each other, which results in an enthalpy change when mixing them.
Another similarity between the description of gases and solutions is expressed in the concepts of fugacity and activity. Let me explain the concept of activity first. In the ideal solution, solute molecules behave as if each of them was alone in the solution. In real solutions, however, the molecules hinder each other’s participation in processes. The mechanism of this effect is not discussed; instead, its consequences are congealed into the so-called ‘activity coefficient’. The activity coefficient is the ratio of the activity of the substance to its concentration.
The concept of activity, the effective concentration of the solute, has its counterpart in the concept of fugacity, the effective pressure of a gas.[8] Activity and fugacity are designed to deal with solution non-ideality and gas imperfection. The point of the whole exercise is that the equations of state obtained for ideal systems remain valid for real systems; all we need to do is to replace concentration with activity and pressure with fugacity. Atkins puts this as follows:
In Chapter 3 […] we remarked that a quantity called ‘fugacity’ takes into account the effects of gas imperfections in a manner that resulted in the least upset of the form of equations. Here we see how the expressions encountered in the treatment of ideal solutions can also be preserved almost intact by introducing the concept of ‘activity’ [p. 158].
Although it looks as if the problems of solution non-ideality and gas imperfection have been solved, they simply have been given another name, i.e., activity and fugacity coefficients, respectively. The difficulty is that the coefficients are to be determined empirically; apart from postulating their existence, and that they emerge as the consequence of interactions, the theory does not say anything more about them. As with the excess functions and compression factors, solution non-ideality and gas imperfection are congealed into empirical constants. The fact that the constants have to be obtained empirically indicates that the effects they stand for lie outside the bounds of the theory. To account for them theoretically would mean to explain them with reference to some underlying causes in a quantitative fashion. One should be able to calculate the actual values of the coefficients from more fundamental characteristics of the molecular entities, rather than having to measure them.
4. Philosophical ideas in the thermodynamic description of gases and liquids
There are three sets of culturally valenced metaphysical ideas embedded in the thermodynamic description of gases, liquids, and mixtures thereof. First, postulating the existence of an ideal gas or solution, as distinct from real gases or solutions, is a form of platonism, i.e., the valorization of an ideal type over its actual manifestations. Second, there is a scale of perfection-imperfection on which states of matter are positioned, with the ideal gas on the top, real gases in the middle, and liquids at the bottom. The same hierarchy is evident in the ideal solution/regular solution/real solution sequence. The first and second topics are related, for without the ideal type, the ranking of various states of matter would not be possible; they are ranked on the basis of their (dis)similarity to the ideal type. Finally, we must pay attention to the content of the idealization and ask: which features of real thermodynamic systems are regarded as essential and thus part of the model and which are treated as of secondary importance? Ultimately, the scale of perfection/imperfection is a function of the intermolecular forces in the system and of the extension of the molecular entities in space, i.e., their embodiment. Interactions and embodiment are seen as problems, as deviations from the ideal state. This makes the thermodynamic theory of gases and solutions akin to liberal political theory, in that both place great emphasis on atomism/individualism and disembodiment. Let me explore these issues in more detail.
4.1 Platonic idealism
Platonism is the view that particular objects, properties, and relations are imperfect copies of some archetypical abstract entities, the forms or ideas.[9] Although Platonic idealism originates with Plato, platonism (in lower case) is also a contemporary view in metaphysics and there are historical as well as contemporary alternatives to it. In contemporary analytic metaphysics, the issue at hand is known as the problem of universals. Most philosophers agree that particulars (physical objects) exist, but the ontological status of universals (properties, relations and kinds) is disputed. Similarly, the ontological status of laws and theoretical entities is disputed in general philosophy of science. The possible viewpoints cluster around three stances.
(1) The first is Platonic idealism, which has its source in Plato’s theory of forms. The forms, according to Plato, are archetypes (original models) of which particular objects, properties, and relations are copies. The forms are abstract entities existing outside space and time; they are therefore more perfect than material things which are subject to change and decay. Not only are material things imperfect instantiations of the eternal forms; they acquire their very existence and identity through partaking in the form in question. What makes X an X is its relation to the form of Xness; the form is its essence so to speak. Particular things depend for their identity and existence on the forms, but the forms do not depend on particular things for the same. In other words, universals exist ‘ante rem’, that is, prior to and independently from particulars.
(2) Aristotle shared with Plato the view that things must have some fixed essence; otherwise we would not be able to either identify or to know them.[10] As opposed to Plato, however, he thought that universals are immanent properties existing only in concrete material things, but not independently of them. This position is usually referred to as ‘in re’ realism about universals (Rodriguez-Pereyra 2011). The ontological priority given to ideas, by Plato, and to concrete things, by Aristotle, is clearly a matter of value judgment as well; both views are equally compatible with whatever experience one can ever have about the world.
(3) The third position is nominalism, which maintains that universals do not exist at all. An interesting articulation of this view for the philosophy of science is to be found in Cartwright (1983).
Cartwright’s argument is against the traditional interpretation of the laws of nature and of scientific explanation in the philosophy of science, i.e., the deductive-nomological model. This model holds that science explains particular events through subsuming them, or certain aspects of them, under general laws of nature. But explanation, Cartwright argues, has a causal aspect to it; if laws do in fact explain events, they must be understood as the causes of those events; they prescribe what should happen in nature (Cartwright 2005, p. 1).
Cartwright rejects this view on logical as well as on empiricist grounds. Logically speaking, if laws are non-spatiotemporal abstract objects, as the Platonic forms are, they are then also causally inert and cannot be the causes of anything that happens in the material world (ibid., pp. 10-4).[11] Further, the view that abstractions should have a more fundamental existence than concrete material things is incompatible with an empiricist epistemology. Cartwright goes a bit further than is necessary to refute the Platonic understanding of the laws of nature; instead of adopting view 2, she concludes that there are no laws of nature at all.
On Cartwright’s account, the choice is between Platonic laws or no laws at all. I think however that one does not need to attribute transcendent causal power to the laws of nature to be able to say that they exist. Laws can be thought of as merely describing, rather than prescribing regularities; they explain natural processes with reference to some common feature of the material systems for which the laws hold. Causal agency lies with this particular feature, present in each system, rather than with the proposition that states its existence.
For Cartwright, the extent to which the laws of physics ‘lie’ is a function of their remoteness from experimentation. She sees more truth in facts (measurements) than in phenomenological laws, in phenomenological laws than in theoretical laws, in the laws of the applied sciences than in the laws of physics, and in laws acting separately than in laws acting in combination. This seems to be the legacy of the origins of philosophy of science in logical positivism, which rejects anything that is not firmly grounded in sense experience as metaphysical speculation. Regularities, relations, kinds, causes, etc. are not directly observable; they must be inferred to through comparison, abstraction, and generalization. Therefore, they can not be said to exist in a strictly empiricist framework.
In short, the first view outlined above holds that things do have some essence, and the essence is transcendent (objective idealism). The second view holds that things do have an essence, but this essence is immanent (materialism). The third view holds that there is no essence at all (subjective idealism).[12]
The third position is clearly incongruous with the scientific attitude, as are Cartwright’s conclusions. For if there are no universals, no regularities in the world and no laws of nature, what is then science about? The first and the second positions agree that there are regularities in nature, which can be summarized in the form of models, theories, theoretical entities, and so on. They differ, however, in the ontological status granted to these abstractions. In the Platonic view, some essence is postulated irrespective of whether and to which extent any particular thing resembles it. In the Aristotelian view, the essence is identified by mentally abstracting the properties that all instantiations share.
What is the essence of a gas? In Atkins’ textbook, a gas is defined with reference to an essential property, namely, filling all the space available. "The simplest state of matter is a gas, a form of matter that fills any container it occupies" (p. 3). This is what makes a gas a gas. Filling the space available is specific to the gas state; for a given pressure and temperature, liquids and solids have a fixed volume and do not occupy all the space available to them.
It is, however, precisely this aspect where real gases deviate from the ideal gas. Theoretically speaking, filling the space available means that a gas can expand or contract to whatever extent, and that the pressure-volume product at any given temperature is constant for all volumes and pressures. Real gases do not behave in this way. The departure from ideal behavior is expressed quantitatively in the compression factor (Z). The compression factor is the ratio of the molar volume of the gas to the molar volume of the ideal gas under the same conditions. As Figure 1 shows, for medium pressures, Z is smaller than 1 for most real gases because the attractive forces hold the gas molecules together, preventing them from expanding to the extent predicted by the ideal gas law. At high pressures (> 200 atmosphere) the molecules are pushed closer together, the repulsive forces become dominant and the gas occupies a bigger volume than the ideal gas would. Not only is there a substance-specific compression factor for each type of gas; it also varies with the pressure. Real gases differ from the ideal gas precisely in the aspect that is said to be their essence, that is, their propensity to fill the space available to them.
Importantly, platonism in the treatment of gases and solutions stems from the inability of the theory to deal with interaction and embodiment. The theory wishes to disregard interactions and constructs ideal systems free of interaction, while at the same time declaring that in real systems, interactions cannot be disregarded. This declaration is implicit in the constraints that are set on the validity of these approximations. The ideal gas equation is a limiting law; real gases conform to it increasingly as the pressure approaches zero. Thus real gases behave as an ideal gas at zero pressure, when no gas molecule is present. The same idea operates in the thermodynamics of solutions: real solutions exhibit ideal behavior as the concentration of the solute approaches zero, that is, when no solute molecule is present in the solvent (in which case it is not a solution but a pure liquid). The models offered for gases and solutions are thus incapable of conceptualizing something that is essential to all actual occurrences of the phenomena they seek to describe. Something that is not characteristic of all cases is postulated as their essence; something that is characteristic of all (namely, intermolecular forces) is treated as of secondary importance.
One might well ask at this point whether we could regard the ideal gas as a boundary case that helps us understand the more complicated real gases, rather than seeing it as a Platonic ideal type. If so, this could be a typical case of idealization in science, whereby various factors involved in the same process or phenomenon are conceptually and/or experimentally separated, investigated in isolation, and finally combined, so as to achieve a complete understanding of all factors and how they act in combination.[13] But this is precisely what is missing here.
There are two phenomena to discuss with respect to the gas state: the motion of individual gas molecules and the interactions between them. There is an asymmetry in the way the two issues are treated by the theory. The first issue is dealt with in a theoretical fashion, while the second is accounted for in terms of empirical constants only, such as the compression factor and the van der Waals and fugacity coefficients. Empirical constants are ad hoc adjustments of facts to equations, and they signify the inability of the theory to tackle the underlying phenomena.
Here is another way to put it: The ideal gas law provides a phenomenological description of how the physical properties of gases (p, T, V, and n) are related to each other. The kinetic model of gases provides a conceptualization of the underlying microstructure of matter that explains this law. However, the phenomenological description, to which the model is fitted, is accurate for a narrow range of temperature and pressure only. There is no model offered to quantitatively explain the behavior of gases in other T-p regions. Instead, the ideal gas law is amended by empirical constants, which are a measure of the non-ideality of real substances. The coefficients are not the consequence of the theory as applied to certain non-ideal substances; rather, they are a measure of how the theory does not apply to them. Real gases resemble the ideal gas, except when they do not, and the only thing we can do about the misfit is to measure it.
4.2 Hierarchy of states of matter
In the ideal gas model, the ideal gas serves as a reference point and real gases are characterized in terms of their conformation to or deviation from ideal behavior. The factor preventing real gases from behaving ideally is the presence of intermolecular forces, the effect of which is small at low pressures and high temperatures only. As the pressure increases – while the temperature is held constant – the molecules are pressed closer to each other, interactions become more significant, and the gas increasingly deviates from ideal behavior until it liquefies. Intermolecular forces are significant in real gases, and even more significant in the liquid and solid states. Now if the ideal gas is the perfect form of matter because there are no interactions between its molecules, then the real gas is a less perfect form, the liquid, even less, and the solid must be the worst.
The hierarchical ordering of physical states is expressed not only by value-laden terms, such as ‘imperfection’, ‘non-ideality’ and ‘deviation’, but also by the very structure of the theory. In the process of constructing the equation of state for real gases, the point of departure is the equation of state of an ideal gas. This equation needs to be modified so as to incorporate some terms which express the contribution of intermolecular forces to the pressure. This results in the virial, van der Waals, Berthelot, and Dieterici equations of state. The perfect gas equation becomes mathematically more complicated when interactions are taken into account. If intermolecular forces are represented as a cause for ‘imperfection’ on the linguistic level, they appear as complications on the mathematical level.
We might well imagine an alternative theory which starts out theorizing interrelationships among molecules, derives quantitative relationships between the physical properties that determine the possibility of such interaction, and finally, constructs the state of gases at low pressure as an exceptional and atypical case where the effect of interactions vanishes. In this alternative theory, it is the free motion of the gas molecules that would require explanation and which would be treated as an addendum causing complications in the mathematical apparatus. In the theory we now have, real gases seem complicated because some of their characteristics (intermolecular forces and the non-zero volume of the molecules) are not part of the original model, and not the other way round.
Let us now consider condensed phases, i.e., the liquid and solid states. Surprisingly, although phase transitions are of central importance to chemists, and the textbook does devote considerable space to discuss them (pp. 117-35, 174-99), condensed phases are neither defined nor explained in the same manner as the gas state. The chemical thermodynamics section of the textbook does not offer any characterization of the structure of liquids or solids.[14] On page 144, we find a figure with the subtitle "A pictorial representation of the molecular basis of Raoult’s law" (Figure 2).

Figure 2: "A pictorial representation of the molecular basis of Raoult’s law. The large spheres represent solvent molecules […], and the small spheres are solute molecules". Source: Atkins & de Paula 2006, p. 144, Fig. 5.13, by permission of Oxford University Press.
This picture illustrates how solutions and liquids are imagined in chemical thermodynamics. Although the title speaks about molecules (molecules consist of atoms and so they have a structure), the picture shows rigid impenetrable spheres with no inner structure, as if they were billiard balls. The billiard ball simile, which originates with the kinetic theory of gases, is thus extended from the gas to the liquid state. The liquid is imagined exactly as the perfect gas, the only difference being that the balls are closer to each other. It is the interrelationships between molecules that makes a liquid a liquid, and without molecular structure, such relationships are not imaginable. Yet on the picture, the solvent (which for sure is a liquid, although the solute might not be) is depicted as a set of billiard balls without specific shape and structure. The liquid state is modeled on the gas state and the gas state is modeled on the fictitious ideal gas.
It is at this point that we can fully assess the consequences of the negligence of interactions. As regards gases, one could argue that they are indeed free to fill the space available to them, although constrained by interactions. Therefore, either the motion of individual particles or the interactions among them could be a legitimate starting point for a theory. Liquids, however, never come without interactions, and yet their properties are described in terms of deviations from a model whose validity depends on the lack of interactions.
4.3 Atomism/individualism and disembodiment
Apart from diagnosing Platonic idealism in the theory, that is, the postulation of the existence of an ideal type and imperfect copies thereof, it is equally important to ask: what makes the ideal type ideal? Which properties of real gases are considered essential, thus part of the ideal type, and which are disregarded as epiphenomenal, contingent, and secondary? What values motivate the choice?
Classical or phenomenological thermodynamics, developed in the first half of the 19th century, postulates laws that specify the relationship between various forms of energy, but it does so without reference to the underlying structure of matter. It was only in the second half of the same century that the phenomenological laws were given a molecular interpretation (Brush 1976). The processes that are thought to take place on the molecular level are described with the help of Newtonian mechanics.
The ideal gas model in chemical thermodynamics rests on the kinetic theory of gases, which is a mechanical model. It describes a gas as a large number of rapidly moving, small particles that frequently collide with each other and with the wall of the container. The particles are imagined as hard spheres with no inner structure, like billiard balls. Macroscopic properties of the gas (such as volume, temperature, and pressure) are explained with reference to molecular motion. This motion is described in purely mechanical terms: all interactions are mechanical and no energy comes from non-mechanical interactions, e.g., attractive or repulsive forces.
The treatment of molecular entities in the kinetic theory of gases resembles the treatment of individuals in liberal political theory. Liberalism conceives of society as a set of autonomous individuals; in the kinetic theory of gases, gas is conceived of as a set of independent particles. In both cases, properties of the system are derived from the properties of its parts in an additive fashion, rather than in terms of interactions or relations between those parts.
Apart from individualism, another feature that makes the ideal gas model akin to liberal political theory is its conceptualization of the gas molecules as material points without extension and inner structure, a feature that I have called disembodiment. Liberal thought defines human beings in terms of their capacity for reason, a faculty which is thought to operate independently from the material, historical, social, and cultural context this human being finds herself in. To think of society as a collection of individuals is to strip these individuals from the social context they live in; to think of these individuals as the carriers of disembodied reason is to strip this rationality from the biological context that makes it possible. Both individualism and disembodiment result in decontextualization.
Atomism and disembodiment are interrelated in chemical theory as well. The intermolecular forces that are omitted from the treatment of ideal gases are attractive and repulsive forces that are electrostatic in nature, and can only arise between permanent or induced dipoles. Polarization is the consequence of the non-uniform distribution of positive and negative charges on the various atoms that constitute the molecule. The particles need to be thought of as bodies with an extension in space and with an inner structure before any non-mechanical interactions among them can be postulated.
The parallelism between liberalism and the corpuscular theory of matter can be analyzed either philosophically, through pointing out the similarity of structure in the two theories, or historically, through exploring the various ways in which scientific concept formation is informed by political ideas and cultural values evident in non-scientific discourses of the same era. I have tried to point out the parallelism with the help of conceptual analysis, but my claims are supported by the history of science as well.
Modern science developed in the context of the English Revolution, which brought about the downfall of feudalism and the rise of capitalism, accompanied by the demolition of the absolute monarchy and the establishment of the political institutions of the new bourgeois class. Liberalism was the ideology of the latter; its demands for political liberties "expressed the challenge of the rising merchant and later the industrial capitalist class against the restrictions on travel, finance, and manufacture by which the feudal system hampered the growth of trade and industry" (Jaggar 1983, p. 27). While social and political philosophies served as the ideological underpinnings of economic and social change, they also served as an inspiration for natural philosophers (scientists). The social meaning of scientific ideas played an important role in the integration of the new science into Western culture (Jacob 1988). Freudenthal (1986) argued that the concepts of element and system in 17th century natural philosophy (Bacon, Descartes, Newton, and Boyle) mirrored the conceptualizations of individual and society in the political and social philosophies of the era. Freudenthal also pointed out the congruence between the bourgeois individual and the essential properties of a particle in Newton’s thought in particular.
In short, the individualism of liberal political theory is reflected in the atomism of the corpuscular philosophy that underlies Newtonian mechanics, and which is the conceptual foundation of the kinetic theory of gases. In both cases, the ontologically primary entity is the individual particle or person, whose essential quality is freedom, understood as independence from other parts of the system and facilitated by the disembodied nature of the element.[15] The ideal gas particle is the modern individual in bourgeois society.
5. Metaphysical principles, cultural values, and gender ideology
Having analyzed the thermodynamic theory of gases and solutions for the philosophical ideas they contain, I would now like to put forward some arguments as to why any of these should be seen as a feminist issue or as a case of gender bias (gender ideology) in science.
5.1 Platonism and the problem of essentialism in feminist thought
Several commentators of Plato pointed out that his views were deeply inegalitarian. Elizabeth Spelman argued that the hierarchical thinking found in Plato’s political philosophy is not unrelated to his metaphysics, that it, the theory of forms. In her Inessential Woman (1988), Spelman focuses on the diversity of women and the problems of exclusion in feminist thought. Second-wave feminist theorists claimed that in Western culture, women were always thought of as inferior and less human as compared to men because the very ideals of humanness were (and are) modeled on men. In a similar fashion, theorists of the third wave of the women’s movement accused their second-wave predecessors of having elevated the experiences of white, Western, heterosexual, middle-class women to a universal status, thereby marginalizing and excluding less privileged women.
Spelman argues that the problem with both the masculinist and the second-wave feminist accounts is that they think about humans or women in an essentialist way. Postulating that an entity has some sort of essence results in erasing heterogeneity among the members of this group. As long as we suppose the existence of ideal forms – as Plato’s theory of forms does – we risk modeling those forms on a certain group of people or things, thereby excluding and devaluing others. In short, Spelman traces back the ethnocentrism, classism and heteronormativity of second-wave feminist theory to its essentialism.
By now the position advocated by Spelman has become predominant in feminist theory. Postmodern feminist thinkers claim that the search for common features in the situations of women or in women themselves is both metaphysically wrong and politically undesirable. Traditional categories of social and cultural analysis (sex, gender, race, ethnicity, identity, etc.) have all been deconstructed and rejected on this ground. The typical genre in gender studies (and in a vast array of other ‘studies’ in contemporary academia) is the case study with its emphasis on and celebration of the uniqueness and complexity of particular situations. One cannot ask, without inviting charges of naivety, backwardness, or theoretical unsophistication: what are they cases of? "The world is a confused conglomeration of special cases"[16] of which nothing common can be postulated (sometimes perhaps analogies between cases are allowed to draw, but not in a systematic fashion). This view is identical with the nominalist view outlined in section 4.1. As in Spelman and in Cartwright, it is typically articulated with reference to the platonist view, and it is motivated by the rejection of that view.
I think however that this position (view 3) is inadequate for the philosophy of science and for feminist theory, for roughly the same reason. Denying the existence of regularities in nature or in society renders natural science and social science impossible or meaningless. Knowing the world is a prerequisite for any attempt to change it. If there were really nothing common to all women, we would not know who the women are. If there is nothing common in the situations women find themselves in, there can be no feminism.[17] The problem with the prominent figures of second-wave feminist theory is not that they postulated some kind of essence of womanhood, but rather, that they abstracted this essence from the lives of white, middle-class, heterosexual women. As in the ideal gas model, the problem is not with generalization per se, but rather with the misfit between the basis of generalization and the intended scope of its validity.
My argument, in the context of natural science and feminist theory, is for position 2, where the essence emerges as the theoretical content of all the particular cases of which it is postulated. Contrary to Aristotle, however, I think that the essence is not a fixed thing but something that changes over time, although not with the same speed for each being. So for example the nature of gases is the same today as it was in the 19th century, while the nature of women is clearly not. In the second part of this paper (Kovács 2012), I shall argue that the philosophical legacy of Georg Lukács provides ground for such a viewpoint.
5.2 Ontological heterogeneity as a feminist virtue
In a series of publications, Longino proposed six criteria which can serve as feminist standards for evaluating scientific theories (Longino 1992, 1995, 1997). She distilled the ‘feminist virtues’ from the feminist critique of the life sciences, identifying broader philosophical issues behind the particular features of the biological theories the feminist criticism was leveled at.
The feminist virtues are heterogeneous in nature. Empirical adequacy and novelty are formal traits of theories; complexity of relationship and ontological heterogeneity are substantial metaphysical assumptions, while alleviation of human needs and the decentralization of power through the applications of knowledge and technologies are practical considerations (Longino 1992, p. 336). My interest is in the metaphysical assumptions and how the values evident in the ideal gas model can be mapped onto them.
Ontological heterogeneity and complexity of relationship express the same values, one in relation to entities, and the other, in relation to the processes in which the latter take part. It is the first notion that is relevant to my analysis of the model of the ideal gas.
According to Longino, a feminist theory should take account of individual difference among the individuals and samples that constitute the objects of study, rather than erasing that difference or subsuming it under general categories. Feminist theorists reject "theories of inferiority" because
Theories of inferiority which take the white middle class male (or the free male citizen) as the standard grant ontological priority to that type. Difference is then treated as a departure from, a failure to fully meet, the standard, rather than simply difference. Ontological heterogeneity permits equal standing for different types, and mandates investigation of the details of such difference [Longino 1992, p. 337].
In chemical thermodynamics as presented in Atkins’ book, the perfect/ideal gas is a theoretical construct, an idealized version of a gas. Real gases resemble the ideal gas under certain conditions only, such as low pressure and high temperature, which guarantee the negligibility of interactions between the molecules. As these conditions change, the real gas increasingly deviates from ideal behavior until it liquefies. When the gas condenses, "all similarity to perfect behaviour is lost" (Atkins & de Paula 2006, p. 17) and the limit in the intensive parameters (pressure and temperature) which constrain the possibility of such a transformation are called "critical constants" (ibid.). Clearly, forms of matter are understood here as stages on a scale of perfection-imperfection, with the perfect gas on the top, real/actual gases in the middle, and liquids at the bottom. The perfect gas is the standard to which other forms of matter are compared. The hierarchy of states of matter is based on the extent to which these states resemble the ideal gas. Thus the theory of matter in Atkins is a theory of inferiority.
5.3 The gender dimensions of individualism and disembodiment
I have argued, in Section 4.3, that the ideal gas model in chemical thermodynamics is analogous to the liberal conception of society. The two models are similar in two respects. First, both put an excessive emphasis on the properties of the parts at the cost of undertheorizing the relationships between them (atomism/individualism). Second, liberal political theory conceives of individuals as disembodied minds, while the ideal gas model conceives of gas particles as material points without extension in space (disembodiment).
Alison Jaggar pointed out that the basic tenets of liberal political theory are male-biased (1983, pp. 39-48). First, liberalism defines human beings in terms of their capacity for rational thinking and thus identifies them with disembodied reason. The mind-body dualism is a recurring topic in Western philosophy and it usually comes with what Spelman called "psychophylic somatophobia", or excessive love of the mind and hatred of the body (1982, p. 119).[18] The problem with the celebration of the mind over the body is that it exists next to an equally long-standing tradition of associating women’s nature and women’s lives with the body, in philosophy as well as in popular culture (Bordo 1993). The cultural association of women with body and men with mind
has been reinforced if not generated by a sexual division of labor in which (some) men have dominated the ‘intellectual’ fields of politics, science, culture and religion, while women have been assigned the primary responsibility for many day-to-day tasks necessary for physical survival, tasks which include food preparation, psychological nurturance and the care of infants and young children [Jaggar 1983, p. 46].
Arguably, the negligence of the embodied aspects of human existence is one of the reasons why liberalism could not provide adequate grounds for the liberation of women. For although liberalism declares that each and every individual should have certain rights and freedoms, these rights are in fact not universalizable, as their attainability for some depends on their unattainability for others. A division of labor analysis, such as Jaggar’s, shows that the freedom of some from the bodily dimensions of human life is contingent on others taking care of them. An analysis of culture in a psychoanalytic fashion shows that the liberal ideals of epistemic authority and personhood can be attained only through the splitting off and denial of aspects of the self (such as embodiment) which then must be projected onto women and other underprivileged groups, who are therefore bound to appear less rational and less human (Scheman 1996; Bordo 1987, pp. 97-118).
The individualism of liberal thought has been subject to Marxist critique for reasons that have their counterparts in feminist theory. Rather than seeing society as a collection of autonomous individuals, historical materialism defines human nature as the totality of social relations. There is a parallel argument in feminist thought regarding the importance of starting analysis from social relations rather than from individuals. Socially conservative discourses explain gender difference with reference to traits inherent in men and women. The major achievement of feminist theory was to reconceptualize gender as a process, that is, the social production of gendered subjects, their distribution into unequal relationships and the construction of cultural representations that make all of this seem natural. There is a similarity between the structure of explanation in the Marxist theory of society and in feminist theories of gender in that both derive the characteristics of individuals from the properties of the social system, rather than vice versa. Marxist philosophy developed the concept of reification to refer to thought processes whereby features of social relations are attributed to objects. On a more abstract level, this amounts to focusing on things as opposed to processes and relations. This is the explanatory strategy employed in the kinetic theory of gases.
6. Conclusions
I have argued that the model of the perfect gas is built on philosophical assumptions (platonism, a hierarchy postulated among various states of matter, disregard for embodiment, and individualism) that have been problematized by feminist scholarship. Pointing out that some piece of science is value-laden invites the question: could there be alternatives to it? Could there be a feminist chemical thermodynamics?
Creating feminist chemistry or feminist chemical thermodynamics in detail would be a scientific project which I cannot pursue here, but my analysis provides some ground for an outline of the philosophical principles this theory would utilize. Such a theory would take interaction and embodiment as basic features of all forms of matter. Because these do in fact characterize all known substances, it would be impossible to devalue any particular form of matter on the basis of its non-compliance with the ideal type. In other words, there could be no hierarchy postulated among them.
My aim with this analysis is not to prescribe what direction the development of chemical theory should take or should have taken, but rather, to arrive at a better understanding of the cultural embeddedness and ideological content of the currently accepted theory. Pointing out that there could be, at least in principle, alternatives to it helps to take its basic metaphysical commitments for what they are, i.e., the applications of philosophical ideas or worldview elements in the scientific context.
Underlying my analysis of the model of the ideal gas is an epistemological perspective, according to which the theories of the physical sciences necessarily rely on such worldview elements, which designate the locus of social ideologies in these theories. I develop this theoretical perspective in the second part of the paper (Kovács 2012).
Acknowledgements
Talks that included various parts of this article were presented at the 7th European Feminist Research Conference in June 2009, Utrecht, Netherlands; at the 7th International Conference on the History of Chemistry in August 2009, Sopron, Hungary; and at the Conference of the International Association of Women Philosophers in June 2010, London, Ontario, Canada. I am grateful to members of these audiences for constructive criticism and encouragement.
I am grateful to two anonymous referees, Anna Leuschner, and Joachim Schummer for helpful suggestions on an earlier draft. I thank Helen Longino for numerous conversations which significantly improved my thinking about the epistemological dimensions of feminist science criticism and refined my understanding of her work. I thank László Ropolyi for careful reading and valuable comments on several drafts and the final revision, as well as for many years of discussion which have been essential to my understanding of philosophy, thermodynamics, and the relationship between the two.
The research for this article was partly supported by the Central European University Foundation, Budapest (CEUBPF). The views expressed in this publication do not necessarily reflect the opinions of CEUBPF.
Notes
[1] For an analysis of the first and second laws of thermodynamics, and the comparison of the mechanistic and thermodynamic paradigms in the same fashion, see Kovács (forthcoming).
[2] My analysis is based on the 8th edition; the 9th one came out while I was working on this study.
[3] All subsequent page numbers refer to this textbook unless indicated otherwise.
[4] Atkins prefers the term ‘perfect gas’ to the more widely used ‘ideal gas’, for reasons to which I come back later in this essay. I use the two terms interchangeably.
[5] Understandably, the textbook does not perform this construction of equations from experimental data, which, in the case of the ideal gas law, was a matter of two centuries of scientific work.
[6] An elastic collision is a collision in which the total translational kinetic energy of the colliding molecules is preserved.
[7] The entropy of mixing is always positive, even in the ideal case, whereas the enthalpy of mixing is zero for ideal mixtures.
[8] Fugacity (f or F ) and the compression factor (Z) are different measures of gas imperfection. They are connected by the equation (Atkins & de Paula 2006, p. 112, equation 3.60): 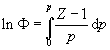
[9] My understanding of platonism is indebted to Gill 2006 and Balaguer 2009.
[10] My reading of Aristotle’s Metaphysics is informed by Politis 2004, pp. 295-330 and Ross 2004, pp. 161-94.
[11] For these reasons, Cartwright renounces the notion of laws of nature and puts faith in theoretical entities as the causes of events instead (1983, pp. 91-9). In this I believe she is mistaken. For both in quantum mechanics (the field from where she gives examples) and in thermodynamics (the topic of this paper), something which is a theoretical entity in one interpretation of the theory is a law in another interpretation. For example, the electron, a theoretical entity in whose existence Cartwright does believe, is a particle in some contexts and a wave in others. The analogy with mechanical waves, which makes it possible to describe the quantum state of particles with wave functions, as well as the wave equations themselves, are laws of nature.
[12] In analytic metaphysics, the three positions with respect to universals are called platonism, immanent realism, and nominalism (Balaguer 2009). These correspond to the more general philosophical positions of objective idealism, materialism, and subjective idealism, understood as follows. Materialism holds that the only thing that exists is matter, while idealism postulates the existence of mind or spirit that is underivable from material interactions. This terminology, developed by Engels (1886/1949) highlights the ideological significance of the issue at hand, i.e., whether the world is knowable via the faculty of sense perception. Only the second position answers this question in the affirmative. Platonists have difficulties explaining how humans who exist within spacetime can aquire knowledge of abstract objects existing outside of it. For the subjective idealist, sensory perception of concrete states of affairs is possible, but any generalization over and above them, sometimes even inference to the existence of the outside world, is problematic. For an analysis of subjective idealist tendencies in positivism, see Lenin 1908/47.
[13] For a description and defense of this typical element of scientific methodology, see McMullin 1985.
[14] There are theories elsewhere in physical chemistry that deal with the structure of liquids, such as the Debye-Hückel theory of electrolyte solutions. However, the Debye-Hückel theory seeks to explain departures from solution ideality, thus leaving the conceptual primacy of ideal solutions unchallenged.
[15] The analogy between the ideal gas particle and the liberal conception of the modern individual is strengthened by metaphors of freedom in the scientific theory. Freedom is the chief value in liberalism; in fact, the very name of liberalism is derived from liberty. In chemical thermodynamics, gas is defined as the state of matter which fills any container it occupies; the molecular entities are free to roam all around the space available to them, unless constrained by interactions.
[16] Not insignificantly, these are the words Simone de Beauvoir uses to depict the viewpoint of women, which she contrasts with scientific thinking (Beauvoir 1953, p. 580, cited in Spelman 1988, p. 202).
[17] For a more sophisticated argument as to why gender essentialism is not necessarily incompatible with a social and historical understanding of gender, see Witt 2011.
[18] Spelman also points out how the higher worth and importance of the soul in comparison to the body is reflected in the supremacy of the invisible eternal world of the forms over the material, changing world of appearance in Plato’s thought.
References
Atkins, P.W. & de Paula, J.: 2006, Atkins’ Physical Chemistry, 8th ed., Oxford: Oxford University Press.
Balaguer, M.: 2009, ‘Platonism in Metaphysics’, in: E.N. Zalta (ed.), The Stanford Encyclopedia of Philosophy (Summer 2009 Edition) [online at: http://plato.stanford.edu/archives/sum2009/entries/platonism/].
Beauvoir, S.: 1953, The Second Sex, trans. by H.M. Parshley, New York, Knopf.
Bleier, R.: 1984, Science and Gender: A Critique of Biology and its Theories on Women, New York: Pergamon Press.
Bordo, S.: 1987, Unbearable Weight: Feminism, Western Culture, and the Body, Berkeley; University of California Press.
Bordo, S.: 1993, The Flight to Objectivity: Essays on Cartesianism and Culture, Albany: State University of New York Press.
Brush, S.G.: 1976, The Kind of Motion We Call Heat: A History of the Kinetic Theory of Gases in the Nineteenth Century, Amsterdam: North Holland.
Cartwright, N.: 1983, How the Laws of Physics Lie, Oxford: Clarendon Press.
Cartwright, N.: 2005, ‘No God, No Laws’, unpublished manuscript [online at: http://www.isnature.org/Files/Cartwright_No_God_No_Laws_draft.pdf, accessed on 21 March 2012].
Engels, F.: 1886/1949, Ludwig Feuerbach and the End of Classical German Philosophy, Moscow: Foreign Languages Publishing House.
Fausto-Sterling, A.: 1992, Myths of Gender: Biological Theories about Women and Men, 2nd ed., New York: Basic Books.
Freudenthal, G.: 1986, Atom and Individual in the Age of Newton: On the Genesis of the Mechanistic World View. Dordrecht & Boston: D. Reidel.
Gill, M.L.: 2006, ‘Problems for Forms’, in: H.H. Benson (ed.), A Companion to Plato, Malden, MA: Blackwell, pp. 184-98.
Gowaty, P.A.: 2003, ‘Sexual Natures: How Feminism Changed Evolutionary Biology’, Signs, 28, 901-21.
Haraway, D.J.: 1989, Primate Visions: Gender, Race, and Nature in the World of Modern Science, New York: Routledge.
Hubbard, R.: 1990, The Politics of Women’s Biology, New Brunswick: Rutgers University Press.
Jacob, M.C: 1988, The Cultural Meaning of the Scientific Revolution, New York: Alfred A. Knopf.
Jaggar, A.M: 1983, Feminist Politics and Human Nature, Totowa: Rowman & Allanheld.
Keller, E.F.: 1992, Secrets of Life, Secrets of Death: Essays on Language, Gender, and Science, New York: Routledge.
Kovács, Á.: 2012, ‘Gender in the Substance of Chemistry, Part 2: An Agenda for Theory’, Hyle: International Journal for Philosophy of Chemistry, 18 (2), 121-43.
Kovács, Á.: forthcoming, ‘Gender in Chemical Thermodynamics: Metaphors and Worldviews in Atkins’ Physical Chemistry’, in: H. Götschel (ed.), Transforming Substance: Gender in Material Sciences, Centre for Gender Research, Uppsala University, Sweden.
Lenin, V.I.: 1908/47, Materialism and Empiriocriticism; Critical Comments on a Reactionary Philosophy, trans. by A. Fineberg, Moscow: Foreign Languages Publishing House.
Longino, H.E.: 1990, Science as Social Knowledge: Values and Objectivity in Scientific Inquiry, Princeton: Princeton University Press.
Longino, H.E.: 1992, ‘Taking Gender Seriously in Philosophy of Science’, PSA, 1992 (2), 333-40.
Longino, H.E.: 1995, ‘Gender, Politics, and the Theoretical Virtues’, Synthese, 104, 383-97.
Longino, H.E.: 1997, ‘Feminist Epistemology as a Local Epistemology – I.’, Proceedings of the Aristotelian Society, Supplementary Volumes, 71, 19-35.
Longino, H. & Doell, R.: 1983, ‘Body, Bias, and Behavior: A Comparative Analysis of Reasoning in Two Areas of Biological Science’, Signs, 9, 206-27.
McMullin, E.: 1985, ‘Galilean Idealization’, Studies in History and Philosophy of Science, 16, 247-73.
Martin, E.: 1991: ‘The Egg and the Sperm: How Science Has Constructed a Romance Based on Stereotypical Male-Female Roles’, Signs, 16, 485-501.
Politis, V.: 2004, Aristotle and the Metaphysics, London & New York: Routledge.
Rodriguez-Pereyra, G.: 2011, ‘Nominalism in Metaphysics’, in: E.N. Zalta (ed.), The Stanford Encyclopedia of Philosophy (Fall 2011 Edition) [online at: http://plato.stanford.edu/archives/fall2011/entries/nominalism-metaphysics/].
Ross, D.: 2004, Aristotle, 6th ed., London & New York: Routledge.
Scheman, N.: 1996, ‘Though This Be Method, Yet There Is Madness in It: Paranoia and Liberal Epistemology’, in H.E. Longino & E.F. Keller (eds.), Feminism and Science, Oxford: Oxford University Press, pp. 203-19.
Spanier, B.B.: 1995, Im/partial Science: Gender Ideology in Molecular Biology, Bloomington & Indianapolis: Indiana University Press.
Spelman, E.V: 1982, ‘Woman as Body: Ancient and Contemporary Views’, Feminist Studies, 8, 109-31.
Spelman, E.V: 1988, Inessential Woman, Boston: Beacon Press.
Witt, C.: 2011, The Metaphysics of Gender, New York: Oxford University Press.
Ágnes Kovács:
Department of Gender Studies, Central European University, Nádor u. 9, 1051 Budapest, Hungary; kovacs_agnes@ceu-budapest.edu
Copyright © 2012 by HYLE and Ágnes Kovács
|