Why Mathematical Chemistry Cannot Copy Mathematical Physics and How to Avoid the Imminent Epistemological Pitfalls

  

Abstract: This paper argues that mathematical chemistry (MC) cannot just imitate mathematical physics (MP) but needs to develop its own interdisciplinary approach to avoid predictable obstacles. Although Kant’s dictum that chemistry does not lend itself to mathematical treatment was already refuted during his own lifetime, any useful combination of mathematics and chemistry essentially differs from MP. While the latter has a longstanding disciplinary tradition of its own, MC requires true interdisciplinary work and needs to bridge two fundamentally different methodological traditions. I suggest that MC follows methodological pluralism and develops new mathematical theories of chemistry that avoid telling causal stories. However, this makes MC susceptible to various epistemological pitfalls to be explained with examples from the earlier history of mathematical chemistry. I argue that all these pitfalls can be avoided through the collaboration with experimental chemists and finally point to geometrical symmetry theory as a model of a non-causal mathematical approach in science that emerged out of interdisciplinary efforts in 19^th-century mineralogy.

Keywords: mathematical chemistry, mathematical physics, methodology, epistemological pitfalls, causality, symmetry.

 

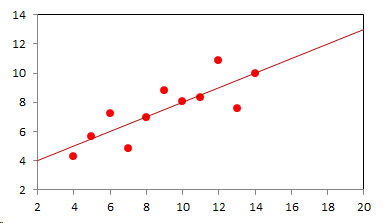
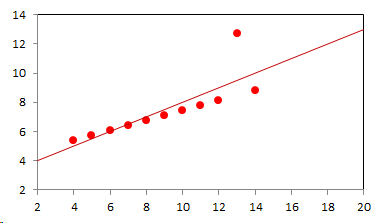
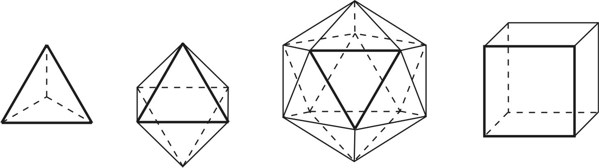
1. Introduction

At first glance mathematical chemistry and mathematical physics appear to be methodological twins: in each case there is a particular branch of a scientific discipline that uses mathematical methods to address its own issues. Yet while mathematical physics is centuries old and well established – even shapes the public image of physics more than anything else with prominent figures like Newton, Einstein, Dirac, and Feynman – mathematical chemistry only recently emerged as an own scientific subdiscipline, is still in its infancy and comparatively small.[2] This most obvious difference raises various questions: Does chemistry not lend itself to mathematical treatment as Kant once thought? Is there a particular affinity between mathematics and physics that helped establish mathematical physics quite early? Can mathematical chemistry simply take mathematical physics as a methodological model and copy its approach correspondingly in order to become equally successful?

In this paper I first argue that mathematical chemistry cannot just imitate mathematical physics but need to develop instead its own interdisciplinary approach (Section 2). Although Kant’s dictum that chemistry does not lend itself to mathematical treatment was already refuted during his own lifetime, as we will see, any useful combination of mathematics and chemistry essentially differs from mathematical physics. While the latter has a longstanding disciplinary tradition of its own that goes back to early ‘mixed mathematics’ and ‘rational mechanics’ before it was incorporated into modern physics, mathematical chemistry requires true interdisciplinary work between mathematics and chemistry. Moreover, because the methodology of chemistry, as the epitome of the experimental sciences, fundamentally differs from mathematical physics, as the epitome of the mathematically oriented sciences, mathematical chemistry needs to bridge two fundamentally different methodological traditions – which explains its comparatively late development. To cope with the methodological intuitions of chemists and to be distinguishable both from mathematical physics and physical chemistry, I suggest that mathematical chemistry follows the chemical model of methodological pluralism and develops new mathematical theories of chemistry that avoid telling causal stories.

However, abstinence from causality makes mathematical chemistry susceptible to various epistemological fallacies and pitfalls, which Section 3 explains with examples from the earlier history of mathematical chemistry: the pitfalls of empirical ignorance, aestheticism, numerology, incomprehensibility, number breeding, idealism, and blind statistical correlation. I finally argue that all these pitfalls can be avoided through interdisciplinary collaboration of mathematical chemists with experimental chemists and point to the most important historical model of a non-causal mathematical approach in science, the theory of geometrical symmetry that emerged out of interdisciplinary efforts in 19^th-century mineralogy.

2. The differences between chemistry and mathematical physics require a new approach for mathematical chemistry

2.1 Kant’s verdict: Is chemistry alien to mathematics?

In his Metaphysical Foundations of Science (1786), Immanuel Kant (1724-1804) wrote his notorious verdict about chemistry, that it "can be no more than a systematic art or experimental study, but never a proper science [eigentliche Wissenschaft]".[3] In order to assess this statement, it is important to consider that the German term "Wissenschaft" was still comparatively new at the time of his writing and that Kant was eager to define it according to his own rationalist ideal. In fact, for Kant proper science had to provide a priori knowledge, i.e. knowledge that is valid independent of any experience or experiments. Because he considered mathematics the only approach that provides a priori knowledge, he maintained that "the study of nature contains only as much proper science as mathematics can be applied in it". Living for almost all his life in Königsberg at the periphery of European science, he claimed in the heyday of the ‘Chemical Revolution’ that "chemical phenomena do not lend themselves to mathematical treatment", from which he concluded that chemistry was alien to science in his own peculiar sense. In Kant’s view, chemistry was not a proper science because mathematical chemistry would be impossible.

Curiously enough, Kant’s own student, Jeremias Benjamin Richter (1762-1807), would only a few years later disprove his professor with his PhD dissertation On the use of the mathematical method in chemistry (Richter 1789). It laid the groundwork for stoichiometry as an algebraic approach to chemistry, including what was later called the ‘law of constant proportion’ that John Dalton used for his atomism on chemical grounds (Richter 1792-3, Dalton 1808). Moreover, at the time of Kant’s writing, experimental philosophy was taking over most of the centers of European research to become the mainstream methodology of modern science, which would later denounce the ideal of a priori knowledge in science as ‘mere’ metaphysics. Although some philosophers of mathematical physics still adhere to that ideal today, Kant was a late partisan in the struggle for the methodological priority of mathematics in the study of nature as it was exemplified by the old field of ‘rational mechanics’. Yet, his view on science became marginalized as much as his verdict on chemistry, that it would be alien to mathematics, was refuted.

2.2 Different historical traditions of chemistry and mathematical physics

In the 17^th century, in some countries still in the 18^th century, the study of nature was largely divided into three main branches:[4] (1) natural history (historia naturalis) or the study of the animal, vegetable, and mineral kingdoms as well as geography, by more or less systematical observation; (2) natural philosophy (philosophia naturalis), also called physics (physica) in the original meaning, or the study of the causes and principles of natural bodies and phenomena, including, of course, the elements of matter and much of what we would today call chemistry; and (3) applied or mixed mathematics (mathematica mixta) or the measurement and the quantitative or geometrical description of natural phenomena, including astronomy, optics, and rational mechanics. Because natural philosophy traditionally had the highest status, both natural history and mixed mathematics frequently assumed to provide answers to philosophical questions, thereby blurring the division. Most successfully, mathematicians like René Descartes, Galileo Galilei, and Isaac Newton in the 17^th century managed to assume the status of natural philosophers by transforming the mathematical field of ‘rational mechanics’ into a new approach to natural philosophy, which Robert Boyle supported by calling it ‘mechanical philosophy’. Although still in the late 18^th century that was in many countries not considered to belong to physics in its original meaning but to mathematics,[5] the mechanical philosophy of nature should develop into today’s mathematical and theoretical physics.

It is important to note that mathematical physics did not result from some kind of interdisciplinary approach or merger by mathematics and physics, as the term might suggest to the modern reader. Instead, it had long been an integral part of applied mathematics, before it, due to the ‘purification’ of mathematics in the 19^th and 20^th centuries, moved into the science faculty to become later also called theoretical physics.[6] Thus, unlike typical interdisciplinary fields, mathematical or theoretical physics has not been built by combining different methodologies. Instead, it has always highlighted a priori reasoning as the path to scientific knowledge and required at most some empirical theory testing, which many 20^th-century philosophers of physics wanted to turn into a model for all the sciences.

That is entirely different in any possible meaning of ‘mathematical chemistry’. In fact, chemistry in the late 18^th century emerged as the epitome of experimental philosophy. Mary Jo Nye (1996, p. 9) cogently put it that, still in mid-19^th-century, "the word laboratory implied research in chemistry". In this tradition, experimentation has never meant testing mathematical theories. Instead it meant the exploration of new phenomena under new artificial conditions and the investigation of the causes of phenomena by the controlled manipulation of isolated material systems. As Thomas S. Kuhn (1976) once pointed out, the experimental or, as he called them, the ‘Baconian sciences’ continued to flourish in clear distance from the ‘mathematical tradition’ and vice versa well into the 20^th century. Whereas mathematical physics has always been the lead field of the ‘mathematical tradition’, any approach of mathematical chemistry needs to build a bridge between the two disconnected main traditions of science and their methodologies. That is the first important reason why mathematical physics cannot simply be a model for mathematical chemistry.

2.3 Methodological differences between chemistry and mathematical physics

There is a second, methodological reason that relates to the different status of theories in mathematical physics and the experimental sciences. When in the 17^th century mathematical approaches to nature were reformulated to aspire the status of natural philosophy, the epistemological level of their results upgraded from mere mathematical tools or the then so-called ‘hypotheses’ to ‘universal laws of nature’ or ‘worldviews’ (Bowler & Morus 2005, chap. 2). The most well-known example is the Copernican system in astronomy. In the 16^th century, the cleric Nicolas Copernicus had developed it largely as a calculational tool for the Christian needs of calendar reform, before aspiring mathematicians like Galileo in the 17^th century turned it into a new ‘worldview’ that would overthrow the received metaphysics. A second example, which is more relevant in the present context, is the reformulation of ancient corpuscularian metaphysics by Descartes, Newton, and others. By postulating mathematical ‘laws’ of locomotion (motus leges), the soon so-called ‘laws of nature’ for the speculative corpuscles and their interaction, which they supposed to be the material basis of Everything, they made strong metaphysical claims about the world that were hitherto unheard of by mathematicians.

The mathematical tradition that would eventually lead to mathematical and theoretical physics continued to follow the ideal of developing universal ‘laws’ of literally Everything. In its strongest version, ‘physicalism’, everything that does not obey its ‘laws’ is considered unreal or nonexistent. Yet, in its methodological version that matters here, the tradition of mathematical physics has always upheld the idea that there is ultimately only one true theoretical description of the world, which is, of course, a mathematical description. Thus, the guiding principle of theory development is unification, or at least reducing the number of different theoretical approaches by reducing them to a common basis. The underlying methodological principle of mathematical physics thus is methodological monism, such as the underlying metaphysical idea is that the world is ultimately simple, once the right mathematical approach has been found.

Contrast this view with the experimental sciences where any speculation can be called a theory and where the hard theoretical work consists in building reliable models. Rather than making a model ‘universal’, its reliability depends on defining clear-cut boundaries of application beyond which the model is useless. Indeed, in the experimental sciences, where the ideal of a theory of Everything is absent, pragmatic considerations of usefulness for certain kind of questions play an important role. Once context dependent relevance aspects are included in science, the ideal of methodological monism and its metaphysical twin of searching for a single true theory of Everything need to give way to methodological pluralism and pragmatism as well as the metaphysical idea that the world is ultimately complex (Schummer 2010). Chemistry (including physical chemistry, see Schummer 1998), the experimental science par excellence, has always developed a plurality of models, from different acid-base theories to the multitude of quantum-chemical models, which may overlap to some degree but which are each tailored to specific substance classes and questions of interest.

The fundamental methodological difference between chemistry and mathematical physics thus requires mathematical chemists to make a decision, provided they want to develop mathematical theories for chemistry. Once they follow the model of mathematical physics and take methodological monism as their ideal, their approaches might appear counter-intuitive to chemists. Moreover, if they integrate the causal structure of mathematical physics, the basic set of forces or interaction that physicists consider fundamental, mathematical chemistry might become indistinguishable from, or simply part of, mathematical physics. If on the other hand, they assume the causal structure of physics and the methodological pluralism of chemistry, it would be difficult to distinguish it from the long established physical chemistry. Indeed, because physical chemistry has always used mathematics, the mere usage of mathematics for chemical issues can hardly be characteristic of mathematical chemistry, unless one wishes to consider physical chemistry as part of the latter.

2.4 A methodological suggestion for defining mathematical chemistry

Thus, in addition to the criterion that mathematical chemistry develops mathematical theories for chemistry, we need further specifications to define its methodological identity in order to distinguish it from both mathematical physics and physical chemistry. I suggest that, like chemistry and physical chemistry, it follows methodological pluralism but refrains from causal theories or causal claims. After all, the strength of mathematics lies in its rigor and systematics to describe abstract structures. Chemistry heavily depends on structural concepts, both in the literal sense of molecular structure and the broader meaning of classificatory structures for substances and reactions or, more generally, entities and processes. Because the concepts of chemistry have frequently emerged historically rather than being systematically developed with mathematical rigor, there is plenty of work for mathematical chemistry. That expects to provide not only a clearer and more distinct language of chemistry, but also new frameworks of reasoning and systematics from which new insights can be derived.

While mathematical physics with its focus on causal change has historically developed along with (infinitesimal) calculus, recent mathematical chemistry employs and further develops other branches of mathematics, like topology (including knot theory and graph theory), cluster analysis, and group theory among others (e.g. King 2000, Trinajstić & Gutman 2002, Restrepo et al. 2004, Balaban 2005). None of these creative approaches claims to develop a universal theory of Everything, but they all point out important structures of chemistry from certain points of view. And all of these approaches focus on structural rather than causal features of chemistry, such that they comply with the definition given above.

Developing new mathematical approaches to chemistry is not without methodological difficulties, however, particularly if a causal nexus is ignored that would considerably restrict the kind of reasoning. Indeed there are various pitfalls that mathematical chemists should avoid. To illustrate that, the following section provides a brief outline of these pitfalls along with examples from the almost forgotten earlier history of mathematical chemistry, before I show how to avoid these pitfalls and then briefly mention geometrical symmetry as a model for mathematical chemistry.

3. Imminent pitfalls of mathematical chemistry and how to avoid them

3.1 The pitfall of empirical ignorance

Whereas mathematical chemistry is for many a recent development, it is arguably one of the oldest theoretical approaches to what we would call chemistry. Indeed, Plato’s mathematical theory of elemental change from the 4^th century BC, outlined in his dialogue Timaios (53c-56c), has rightly been called the oldest molecular theory which is still discussed today (Rex 1989, Visintainer 1998, Lloyd 2007). In this theory, the so-called platonic solids (tetrahedron, octahedron, icosahedron, and cube) represent the four elements (fire, air, water, and earth) (see Figure 1). The first three solids are composed of right-angled triangles with different legs, and thus can, at least theoretically, be transformed into each other, for instance, when water and fire turn into air (vaporization). However, the earthy cube consists only of isosceles triangles which cannot build up any of the other solids but only different kinds of cubes. Plato’s theory therefore forbids the transformation of earths (e.g. stones, metals, and salts) into liquids or gases. While such transformations are indeed comparably rare in daily life, they were already well-known to Plato’s contemporaries who used, for instance, the melting of metals and the solution of salts in the crafts of metallurgy and tannery, respectively.[7]

The ignorance of empirical facts is likely to be the major problem in any theoretical science. Mathematical chemists, who of course cannot know any of the myriads of chemical facts, could try to avoid the pitfall by working closely together with experimental chemists.

(a)

(b)                          (c)

Figure 1. (a) The platonic solids (tetrahedron, octahedron, icosahedron, and cube) representing the four elements fire, air, water, and earth. The first three are composed of right-angled triangles with different legs (b) whereas the cube consists of isosceles triangles (c).

3.2 The pitfall of aestheticism

There are various reasons why one can be tempted to ignore empirical facts. One is aestheticism that favors simple, elegant theoretical formulations per se. Plato’s choice of the regular polyhedrons and the two kinds of triangles was explicitly guided by the idea that nature is inherently beautiful (Timaios, 53e-54a). It is likely that such aesthetic assumptions have always played a role whenever the platonic solids appeared in the history of science, including chemistry (Schummer 2009). Although Alfred Werner (1866-1919) developed his famous theory of coordination polyhedra in inorganic chemistry on the basis of painstaking arguments resting on numerous experiments and symmetry consideration (Werner 1913), he and his followers were probably not entirely free of aesthetic ideals. Still today coordination polyhedra are presented in inorganic chemistry textbooks as epitomes of the beautiful symmetry of nature. Yet, as Hermann Arthur Jahn (1907-79) and Edward Teller (1908-2003) showed already in 1937, under certain conditions the distortion of coordination polyhedra is energetically favored. The general lesson from the Jahn-Teller effect is that ‘nature’ frequently ‘prefers’ distortion over symmetry and purist beauty, a lesson that in some regard also follows from the entropy principle in thermodynamics.

In the experimental sciences like chemistry, mathematical simplicity is usually justified only as a first-order approximation rather than on the putative grounds of the inherent beauty or simplicity of nature. Mathematical chemists who disregard that may easily fall victim to the pitfall of aestheticism.

3.3 The pitfall of numerology

Scientists have frequently expressed a clear liking for specific numbers or patterns, which is either a derivation of aestheticism or an expression of mysticism. Examples from the history of alchemy and chemistry abound. The most notorious one is the dogma of seven, according to which there would be only seven metals in correspondence to the dogma of the seven celestial bodies and the seven days of divine Creation. Contrary to modern hagiography of science, a scientist like Johannes Kepler (1571-1630) spent much of his early efforts at geometrically proving the ‘holiness’ of the number seven – corresponding to the five Platonic bodies that, when nested into each other in a certain order, could be inscribed and circumscribed by the spherical orbits of the six planets, plus the sun as the seventh body – as well as that of the number three according to Christian trinity (Kepler 1596). Numerology not only made people blind in astronomy, where one could have easily transcend the number seven (six planets plus sun, but excluding the moon), but even more so in alchemy which for many centuries stuck to the idea that there are exactly seven corresponding metals (sun=gold, moon=silver, mercury=quicksilver, venus=copper, mars=iron, jupiter=tin, saturn=lead, excluding the earth). However, beyond these classical astrological seven metals, many metals had been known since antiquity like antinomy, arsenic, zinc, bronze, brass, and others that did not fit the scheme. If you think that such liking is part of the far past only, consider for instance the ‘knight’s move’ and other patterns that have been projected on the periodic system of chemical elements (Rourvray & King 2004).

When experimental results do not provide any guidance, numerology like aestheticism regularly appears in theoretical science. Mathematical chemists should be informed about the cultural history of such arguments in order to evaluate them from a scientific point of view, rather than waiting for or taking advantage of a Hitchhiker’s Guide to the Galaxy.[8]

3.4 The pitfall of incomprehensibility

Mathematics not only has its own language, it also cultivates its own standards for developing new language – of rigor in definitions and of abstractness that makes it suitable for many cases. Whoever explores a new field from a mathematical point of view, must develop a new language that people already working in the field are not familiar with. The obvious danger is being incomprehensible or misunderstood by those who used to work in the area. Indeed the history of mathematical chemistry is full of idiosyncratic scholars who, because regular chemists found them largely incomprehensible, are often forgotten. A little more well-known examples are the British chemist Benjamin Collins Brodie (1817-1880), who developed an algebraic approach to chemical operations, and the Bohemian chemist František Wald (1861-1930), who tried to derive the stoichiometric laws a priori (Brock 2002, Ruthenberg 2007). The important works on chemical thermodynamics by the American scientist Josiah Willard Gibbs (1839-71), who eventually became one of the founding fathers of that field, would probably have remained unknown to European chemists (and American chemists and physicists alike, according to Servos 1990, p. 356), if the then leading physical chemist Wilhelm Ostwald (1853-1932) had not promoted his work through translational and explanatory efforts (Gibbs 1892).[9]

Because it would be naive to assume that there is always a translator like Ostwald around, mathematical chemists should take particular care of remaining comprehensible by ordinary chemists, of sensibly choosing their vocabulary and of writing different versions of their work for different audiences.

3.5 The pitfall of number breeding

At the 1959 Boulder Conference, Charles A. Coulson (1910-1974) envisioned a new generation of computational chemists who would discard all chemical concepts (including quantum chemical models) in favor of calculating only accurate numbers, particularly energy values (Coulson 1960). This is not the place to assess the historical development of quantum chemistry since then. Moreover, it is understood that accurate measurements, or calculated numbers for that matter, are frequently important in chemistry. However, it should be clear that most questions in science, in particular all why-questions, cannot sufficiently and meaningfully be answered through numbers only. Chemistry usually seeks explanations that numbers alone can hardly provide. Consider, for instance, the question: ‘Why does compound A react with compound B?’ A pure computational chemist can only respond: ‘Because the reaction product has a lower energy than A and B according to my calculation.’ The problem with the answer is that it was already known before the calculation even started. Indeed the basic laws of chemical thermodynamics, the axioms if you want, require that reaction products always have a lower energy (free enthalpy) than the starting materials.

The example illustrates that mathematical chemists, provided they produce quantitative results, need to look carefully at what questions matter in chemistry and what a meaningful answer is in each case. Sometimes numerical accurateness is important; sometimes it does not matter at all.

3.6 The pitfall of idealism

Every now and then it becomes fashionable to use the term ‘experiment’ for something entirely different from what experiments proper are in science. For instance, when experimental philosophy began to dominate natural philosophy in the early 19^th century, German idealists were quick to usurp the term to denote all kinds of reasoning in metaphysics, theology, and even speculative politics as ‘experimental’.[10] Recently, philosophers of mathematical physics have rediscovered the scholastic concept of ‘thought experiments’ and, more recently, are engaged in the methodology of ‘computer experiments’ (e.g., Sorensen 1992, Brown 1993, Humphreys 2004, Winsberg 2010). However, neither speculative thinking nor algorithmic calculations can perform anything equivalent to scientific experimentation. Proper experiments, as the term is used in the experimental sciences (and anywhere else outside of the philosophy of mathematical physics), are based on the realist assumption that their outcome is neither controlled nor totally predictable by human reasoning, that they instead probe material reality independent of human intellect. If one instead confuses or, as idealism does, intentionally gives up the distinction between the real world, on the one hand, and our views, models, theories, or computer simulations of the world, on the other, there is no need for experiments any more.

Because the expression suggests that ‘computer experiments’ would be a surrogate for experiments, computational chemists, like theoretical scientists in general, are prone to develop their own computer simulation world that loses contact to the real world, including the world of experimental chemists.

3.7 The pitfall of blind statistical correlation

Finally, applied mathematicians sometimes tend to overlook important mathematical insights, among which the warning of over-interpretations of statistical correlations features most prominently. In current mathematical chemistry, the interpretation of correlations actually plays an important role when for instance a molecular structure index is correlated with a biochemical or pharmacological property. It is usually clear in science that correlations do not tell you anything about cause-effect relationships – despite a misleading Humean tradition, which is still alive in the received philosophy of science that tend to confuse both. More important in this context, most standard statistical values can be indistinguishable for a broad variety of different data sets. For instance, a strong Pearson correlation of, say, 0.8 with a strong 95% confidence can result from many different relationships between x and y values (Figure 2), from which no conclusion about functional dependencies can be drawn (Anscombe 1973). 

Figure 2: Four examples of different distributions of each 11 data pairs that show exactly the same standard statistical values, such as the same mean values for x and y (9.0 and 7.5), the same linear regression line with the same regression coefficient (y = 3 +0.5x), the same standard error of 1.237, and the same strong Pearson correlation of 0.816 at the same confidence level of 0.95 (after Anscombe 1973).

Mathematical chemists should not only beware of the pitfalls of statistical correlation, and always consult the graphical representations before drawing any conclusions from statistical values alone, they should also be particularly careful in communicating correlation results to others who tend to misinterpret these results as relations of either cause-effect or proportionality.

3.8 Avoiding the pitfalls

All the mentioned pitfalls arise from taking one’s own mathematical approach too seriously at the expense of other views and aspects on the same matter. This is immediately clear for the pitfall of empirical ignorance and its derivatives of aestheticism and numerology, as they ignore empirical input by celebrating certain ideals – theoretical, aesthetic, or mystic. The pitfalls of incomprehensibility and number breeding result from a lack of communication with experimental chemists, which usually helps keep to a comprehensible language and stay in touch with the kind of questions that actually matter in chemistry. Idealism that confuses its own computer simulations with chemical experiments is rather on the extreme side as it seems insusceptible to external views, whereas the pitfalls of statistical correlation could at least be corrected by mathematical means alone – or by simple visualization of the data.

Although all of these pitfalls can play a role in any mathematical or theoretical science, they are particularly important when further theoretical guidance in addition to mathematical standards is missing. Most importantly, they can easily arise when a causal theory of cause-effect relationship is missing or irrelevant. If mathematical chemistry, as suggested above, avoids cause-effect relationship or forces, it is particularly prone to these pitfalls.

The easiest remedy, rather than assuming cause-effect relationships from physics to become indistinguishable from physics or physical chemistry (see above), is collaborating with experimental chemists. In other words, the more mathematical chemistry avoids causal stories in favor of describing the mathematical structure of chemistry, the more it should be performed in collaboration, or at least in strict accordance, with experimental chemistry. Whereas philosophers of (mathematical) physics might suggest a division of labor between the invention of theories by heroic mathematical physicists and the legwork of testing those theories by experimental physicists, the philosophy of chemistry point of view that I defend here is entirely different: Mathematical chemists should work from the very beginning in close collaboration with experimental chemists on the development of research questions, chemical concepts, and models. After all in contemporary science teamwork has been the rule for long, unlike the socially isolated researcher that still dominates the public and, unfortunately, also the philosophical image of science.

3.9 The model of mathematical symmetry

The previous subsections, while highlighting pitfalls and fallacies, might lead to the wrong impression that mathematical chemistry is rather a problem than a useful contribution to chemistry. However, such a view would underestimate the extraordinary potential of mathematics in chemistry. Although, correctly speaking, it historically did not arise from chemistry but from its then closely related field of mineralogy, the mathematical theory of symmetry is perhaps the best historical model of how mathematics and chemistry could fruitfully interact.

Unfortunately the history of the concept of symmetry has been covered by decades and layers of misleading popularizations of science.[11] It was probably Hermann Weyl in his book Symmetry (1952) who first coined the myth, according to which mathematical symmetry had been already invented by the ancient Greeks, even though in a preliminary state, and then waited to be rediscovered and generalized by modern mathematics and mathematical physics.[12] Most later popularizers fell victim of the term ‘symmetry’ or Greek ‘symmetría’ that literarily meant ‘with appropriate measure’ and which was used in ancient Greek art theory to describe aesthetically perfect proportions, like the proportion between the head and the body, but also a well-balanced depiction combining opposite aspects such as statics and dynamics (Schummer 2006). Although the Pythagoreans and Platonists aesthetically favored the platonic solids and other forms for their regularity of lengths and angles or geometrical symplicity, they never expressed the modern idea of mathematical symmetry, in the sense of being invariant to a certain set of geometrical transformations.

Instead, modern symmetry was developed only in 19^th-century mineralogy by a fruitful interaction between mathematics and natural history, to which mineralogy as a classificatory approach then belonged.[13] Indeed it emerged out of the classification of minerals by crystal shape and structure. Roughly speaking it resulted from interactions between the French structural atomistic school and the German dynamistic school, by combining natural history, natural philosophy, and mathematical traditions. In France, René-Just Haüy (1743-1822) had laid in 1801 the groundwork for a geometrical classification of crystals by distinguishing between five basic forms of crystals, which Bravais later in 1849 through an atomistic interpretation elaborated into his system of 14 basic lattices. On the German side, where dynamism prevailed early 19^th-century natural philosophy, Christian Samuel Weiss (1780-1856) developed in 1815 seven crystal systems from dynamic force axes, which he considered responsible for crystal growth and which later came to be known as symmetry axes. His approach was further developed by Johann F. C. Hessel (1796–1872) who around 1830 derived 32 crystal classes from symmetry operations in the modern sense, which correspond to today’s 32 point groups. Eventually in 1889/91 two mathematicians, Arthur Moritz Schoenflies (1853-1928) and Yevgraf S. Fyodorov (1853-1919), arrived at the system of 230 possible crystal lattices by applying the then generalized group theory to crystallography. Although geometrical symmetry was eventually integrated into the independently developed algebraic group theory, it originally emerged out of the need to classify minerals by mathematical means and philosophical inspiration.

Nowadays mathematical symmetry is such a general theory to describe any objects in space that its mineralogical origin is not only invisible but also largely forgotten. And yet it is an outstanding model from the history of science of how mathematics can help develop a classification system that covers all possible cases and distinguishes them both precisely and in a relevant manner. Lacking any roots in mathematical physics, it is a model of structural, non-causal mathematical theories in science. Once developed, it became an extremely useful tool in many areas, including chemistry where it was soon used to predict (and produce) new crystals. Moreover, mathematical symmetry theory became indispensable in classical molecular structure elucidation by predicting the number of possible isomers that result from particular chemical modifications, and last but not least in molecular spectroscopy and quantum chemistry.

4. Conclusion

Less than fifty years ago, philosophy of science was almost totally confined to philosophy of mathematical physics. Moreover, the philosophers of those days were so enthusiastic about this discipline, in which they had frequently obtained their first degree, that they recommended its methodology as the ideal of any science. Apart from some newly emerging social sciences, their recommendations had little to no recognizable impact on other disciplines, however. Although philosophy of science nowadays still keeps that disciplinary focus to a considerable degree, it has slowly become aware of the rich diversity of scientific methods and traditions, among which mathematical physics is unique in many regards and hardly comparable or transferable to other disciplines, like chemistry, biology, and even experimental physics. The methodological similarity appears more plausible with regard to corresponding subdisciplines like mathematical chemistry or mathematical biology.

In this paper I have argued that the prima facie plausibility is misleading even with regard to mathematical chemistry. While mathematical physics is in many regards a discipline of its own that emerged from applied or mixed mathematics, mathematical chemistry is required to build a true interdisciplinary bridge between mathematics and chemistry. The difference explains the late disciplinary emergence of mathematical chemistry, while ignorance of the difference might be responsible of former unfortunate efforts to establish the field. Mathematical chemists should be aware that they cannot take mathematical physics as a model; they have to go their own way instead. Methodological reflection is indispensable on that road because various dangers are looming. One is being counter-intuitive to ordinary chemists, which would render it irrelevant. Another is being indistinguishable from mathematical physics or physical chemistry, which would deprive mathematical chemistry of its identity and thus make it irrelevant too. Finally, even if one follows the methodological suggestions I gave here for being both intuitively clear to chemists and distinguishable – following methodological pluralism and providing structural rather than causal theories – there are many epistemological pitfalls and difficulties that mathematical chemists should be aware of in order to avoid them. All these dangers require proactive reflections to define the methodological identity of mathematical chemistry

Apart from pure methodological reflection, the history of mathematical approaches to chemistry offers surprisingly rich lessons to learn from, both negative and positive cases mentioned in Section 3, that each would require more in-depth analysis. Which illustrates that the history and philosophy of science, rightly understood, is an important component to any new and creative development of science such as mathematical chemistry.

Acknowledgments

I am grateful to one of the two anonymous referees and to Guillermo Restrepo for useful comments on an earlier version.

Notes

[1]  This paper was first presented at the Second Mathematical Chemistry Workshop of the Americas, Universidad de los Andes, Bogota, Colombia, 19-24 July 2010.

[2]  It is important here to distinguish between mere concepts and scientific approaches (cognitive body) and a scientific discipline in the proper meaning of a social body organized around a cognitive body. Although the application of mathematics to chemistry has a much longer tradition, even apart from what has been called physical chemistry since the late 19th century (see Section 3), the discipline of mathematical chemistry emerged only a few decades ago with an own scholarly society, journals, professorships, etc. (see Restrepo & Villaveces 2012, in this volume). For a methodological defintion of mathematical chemistry, see Section 2.4.

[3]  All translations are mine from the German original (Kant 1786, p. AXf.). On Kant’s view of chemistry, see particularly van Brakel 2000, pp. 7-13 and Vasconi 1999.

[4]  In England some changes occurred already in the 17^th century, see e.g. Garber 2010; in the German speaking countries, the most comprehensive Encyclopedia of the 18^th century (Zedler 1723 ff.) clearly distinguished between physics and mathematics in its article on ‘Naturlehre’ (vol. 23, cc.1147-67) and dealt separately with ‘Naturgeschichte’ (vol. 23, cc. 1063-85); for late 18th-century France, see the note below.

[5]  For instance, in the French Academy of Science, mechanics and astronomy belonged to the mathematical division still in 1785 whereas the ‘physical sciences’ included chemistry, metallurgy, mineralogy, botany, agriculture, natural history, and anatomy (Kuhn 1976, p. 19).

[6]  For the disciplinary development of modern physics, see particularly Stichweh 1984. Note that in England theoretical physics belonged to mathematics still for most of the 20^th century, as is illustrated by the careers of scholars like Paul Dirac and Charles Coulson who were both chairs of mathematics in Cambridge and Oxford, respectively.

[7]  The only way to avoid the empirical inconsistency is to consider metals as largely composed of water, as most of the alchemists did, and the solution of salts as a kind of microdispersion too small for the naked eye. But that runs into other problems that cannot be discussed here.

[8]  See Adams 1982, where a supercomputer calculates the number 42 as the answer to "the ultimate question of life, the universe, and everything".

[9]  The delayed reception of Gibbs’ work on chemical thermodynamics by chemists stands in contrast to the comparatively soon recognition of his mathematical contributions, particularly his vector analysis, by physicists, which further illustrates the different attitude to mathematics by chemists and physicists.

[10]  For instance, Novalis considered the history of philosophy a history of ‘experimental attemps’, Schlegel called the method of his idealism ‘combinatorical experimentation’, it became fashionable to talk of ‘experimental religious studies’ (Novalis), ‘experimental politics’ (Lichtenberg) and ‘experimental metaphysics’ (Schopenhauer) (See Kuhlen & Schneider 1972).

[11]  On the following see Schummer 2006.

[12]  To be fair, Weyl (1952, S. 6) at first acknowledged the different concepts, but only to blur the difference afterwards with an obscure argument: He started with dividing the ancient symmetry concept in art into the general idea of balanced proportions and a "particular" concept of bilateral symmetry. Then he correctly refomulated the latter concept in modern mathematical terms to show that it is a special case of general mathematical symmetry. Finally, he wrongly presented general mathematical symmetry as a "precision" of the "unclear" general concept of symmetry in art that would have been guided "by the mirages of philosophy".

[13]  For the historical origin of mathematical symmetry in mineralogy, see Scholz 1989.

References

Adams, D.: 1982, Life, the Universe, and Everything, Pan Books, London (no. 3 of the series Hitchhiker’s Guide to the Galaxy).

Anscombe, F.J.: 1973, ‘Graphs in statistical analysis’, The American Statistician, 27, 17-21.

Balaban, A.T.: 2005, ‘Reflections about Mathematical Chemistry’, Foundations of Chemistry, 7, 289-306.

Bowler, P.J. & Morus, I.R.: 2005, Making Modern Science: A Historical Survey, University of Chicago Press, Chicago & London.

Brock, W.: 2002, ‘Sir Benjamin Collins Brodie (1817-1880)’, Hyle: International Journal for Philosophy of Chemistry, 8, 49-54.

Brown, J.R.: 1993, The Laboratory of the Mind: Thought Experiments in the Natural Sciences, Routledge, London.

Coulson, C.A.: 1960, ‘Present State of Molecular Structure Calculations’, Reviews in Modern Physics, 32, 169-177.

Dalton, J.: 1808, A New System of Chemical Philosophy, Bickerstaff et al., Manchester.

Garber, D.: 2010, ‘Philosophia, Historia, Mathematica: Shifting sands in the disciplinary geography of the seventeenth century’, in: Tom Sorell et al. (eds.): Scientia in early modern philosophy, Springer, Dordrecht, pp. 1-18.

Gibbs, J.W.: 1892, Thermodynamische Studien, trans. and ed. by W. Ostwald, Engelmann, Leibzig.

Humphreys, P.: 2004, Extending Ourselves: Computational Science, Empiricism, and Scientific Method, Oxford University Press, Oxford.

Jahn, H.A. & Teller, E.: 1937, ‘Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy’, Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, 161, 220-35.

Kant, I.: 1786, Metaphysische Anfangsgründe der Naturwissenschaft, Hartknoch, Riga.

Kepler, J.: 1596, Mysterium Cosmographicum, Gruppenbachius, Tübingen.

King, R.B.: 2000, ‘The Role of Mathematics in the Experimental/Theoretical/Computational Trichotomy of Chemistry’, Foundations of Chemistry, 2, 221-36.

Kuhlen, R. & Schneider, U.: 1972, ‘Experimentalphilosophie’, in: J. Ritter et al. (eds.), Historisches Wörterbuch der Philosophie, vol. 2, Schwabe, Basel.

Kuhn, T.S.: 1976, ‘Mathematical vs. Experimental Traditions in the Development of Physical Science’, Journal of Interdisciplinary History, 7, 1-31

Lloyd, D.R.: 2007, ‘The Chemistry of Platonic Triangles: Problems in the Interpretation of the Timaeus’, Hyle: International Journal for Philosophy of Chemistry, 13, 99-118.

Nye, M.J.: 1996, Before Big Science: The Pursuit of Modern Chemistry and Physics, 1800-1940, Twayne, New York & London (reprinted 1999 by Harvard University Press).

Restrepo, G.; Mesa, H.; Llanos, E. J.; Villaveces, J. L.: 2004, ‘Topological study of the periodic system’, Journal of Chemical Information and Computer Sciences, 44, 68-75.

Restrepo, G. & Villaveces, J. L.: 2012, ‘Discrete mathematical chemistry, a social perspective of its emergence and reception’, Hyle: International Journal for Philosophy of Chemistry, 18, forthcoming.

Rex, F.: 1989, ‘Die Älteste Molekülartheorie’, Chemie in unserer Zeit, 23, 200-6.

Richter, B.R.: 1789, De usu matheseos in chymia (On the use of the mathematical method in chemistry), PhD dissertation, University of Königsberg.

Richter, B.R.: 1792-3, Anfangsgründe der Stöchyometrie oder Meßkunst chymischer Elemente, 3 vols., Korn, Breßlau & Hirschberg.

Rourvray, D.R. & King, R.B. (eds.): 2004, The Periodic Table: Into the 21^st Century, Institute of Physics, Baldock.

Ruthenberg, K.: 2007, ‘František Wald (1861-1930)’, Hyle: International Journal for Philosophy of Chemistry, 13 (1), 55-61.

Scholz, E.: 1989, Symmetrie, Gruppe, Dualität: Zur Beziehung zwischen theoretischer Mathematik und Anwendung in Kristallographie und Baustatik des 19. Jahrhunderts, Birkhäuser, Basel et al.

Schummer, J.: 1998, ‘Physical Chemistry: Neither Fish nor Fowl?’, in: P. Janich & N. Psarros (eds.): The Autonomy of Chemistry, Königshausen & Neumann, Würzburg, pp. 135-48.

Schummer, J.: 2006, ‘Symmetrie und Schönheit in Kunst und Wissenschaft’, in: W. Krohn (ed.), Ästhetik in der Wissenschaft, Meiner, Hamburg, pp. 59-78.

Schummer, J. : 2009, ‘Aesthetic Values in Technology and Engineering Design: Designing Small-scale objects: chemistry’, in: A. Meijers (ed.), Philosophy of Technology and Engineering Sciences, Elsevier, Amsterdam et al., p. 1044-54.

Schummer, J.: 2010, ‘Philosophy of Chemistry’, in: F. Allhoff (ed.), Philosophies of the Sciences: A Guide, Wiley-Blackwell, Chichester, pp. 163-83.

Servos, J.W.: 1990, Physical Chemistry from Ostwald to Pauling: The Making of a Science in America, Princeton University Press, Princeton.

Sorensen, R.A.: 1992, Thought Experiments, Oxford University Press, Oxford.

Stichweh, R.: 1984, Zur Entstehung des modernen Systems wissenschaftlicher Disziplinen: Physik in Deutschland, 1740-1890, Suhrkamp, Frankfurt.

Vasconi, P.: 1999, Sistema delle scienze naturali e unità della conoscenza nell’ultimo Kant, Olschki, Firenze.

van Brakel, J.: 2000, Philosophy of Chemistry: Between the Manifest and the Scientific Image, Leuven University Press, Leuven.

Visintainer, J.: 1998, ‘A Potential Infinity of Triangle Types: On the Chemistry of Plato’s Timaeus’, Hyle: International Journal for Philosophy of Chemistry, 4, 117-28.

Werner, A.: 1913/1966, ‘On the Constitution and Configuration of Higher-Order Compounds’, in: Nobel Lectures, Chemistry 1901-1921, Elsevier, Amsterdam, pp. 256-69.

Weyl, H.: 1952, Symmetry, Princeton University Press, Princeton.

Winsberg, E.: 2010, Science in the Age of Computer Simulation, Chicago University Press, Chicago.

Zedler, J.H. (ed.): 1723-54, Großes vollständiges Universal-Lexikon, 68 vols., Zedler, Halle & Leipzig.

Joachim Schummer:
Berlin, Germany; js@hyle.org