Mathematical Thinking in Chemistry

  

Abstract: Mathematical chemistry is often thought to be a 20^th-century subdiscipline of chemistry, but in this paper we discuss several early chemical ideas and some landmarks of chemistry as instances of the mathematical way of thinking; many of them before 1900. By the mathematical way of thinking, we follow Weyl’s description of it in terms of functional thinking, i.e. setting up variables, symbolizing them, and seeking for functions relating them. The cases we discuss are Plato’s triangles, Geoffroy’s affinity table, Lavoisier’s classification of substances and their relationships, Mendeleev’s periodic table, Cayley’s enumeration of alkanes, Sylvester’s association of algebra and chemistry, and Wiener’s relationship between molecular structure and boiling points. These examples show that mathematical chemistry has much more than a century of history.

Keywords: mathematical chemistry, mathematical way of thinking, functional thinking, chemical graphs, QSAR.

 

1. Introduction

Mathematical chemistry, or better, discrete mathematical chemistry (Restrepo & Villaveces 2012), appeared as a new subdiscipline in the second half of the 20^th century. Instances of it are the launching of three scientific journals devoted to mathematical chemistry,[1] the creation of the International Academy of Mathematical Chemistry,[2] the publication of specialized books on mathematical chemistry, and the scientific meetings on the subject that currently gather a growing scientific community. The fact of having consolidated a community in the second half of the 20^th century suggests that the relationship between mathematics and chemistry is something new, perhaps beginning in the 20^th century. The purpose of this paper is to show that, besides the contemporary mathematical chemistry consolidation, there are instances of close contact between mathematical and chemical thinking dating back centuries ago. We discuss several examples to support our statement.

2. Mathematical way of thinking

Hermann Weyl, in 1940, published a paper entitled ‘The mathematical way of thinking’. There, the influential German mathematician and physicist, following Felix Klein’s ideas settled in the Erlangen Program of 1872, claimed that mathematical thinking has to follow functional thinking, i.e. "thinking in terms of variables and functions" (Weyl 1940), which consists of three steps:

1. Make clear the kind of variables to ponder on.
2. Represent variables by symbols.
3. Build up functions mapping one variable upon the other.

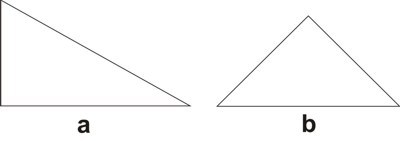
By ‘variable’ it is meant a quantity whose value may vary;[3] ‘symbol’ is understood as the labeling of the variable;[4] by ‘function’ it is meant the process of assigning to each element of a first set a unique element of a second set, the first and the second set can be the same.[5]

It is important to state that a function is different from a relation, which assigns elements of a first set to elements of a second set (that may be the same set), but does not require that for each element of the first set a unique element exists in the second set, which is what a function does. Hence, a function is a particular kind of relation, but any relation is not necessarily a function.

As an example of functional thinking, let us take the case of kinematics, where one has to deal with mobile objects that are studied on the basis of the time of the movement and the space through which the objects travels. Therefore, a suitable set of variables is made by space and time, which are further labeled as s and t, respectively. A function relating those variables is t  →  s, or better s = ½ gt², where for each value of time a value of the space variable is given.

The first step of Weyl’s mathematical way of thinking is important because it gives, from the plethora of options, the relevant things to study for developing new knowledge. The second step, the labeling by using symbols, seems at first glance not important. However, as Weyl warns, "words are dangerous tools" (Weyl 1940), for they lead the mind to the manifold connotations words carry with them, which may constitute an obstacle for reaching the next step.[6] The third step is where the abstraction attained by symbolizing gains generalization and the variables become related to each other.

The kind of thinking framed in the previous three steps, not necessarily leading to mathematical conclusions, is what Weyl calls the mathematical way of thinking. One could think that simple counting is a form of mathematical thinking, because there is a function between the set of objects to be counted and the set of natural numbers. Although it is true that such a function exists, the customary use of those functions makes the process a routine. However, according Weyl, the mathematical way of thinking is not "reducible to a set of mechanically applicable rules" (Weyl 1940). The first humans associating objects with natural numbers actually practiced a mathematical way of thinking. We, the mere ‘users’ of that way of thinking when we simply count, are not aware of the innovative effort of our ancestors, the result of which has been given to us through education.

Before continuing, it is worth discussing the relationship between functional thinking and relational thinking. Examples of relational thinking include the drawing of analogies between seemingly different objects or events, applying abstract rules in novel situations, and understanding and learning a language (Doumas & Hummel 2005, p. 73). According to Doumas & Hummel (ibid.) "relational thinking" underlies "everything from the mundane to the sublime (e.g., Cantor’s use of set theory to prove that the cardinal number of the reals is greater than the cardinal number of the integers)". Hence, as function is contained in the concept of relation, functional thinking is contained in relational thinking.

At this stage on can think that Weyl’s approach to the mathematical way of thinking implies that any kind of rational thinking is mathematical. For example, reading this text makes the reader go from the set of words, symbolized by the finite set of letters in these pages, to the set of meanings. Although this example may indeed be a mathematical way of thinking, there are different degrees. If knowledge is built by defining a clear set of objects and a clear set of functions relating elements of both sets to another, then this is a way of mathematical thinking at a high degree. An example is Cantor’s proof using set theory above mentioned. In contrast, if the knowledge construction defines loosely or not at all the sets and does not care about definitions of the relations between elements of different sets, then its mathematical way of thinking is of lower degree. An example of this situation is the act of catching a bus, where the set of possible destinations is important, as well as the set of persons that are already in the bus and the set of coins one has in the pocket. Here the function goes from the mentioned sets to the set of decisions: catching or not the bus. Thus, the mathematical way of approaching knowledge is a question of degrees.

In this paper we show that there are many examples of chemical knowledge acquired by the application of the three steps of mathematical thinking. We consider these examples instances of a high degree of mathematical thinking.

2.1 Plato’s triangles

In his dialogue Timaeus (53c-56c), Plato (c. 424-348 BC) developed a theory of nature, its constitution and change based upon the earlier four elements of Greek philosophy (water, air, earth, and fire). He associated to each element a regular polyhedron: tetrahedron (fire), octahedron (air), hexahedron (earth), and icosahedron (water), leaving the dodecahedron for the entire Cosmos. All five polyhedra were constructed by using Plato’s truly elementary units: stoicheia,[7] i.e. two particular right triangles (Figure 1) (Lloyd 2007).

Figure 1: Stoicheia: (a) scalene triangle with angles of 30º, 60º, and 90º; and (b) isosceles triangle with angles of 45º, 90º, 45º.

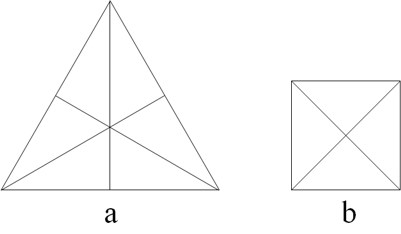
Different sizes of polyhedra yielded different macroscopic properties, e.g., different tetrahedron sizes are associated to conventional fire and light of different colors.[8] Plato went beyond by looking for similarities among his elements. He found that four regular polyhedra may be formed by assembling equilateral triangles (four for a tetrahedron, eight for an octahedron, etc.). These triangles, in turn, are made up by assembling six stoicheia, i.e. scalene triangles with angles of 30º, 60º, and 90º (Figure 2a) (Lloyd 2007). Hence, elements made from polyhedra resulting by assembling the same kind of stoicheia can convert into each other, i.e. water into air, air into fire, etc. As the squares in the cube (hexahedron) are made up of right-angled isosceles triangles (Figure 2b) that cannot be obtained by assembling the scalene triangles discussed before, Plato concluded that earth (cube) cannot convert into fire (tetrahedron), air (octahedron), and water (icosahedron).

Figure 2: Assembling of (a) six stoicheia (scalene triangles with angles of 30º, 60º, and 90º) to form an equilateral triangle suitable for constructing tetrahedra, octahedra, dodecahedra and icosahedra; (b) four stoicheia (isosceles triangles with angles of 45º, 90º, and 45º) to form a square only suitable for constructing hexahedra (cubes).

Plato used mathematics to refer to his chemical ideas, and, as pointed out by Lloyd (2007), he used the most advanced mathematics of his time, geometry.

Plato’s ideas may be framed in the mathematical way of thinking as follows:

1. Variables: stoicheia, fire, air, earth, and water.
2. Symbols: those shown in Figure 3.
3. Functions: those depicted in Figure 4.

Figure 3: Variables: stoicheia (triangles) and Platonic solids for the four elements (from left to right): tetrahedron, hexahedron, octahedron, and icosahedron.

Figure 4: Functions (arrows) from stoicheia to the faces of polyhedra, and from there to polyhedra (shapes are not in the same scale).

Plato’s conversion of elements into each other (water into air, fire into air, etc.) is susceptible of framing in the mathematical way of thinking:

Variables: fire, air, earth, and water.

Symbols: those depicted in Figure 3 (bottom polyhedra).

Functions: those shown in Figure 5.

Figure 5: Functions (arrows) relating variables. For each function its corresponding inverse exists, pointing into the reverse direction.

2.2 Geoffroy’s affinity table

Following Cartesian philosophy, in 17^th-century France several scholars developed the vision of a rational, mathematized chemical knowledge. For instance, Bernard le Bovier de Fontenelle (1657-1757), the secretary of the Académie des Sciences since 1697, claimed in his introduction to the Histoire de l’Académie that for some time mathematics had not only yielded an infinity of its own kind of truths, but also produced in the minds quite generally a habit of exactitude and precision even more precious than all these truths (Fontenelle 1970). He suggested the idea of mathematizing chemistry as done in geometry, to be able to make predictions:

If one could reduce chemistry, & general physics to a few universal formula which contain all possible cases, as one reduces the most sublime Questions of modern Geometry, one would be in a state of predicting the changes which would respond to the different suppositions one would like to make, & often one would see quite easily the changes in the suppositions produce quite great variations in the effects. But physics is too vast, & too little known, at least until now, & experiment alone teaches us what is the power of circumstances in varying the phenomena. [Fontenelle as quoted by Kim 2003, p. 78-9]

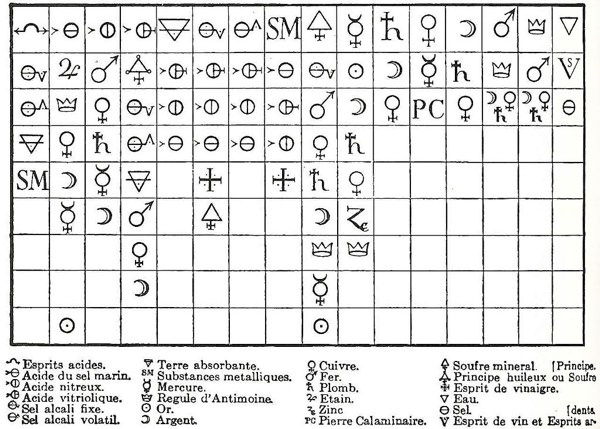
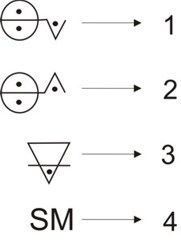
The underlying program was to legitimate chemistry as the theoretical counterpart of ‘vulgar pharmacy’ and as a worthy companion of the physicians’ art (Kim 2003, p. 18). Part of this group was Etienne-François Geoffroy (1672-1731), who introduced the Table des differents rapports observés entre differentes substances (Figure 6). Geoffroy wanted a table in which one could see ‘at a glance’ the different rapports (relations) of the "principal matters one is accustomed to work on in chemistry" (ibid., p. 135). The table soon became not only a collection of information but also a tool for predicting salts and their chemical reactions.

The rule for interpreting the table is as follows: (i) the top row has different substances customarily employed in 17^th-century chemistry; (ii) below each of them, different substances are ordered according to their strength of affinity regarding the top substance. Taking the first column (left hand side), it is headed by acid spirits, which are followed by fixed alkali salt, volatile alkali salt, absorbent earth and metallic substances. This column shows that fixed alkali salt reacts more favorably with acid spirits than the other substances down the column and that it displaces all the substances below it from their existing combination with acid spirits. Moreover, the column tells that volatile alkali salt displaces absorbent earth and metallic substances from their combinations with acid spirits but does not displace fixed alkali from its combination with acid spirits. It is clear that Geoffroy established an order among substances based upon their reactivity with reference to a substance (top of the column).[9] The importance of the chemical context, or better the relational one,[10] is also highlighted in the table, e.g. in the second column headed by acid of marine salt, silver reacts more favorably with the acid in question than mercury. This behavior contrasts with that in a different context, say nitrous acid (third column), where the order is reversed and mercury reacts more favorably with nitrous acid than silver (Kim 2003, p. 136).

The predictive potential of the table was explored by Geoffroy himself, when preparing corrosive sublimate (ibid., p. 137). Although the table showed several drawbacks in the explanation of some chemical experiments (ibid., p. 139), it constitutes an early attempt to use chemical patterns to make predictions.

Geoffroy’s table is framed in the mathematical way of thinking as follows:

1. Variables: chemical substances customarily employed in the 17^th century.
2. Symbols: those depicted in Figure 6.
3. Functions: the order relationships depicted in each column of Figure 6. Figure 7 shows an example of these functions, applied to the first column of Figure 6.

Figure 7: Order relation of the substances depicted in the left-hand-side column of Figure 6 regarding their affinities towards acid spirits (top of the column); 1 indicates the greatest affinity, 4 the lowest one.

2.3 Lavoisier and a language for chemistry

In the Discours Préliminaire of his Traité élémentaire de chimie (1789), Antoine-Laurent de Lavoisier (1743-1794) quoted Étienne Bonnot de Condillac:

We think only through the medium of words. Languages are true analytical methods. Algebra, which is adapted to its purpose in every species of expression, in the most simple, most exact, and best manner possible, is at the same time a language and an analytical method. The art of reasoning is nothing more than a language well arranged. [Lavoisier 1965, p. xiii]

This can be regarded a summary of Lavoisier’s work in nomenclature for chemistry, which turned out to be a language that allowed classifying substances into chemical elements and their compounds. In Lavoisier’s scheme, oxygen played an important role: all metals yielded oxides in combination with it, while acids were obtained from oxygen’s combination with nonmetals. Hence, a new hierarchy of substances appeared, element-oxygen compounds. Members of each of these two latter classes combined to yield salts. An example of the classification and the relation of classes found by Lavoisier is magnesium sulphate. Let us have magnesium, a metal, and sulphur, a nonmetal; magnesium reacts with oxygen to form magnesium oxide and sulphur yields sulphuric acid by reacting with oxygen. Magnesium oxide and sulphuric acid form magnesium sulphate. A generalization of this is: Let E, M, nM, Ox, A and Sl be the set of chemical elements, metals, nonmetals, oxides, acids, and salts, respectively; and let O, Mg, S, MgO, SO₃ and MgSO₄ be oxygen, magnesium, sulphur, magnesium oxide, sulphuric acid, and magnesium sulphate, respectively. Thus,[11] E = M ∪  nM ∪  O, Mg ∈  M, S ∈  nM and then Mg + O →  MgO ∈  Ox, S + O →  SO₃ ∈  A and MgO + SO₃→ MgSO₄ ∈  Sl. A further generalization is the following: E = M ∪  nM ∪  O, M + O →  M_xO_y ∈  Ox, nM + O →  nM_jO_k ∈ A, MO + nMO →  s ∈  Sl; which can be regarded as the basis for an algebra.

To frame Lavoisier’s work above in terms of Weyl’s steps for mathematical thinking, we write the following:

1. Variables: chemical elements, oxides, acids, and salts.
2. Symbols: alchemical symbols like those used in Figure 6.
3. Functions: {chemical elements of the 18^th century} → {M, nM, O}; {M, O} →  M_xO_y ∈  Ox, with x, y ∈ N (natural numbers); {nM, O} → nM_jO_k ∈ A, with j, k ∈ N; {M_xO_y, nM_jO_k} → s ∈ Sl. In all cases, → indicates a function.[12]

Lavoisier was not far from actually formulating algebraic equations and, therefore, from leaving instances of functional thinking. When studying the acidification of metals, he wrote: "Let any metallic substance be S M, let any acid be [], let water be ∇ [...] Then, we will have, for the general expression of any metallic solution [Metallic solution =] (S M) (∇ )" (Lavoisier 1782, p. 515) where S M and are independent variables. It is likely, according to Gillispie (1960, p. 243), that Lavoisier worked on a mathematization of chemistry because of the influence several mathematicians had upon him, for example Laplace, with whom Lavoisier worked on the quantification of heat exchanges in chemical processes. Regarding algebra, Lavoisier stated: "Algebra is the analytic method per excellence: It has been contrived to facilitate the operations of the understanding, to make reasoning more concise, and to contract into a few lines what we would have needed many pages of discussion" (as quoted by Swetz 1994, p. 97). The scientific interest was reciprocal between Lavoisier and his mathematical colleagues. According to Cajori (1991, p. 256): "Through A. L. Lavoisier he [Lagrange] became interested in chemistry, which he found ‘as easy as algebra’." An example of Lavoisier’s mathematical spirit is his way of expressing the law of conservation of matter: "We must lay it down as an incontestable axiom that in all the operations of art and nature, nothing is created, an equal quantity of matter exists both before and after the experiment" (as quoted by Gillispie 1960, p. 231).

2.4 Mendeleev’s periodic table

Another example of the relationship between mathematics and chemistry is the 19^th-century treatment of chemical elements by several scientists. In 1817 Johann Wolfgang Döbereiner developed an arithmetic relationship for chemical elements according to which for some triads of elements, the atomic weight of the element in the middle was roughly the average of those of the other. Periodicity of some properties of the chemical elements regarding atomic weight was first noticed by Alexandre-Emile Béguyer de Chancourtois and John Alexander Reina Newlands as early as 1862-1864 as well as by William Odling and Gustavus Detlef Hinrichs (Scerri 2007, chap. 3). Periodicity became more powerful with Julius Lothar von Meyer and Dmitri Ivanovich Mendeleev,[13] who both predicted new elements based upon the regularities. These trends were condensed in the periodic law by Mendeleev (1834-1907).

Considering the kind of research Mendeleev performed on the set of chemical elements, we can state that, judging from our current mathematical knowledge, he carried out a multivariate analysis of chemical information and in a wise manner was able to reduce such a multidimensional amount of information to a simple law, the periodic law. He processed information regarding reactivities, stoichiometries of chemical compounds, and physical properties; all in all a multidimensional problem.

We have shown that the trends depicted by the periodic table follow a topological structure (Restrepo et al. 2004, 2006a, 2006b, Restrepo & Pachón 2007) and several other authors have shown that different mathematical theories are suitable to treat and reproduce to some extent the structure of trends found by Mendeleev in 1869. Some of these mathematical theories include number theory, information theory, order theory, group theory, and topology (King & Rouvray 2006).

A question to ponder on is the kind of mathematics Mendeleev knew. What kind of mathematics was taught to pupils at Russian schools during Mendeleev’s childhood? Does this mathematics bear any relationship with the treatment he gave to chemical elements?

Mendeleev made use of the mathematical way of thinking when developing the periodic law. Its variables, symbols and functions were the following:

1. Variables: properties of the chemical elements such as atomic weight, valence, acidity, atomic volume, oxidation state, etc.
2. Symbols: he did not assign a symbol to each property but that did not prevent him to develop functions relating the properties to each other.
3. Functions: atomic weight → one of the other properties. Written in modern notation, if we call P a property and A the atomic weight, then P = f(A).

The kind of function Mendeleev found was one relating each atomic weight to a property value. As he claimed: "The properties of the elements (and of the simple and compound substances they form) show a periodic dependence on their atomic weights" (as quoted by Jensen 2005, p. 47). In his Faraday Lecture of 1889, Mendeleev (1889) mentioned the work of Tchitchérin who found simple relationships among atomic volumes (V) at 25 °C, which could be expressed according to V = A(2-0.0053A _* n), A being atomic weight and n an integer. Here is a function between the atomic weight and the atomic volume.

?The periodic table, in turn, can also be framed in Weyl’s mathematical way of thinking. As we have shown, there is a topological structure underlying the periodic table (Restrepo et al. 2004, 2006a, 2006b, Restrepo & Pachón 2007). This study can be summarized as follows:

1. Variables: properties characterizing chemical elements and sets of chemical elements.
2. Symbols: p₁(x), p₂(x),…; p_i being the property i in question; each element x is given by x = (p₁(x), p₂(x),…); contemporary symbols for the chemical elements; set notation for sets of chemical elements.
3. Function: a function from p₁(x), p₂(x),… to the set of chemical elements and another one from the chemical elements to a collection of subsets of chemical elements. The first function characterizes the chemical elements in terms of their properties, the second function is built as a similarity function measuring the resemblance between the properties of the chemical elements (Figure 8).

Figure 8: Function relating properties to chemical elements and elements to classes of elements appearing in the periodic table.

2.5 Cayley and the quest for enumerating alkanes

In 1857 Arthur Cayley (1821-95), a mathematician, developed the mathematical theory of trees (Cayley 1857) where he found a recursive formula for determining the number of rooted trees in terms of its branches (‘edges’ in graph theoretical terms). Later he published a paper in the then leading chemical journal, Berichte der deutschen Chemischen Gesellschaft (Cayley 1875). The paper was on calculating the number of possible alkane isomers that fulfill the formula C_nH_2n+2, and of alkyl radicals fulfilling C_nH_2n+1, with n varying from 1 to 13. Even though, as pointed out by Trinajstić (1997), Cayley did not attain the correct number of alkanes for C₁₂ and C₁₃, and for the C₁₃ alkyl radicals, he was the first to consider, and treat, the problem of calculating related substances with mathematical insight.

His publication in a chemical journal generated a series of contributions by the chemical community. It was the first combinatorial problem in chemistry and eventually culminated in Pólya’s theorem offering the most powerful enumeration method available today to chemists (Pólya 1937).[14]

Cayley’s steps of Weyl’s mathematical thinking are the following:

1. Variables: the number of carbon atoms in alkanes and alkyl radicals, the number of bonds (‘bands’ in Cayley’s terms), and the number of rooted trees.
2. Symbols: n (number of carbon atoms), t (number of rooted trees).[15]
3. Function: n → t

After developing a mathematical formalism to calculate the number of molecular structures for alkanes and alkyl radicals that fulfil carbon tetravalence, Cayley extended the problem to calculate the number of molecular structures fulfilling di- and trivalence, such as oxygen- and boron-trees.[16]

2.6 Sylvester’s algebra and chemistry

James Joseph Sylvester (1814-97) was a 19^th-century leading mathematician with an interest in chemistry. He wrote two influential papers related to chemistry in 1878 (Sylvester 1878a, b) in which he developed an analogy between algebra and chemistry. His algebra deals with the irreducible forms associated to binary quantics, i.e. "Any binary quantic may be denoted by a single letter with a number attached corresponding to its degree, and may therefore be adumbrated by a chemical symbol with corresponding valence" (Sylvester 1878a). The number of factors of each binary quantic is analog to the number of bonds (valences) of an atom in a molecule, e.g. a linear form is a 1-valence atom, a quadratic form a 2-valence atom and so on (Sylvester 1878b).

For him "an invariant of a system of binary quantics of various degrees is the analogue of a chemical substance composed of atoms of corresponding valences" (Sylvester 1878b). The order of those invariants, taken for each set of coefficients, corresponds to the number of atoms of the respective valence. Such as the valence of atoms were supposed to be invariant under chemical reactions, such were the binary quantics invariant under several mathematical operations. His idea of relating mathematical invariance to invariance in chemistry was related to the identity of atoms in molecules.

Sylvester also found that the weight of the invariant (set of atoms) corresponds to the number of bonds in what he called ‘chemicographs’. Hence, he concluded that "every invariant […] thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph" (Sylvester 1878b). He established a mapping between the set of invariants (atoms of certain valence) with a graph, which corresponded to the chemical representation of atoms linked by bonds. Apart from the mathematical discussion, the quotation above is famous in the history of mathematical chemistry and graph theory, because it was the first use of the terms ‘chemicograph’ and ‘graph’, in this sense, at least in print.

Sylvester was so enthusiastic about the analogy between algebra and chemistry he had found that he finally claimed: "Thus we see that chemistry is the counterpart of a province of algebra as probably the whole universe of fact is, or must be, of the universe of thought" (Sylvester 1878a).

Sylvester’s algebraic findings for chemistry can be framed in Weyl’s mathematical way of thinking as follows:

1. Variables: atoms of a molecule, their valences, and chemicographs.
2. Symbols: chemical element symbols and N (natural numbers indicating valences).
3. Function: {(chemical element symbols, valences)} → chemicograph, which is the couple made of the set of chemical element symbols of all atoms in the molecule and the bonds of those atoms, expressed as couples of chemical element symbols.

2.7 Wiener, from structure to macroscopic properties

In 1947 Harry Wiener (1924-98) published an important paper for the relationship between chemistry and mathematics, which showed how to relate the molecular structure associated to alkanes with their boiling points (Wiener 1947). Wiener considered a molecular structure as a graph in mathematical terms[17] and searched for graph features that yield estimated boiling points. John Platt, a famous quantum chemist of the time, realized the importance of Wiener’s pioneering work and tried to analyze and interpret its physical meaning (Platt 1952). Platt had already written many milestone papers and monographs on quantum chemistry and the classification and nomenclature of UV spectra of benzenoid hydrocarbons, but his paper on Wiener’s work did not receive the deserved credit (Hosoya 2002). Although the value of Wiener paper was not recognized immediately, his work over time went into the so-called Wiener index, the first of hundreds of ways to extract real numbers from chemical graphs; indices of this sort have been called molecular descriptors (Todeschini & Consonni 2000, p. 303). Currently, it is accepted that the Wiener index is related to molecular branching and is one of the indices of major use in studies that estimate substances properties based upon molecular structure.

Graph theory is a mathematical field started by Euler in 1736 (Biggs et al. 1986, chap. 1). Graphs were the root of Cayley’s work on the calculation of possible alkanes and also the starting point for the analogy Sylvester found between chemistry and algebra. Wiener’s work was the first one in which graphs were mathematically operated with the aim of relating them to macroscopic properties of chemical substances, an idea which is investigated in the currently exploding subfield of mathematical chemistry called QSAR or more generally QSPR (Quantitative Structure-Activity Relationships and Quantitative Structure-Property Relationships, respectively).

The steps followed by Wiener in his mathematical way of thinking were:

1. Variables: the boiling point of alkanes, "number of pairs of carbon atoms which are separated by three carbon-carbon bonds" (Wiener 1947) and the "sum of the distances between any two carbon atoms in the molecule, in terms of carbon-carbon bonds" (Wiener 1947).
2. Symbols: T_B, p and w for the three variables mentioned before.
3. Function: T_B = aw + bp + c, where a, b, and c are constants for a given isomeric group of alkanes.

Having discussed the mathematical association between molecules and graphs that Sylvester found, it can be stated that Wiener went beyond, by taking the molecular graph and associating to it two variables, i.e. p and w. In this sense, the very process of extracting p and w from the graph is again guided by a mathematical way of thinking, which can be stated as follows:

1. Variables: molecular structure (graph), "number of pairs of carbon atoms which are separated by three carbon-carbon bonds" (Wiener 1947) and "sum of the distances between any two carbon atoms in the molecule, in terms of carbon-carbon bonds" (Wiener 1947).
2. Symbols: (A, B) for a graph and p and w for the two variables mentioned before.[18]
3. Function: (A, B) → {p, w}.

3. Conclusions

We showed seven cases of mathematical thinking to address chemical questions. Our aim was to discuss how they fit Weyl’s conception of mathematical thinking, i.e. setting up variables, looking for symbols for them and finding functions relating the variables to each other. The mathematical thinking we found does not imply that the authors in question were aware of that. It is from the present perspective that we analyzed those works and found they can be reformulated in Weyl’s mathematical way of thinking.

Plato’s variables were geometrical; they condense abstractions of the daily transformations observed in nature. A first function for Plato goes from triangles to polyhedra, from stoicheia to the four elements of ancient Greek philosophy of nature. A second function arises by relating polyhedra. It is here where Plato’s mathematical thinking is followed to its last consequences: only those transformations allowed by geometry are realizable, all others are forbidden and not happening in nature.

As Mendeleev recalled (Jensen 2005, p. 163), it was the wealth of chemical information and the need of giving sense to it, which prompted him, as well as Geoffroy, to find patterns in the information they had at hand. In Geoffroy’s case this led to the first affinity table, in Mendeleev’s case to the periodic law and the periodic table. Geoffroy ordered chemicals according to affinity, relating substances with ordinal numbers. Mendeleev’s functional thinking took properties of the chemical elements and related them to atomic weight, which led to the periodic law. A second instance of his mathematical thinking is found in the periodic table, where the function goes from the set of properties to the set of chemical elements and from it to a collection of its subsets, which are built up by looking for similarities among chemical elements.

Lavoisier’s classification of substances and his later relation between classes fit with Weyl’s mathematical way of thinking too. His work allows generality for chemistry, because once an element is classified as metal or nonmetal, one can predict its behavior with oxygen to produce oxygenated products. From those products, in turn, one can make predictions about salts. Hence, belonging to a class allows predicting its chemical behavior.

Cayley’s and Sylvester’s works, at first glance, are easily framed in the mathematical way of thinking, because both scientists were mathematicians. However, being able to understand problems and raising questions from other disciplines is remarkable. Cayley and Sylvester both bridged mathematics and chemistry. Cayley, specially, founded a new field, the calculation of possible molecular structures by the assistance of mathematics, which is continued in contemporary mathematical chemistry. Both scientists took molecular drawings, commonly used in chemistry, and translated them into mathematics, thereby inducing a multitude of mathematical and chemical interpretations. Part of that was Wiener’s work, relating molecular structures (drawings) to macroscopic properties of the substances associated to those structures.

Cayley’s function went from the number of carbons in alkanes and alkyl radicals to the number of rooted trees. Sylvester proved the connection between molecular drawings representing molecular structures and molecular graphs. In so doing, he showed that having chemical information at hand, such as the kind of elements in a chemical substance and their valences, a function can be set up to relate that information to the elements of the sets of graphs.

In Cayley’s and Sylvester’s legacy, Wiener went further in showing that drawings of chemical structures are something else than graphical representations of molecules, they are full of mathematical flavor and can be explored in that sense. His relation between mathematical descriptors (e.g. p and w) derived from molecular graphs and properties measured in chemical laboratories was pioneering and stimulated the search for other functions from molecular descriptors to macroscopic properties, one of the most rapidly growing fields in discrete chemomathematics.

These seven examples of mathematical thinking when pondering on chemical questions illustrate its long tradition in chemistry before the 20^th century. It is worth noting that there are different degrees of mathematical thinking in chemistry and of ways in which it can be found, when one looks for it.

Acknowledgements

G. Restrepo thanks the Universidad de Pamplona for the financial support to conduct this research. The authors thank Alan Rocke and Joachim Schummer for their valuable comments and suggestions on the first drafts of this paper.

Notes

[1]  MATCH Communications in Mathematical and in Computer Chemistry (MATCH), Journal of Mathematical Chemistry (JOMC), and Iranian Journal of Mathematical Chemistry (IJMC).

[2]  http://www.iamc-online.org/index.htm.

[3]  According to Hamley 1934, p. 9: "The word ‘variable’ seems to have been first used by Leibniz, who wrote, in the introduction to his Analyse: Those quantities are called variable which continually increase or diminish and on the contrary those are constant, which remain the same while others change".

[4]  Hamley (1934, p. 11) stated that Weierstrass was the first to link variables to symbols: "A […] variable is a symbol which represents the different elements of an assemblage […]. Each of these elements is one of the values which the variable can take".

[5]  Hamley (1934, p. 13) stated that the term ‘function’ was coined by Leibniz.

[6]  Following Weyl 1940, one can see the advantage of using symbols, for example, when dealing with quantities. Having three stones (labeled ‘3’), independent of their individual shapes, colors, weights, etc., it is clear that those stones are more in number than having just one rough-red-heavy stone (labeled ‘1’). The importance of symbols ‘1’ and ‘3’ is that 1 is lower than 3, it does not really matter whether the stones are of a particular color, or if the stone labeled ‘1’ is bigger than the three labeled ‘3’. Hence, ‘1’ and ‘3’ carry cardinality information that leads to an order relationship between them.

[7]  Stoicheia is the plural of stoicheion, which meant the smallest part of something, an element, a little piece (Versteegh 1977).

[8]  All these manifestations of tetrahedra are grouped by Plato in the element fire (Timaeus, 58c).

[9]  In mathematical terms, what Geoffroy found was a local order for a collection of substances (those gathered in each column of his table).

[10]  Schummer (1998) has stated that the chemical context is essentially a relational context, where the chemical behavior of substances is determined by other substances.

[11]  Set theoretical symbols used here are ∪ for union, and ∈ for being an element of.

[12]  Brackets {} indicate a set.

[13]  Meyer indicated that there should be an element of atomic weight greater than that of silicon by a difference of 44.55, which later was found to be Germanium. Mendeleev predicted several properties of what was afterwards known as Germanium, Gallium, and Scandium (Scerri 2007, chapter 3).

[14]  Currently, tree counting formulas are used in computer science to estimate running times in the design of algorithms (Rosen 2000, p. 622).

[15]  Cayley did not use t to symbolize the number of rooted trees, but searching for concrete values of such a variable is the aim of his paper (Cayley 1875). Regarding symbols, Cayley stated in his paper: "It should be observed that the tree-symbol of the paraffin is completely determined by means of the tree formed with the carbon-atoms, or say of the carbon-tree, and that the question of the determination of the theoretic number of the paraffins C_nH_2n+2 is consequently that of the determination of the number of the carbon-trees of n knots, viz. the number of trees with n knots, subject to the condition that the number of branches from each knot is at most = 4" (Cayley 1875).

[16]  For example, structures of the family B_nH_n+2 (Cayley 1875).

[17]  A graph is a couple (V, E) of vertices V and edges E. In chemistry V is usually a set of atoms and E a set of bonds.

[18]  Wiener did not use this symbol, which is the customary representation of graphs in mathematical terms.

References

Biggs, N.; Lloyd, E. & Wilson, R.: 1986, Graph Theory, 1736-1936, Oxford University Press, New York.

Cajori, F.: 1991, A History of Mathematics, Chelsea, New York.

Cayley, A.: 1857, ‘On the theory of the analytical forms called trees’, Philosophical Magazine, 13, 172-6.

Cayley, A.: 1875, ‘Ueber die analytischen Figuren, welche in der Mathematik Bäume genannt werden und ihre Anwendung auf die Theorie chemischer Verbindungen’, Berichte der deutschen chemischen Gesellschaft, 8, 1056-9. (English version: ‘On the analytical forms called trees, with application to the theory of chemical combinations’, Report of the British Association for the Advancement of Science, 257-305).

Doumas, L.A.A. & Hummel, J.E.: 2005, ‘Approaches to modeling human mental representations: what works, what doesn’t, and why’, in: K.J. Holyoak & R.G. Morrison (eds.), The Cambridge Handbook of Thinking and Reasoning, Cambridge University Press, Cambridge.

Fontenelle, B.B.: 1970, ‘Preface to the History of the Academy of Sciences, from 1666 to 1699’, in: The achievement of Bernard le Bovier de Fontenelle, Johnson, New York, part IV, pp. 17-23.

Gillispie, C.C.: 1960, The Edge of Objectivity, Princeton University Press, Princeton.

Hamley, H.R.: 1934, Relational and Functional Thinking in Mathematics, National Council of Teachers of Mathematics, Washington, DC.

Hosoya, H.: 2002, ‘The topological index Z before and after 1971’, Internet Electronic Journal of Molecular Design, 1, 428-42.

Jensen, W.B.: 2005, Mendeleev on the Periodic Law: Selected Writings, 1869-1905, Dover, New York.

Kim, M.G.: 2003, Affinity, That Elusive Dream, MIT Press, Cambridge.

King, B. & Rouvray, D.H.: 2006, The Mathematics of the Periodic Table, Nova, New York.

Lavoisier, A.L.: 1782, ‘Considérations générales sur la dissolution des metaux dans les acides’, Mémoires de l’Académie des Sciences, p. 516.

Lavoisier, A.L.: 1965, Elements of Chemistry, Dover, New York.

Lloyd, D.R.: 2007, ‘The chemistry of Platonic triangles: problems in the interpretation of the Timaeus’, Hyle – International Journal for Philosophy of Chemistry, 13, 99-118.

Mendeleev, D.I.: 1889, ‘The periodic law of the chemical elements’, Journal of Chemical Society, 55, 634-56 [http://web.lemoyne.edu/~giunta/mendel.html].

Platt, J.R.: 1952, ‘Prediction of isomeric differences in paraffin properties’, Journal of Physical Chemistry, 56, 328-36.

Pólya, G.: 1937, ‘Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen’, Acta Mathematica, 68, 145-254.

Restrepo, G.; Mesa, H.; Llanos, E.J. & Villaveces, J.L.: 2004, ‘Topological study of the periodic system’, Journal of Chemical Information and Computer Sciences, 44, 68-75.

Restrepo, G.; Llanos, E.J. & Mesa, H.: 2006a, ‘Topological space of the chemical elements and its properties’, Journal of Mathematical Chemistry, 39, 401-16.

Restrepo, G.; Mesa, H.; Llanos, E.J. & Villaveces, J.L.: 2006b, ‘Topological study of the periodic system’, in: B. King & D.H. Rouvray (eds.), The Mathematics of the Periodic Table, Nova, New York, pp. 75-100.

Restrepo, G. & Pachón, L.: 2007, ‘Mathematical aspects of the periodic law’, Foundations of Chemistry, 9, 189-214.

Restrepo, G. & Villaveces, J.L.: 2012, ‘Discrete mathematical chemistry, a social perspective of its emergence and reception’, Hyle – International Journal for Philosophy of Chemistry, forthcoming.

Rosen, K.H.: 2000, Handbook of Discrete and Combinatorial mathematics, CRC Press, Boca Raton.

Scerri, E.: 2007, The Periodic Table: Its Story and Its Significance, Oxford University Press, New York.

Schummer, J.: 1998, ‘The chemical core of chemistry I: a conceptual approach’, Hyle – International Journal for Philosophy of Chemistry, 4, 129-162.

Swetz, F.J.: 1994, Learning Activities from the History of Mathematics, Weston Walch, Portland.

Sylvester, J.J.: 1878a, ‘On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, with three appendices’, American Journal of Mathematics, 1, 64-125.

Sylvester, J.J.: 1878b, ‘Chemistry and algebra’, Nature, 17, 284.

Todeschini, R. & Consonni, V.: 2000, Handbook of Molecular Descriptors, Wiley-VCH, Weinheim.

Trinajstić, N.: 1997, ‘Mathematics and chemistry – the unlikely partners’, in: D.H. Rouvray (Ed.), Concepts in Chemistry: A Contemporary Challenge, Research Studies Press, Somerset.

Versteegh, C.H.M.: 1977, Greek Elements in Arabic Linguistic Thinking, Brill, Leiden.

Weyl, H.: 1940, ‘The mathematical way of thinking’, Science, 92, 437-46.

Wiener, H.: 1947, ‘Structural determination of paraffin boiling points’, Journal of the American Chemical Society, 69, 17-20.

Guillermo Restrepo:
Interdisciplinary Research Institute, Universidad de Pamplona, Bogotá, Colombia & Laboratorio de Química Teórica, Universidad de Pamplona, Pamplona, Colombia; guillermorestrepo@gmail.com

José L. Villaveces:
Grupo de Química Teórica, CEIBA, Complex Systems Research Center, Universidad de los Andes, Bogotá, Colombia